Содержание
- 2. Ключевые вопросы лекции Что такое множество и какие существуют операции над множествами? Какие бывают отношения и
- 3. План уроков темы Описание множеств. Операции над множествами. Отношения. Свойства отношений. Функция. Отображение. Операции. Алгебраические системы
- 4. Множества Множество – совокупность любых объектов, называемых элементами множества. Примеры множеств: множество жителей данного города, множество
- 5. Способы задания множеств 1) Перечислением всех элементов A = {Петр, Сергей, Юлия, Ольга} B={1,3,5,7,9}
- 6. Способы задания множеств
- 7. Способы задания множеств
- 8. Сравнение множеств Множество А называется подмножеством множества В, если все элементы А содержатся в В. Два
- 9. Сравнение множеств
- 10. Алгебра множеств
- 11. Операции над множествами Основные операции, определяемые над множествами: Пересечение : A ∩ B := { x
- 12. Операции над множествами. Примеры Пусть А={К, А, Т, Я}, В={Н, И, К, О, Л, А, Й}
- 13. Свойства операций над множествами 1) Коммутативность. 5) Свойство единицы 2) Ассоциативность. 6) Закон поглощения 3) Дистрибутивность.
- 14. Декартово произведение Декартово или прямое произведение: A × B = { ( a , b )
- 15. Декартово произведение Декартово или прямое произведение: A × B = { ( a , b )
- 16. План уроков темы Описание множеств. Операции над множествами. Отношения. Свойства отношений. Функция. Отображение. Операции. Алгебраические системы
- 17. Отношения
- 18. Отношения
- 19. Способы задания отношения
- 20. Способы задания отношения
- 21. Способы задания отношения
- 22. Способы задания отношения Графический способ задания отношений M = {Петр, Сергей, Мирон, Юлия, Ольга} R =
- 23. Матрица бинарного отношения M = {Петр, Сергей, Мирон, Юлия, Ольга} R = {(Петр, Юлия), (Юлия, Петр),
- 24. Свойства бинарного отношения
- 25. Свойства бинарного отношения
- 26. Свойства бинарного отношения
- 27. Свойства бинарного отношения
- 28. Свойства бинарного отношения
- 29. Отношения эквивалентности
- 30. Отношения эквивалентности Ключевое свойство отношения эквивалентности: множество A разбивается на непересекающиеся классы эквивалентности, элементы внутри такого
- 31. Отношения порядка Связное (полное) отношение – отношение R, в котором для любой пары a,b из условия
- 32. Отношения порядка
- 33. Отношения порядка Связное (полное) отношение – отношение R, в котором для любой пары a,b из условия
- 34. Применение отношений Описание смысла подмножеств R = {(Петр, Юлия), (Юлия, Петр), (Мирон, Ольга), (Ольга, Мирон), (Сергей,
- 35. Применение отношений
- 36. Применение отношений
- 37. План уроков темы Описание множеств. Операции над множествами. Отношения. Свойства отношений. Функция. Отображение. Операции. Алгебраические системы
- 38. Соответствие
- 39. Соответствие Область определения соответствия Р (обозначается D(P)) – множество таких a, для которых существует образ. Область
- 40. Виды соответствий Всюду определенное соответствие : D(P) = A. В противном случае соответствие называется частичным. Сюръективное
- 41. Виды соответствий Инъективное соответствие (инъекция) – соответствие, при котором прообразом любого элемента из множества E(P) является
- 42. Виды соответствий Взаимнооднозначное соответствие – соответствие, которое функционально и инъективно. Биекция (1-1 соответствие) – соответствие, которое
- 43. Алгебраические операции
- 44. Бинарная операция
- 45. Свойства (типы) бинарных операций
- 46. Нулевой элемент Элемент 0 множества A называют левым (правым) нулем относительно данной операции ∗ , если
- 47. Нейтральный элемент Элемент e множества A называют левым (правым) нейтральным элементом относительно операции (∗), если e∗a=a
- 48. Алгебраические операции Пусть ∗ - бинарная операция на множестве A, обладающая нейтральным элементом e . Элемент
- 49. План уроков темы Описание множеств. Операции над множествами. Отношения. Свойства отношений. Функция. Отображение. Операции. Алгебраические системы
- 50. Алгебраические структуры Опр. Непустое множество А, вместе с одной или несколькими алгебраическими операциями, определенными на этом
- 51. Алгебраические структуры (АС) Опр. Непустое множество А, вместе с одной или несколькими алгебраическими операциями, определенными на
- 52. Группоид Опр. Непустое множество А, в котором определена только одна бинарная операция, называется группоидом. В группоиде
- 53. Полугруппа Опр. Непустое множество А, в котором определена только одна бинарная операция, называется группоидом. В группоиде
- 54. Моноид Опр. Полугруппа А, в которой существует единичный элемент, называется полугруппой с единицей, или моноидом. Примеры:
- 55. Группа Опр. Моноид G, в котором для любого элемента существует симметричный или противоположный элемент, называется группой.
- 56. Абелева группа Опр. Группа ( G , ∗ ) называется абелевой, если операция ∗ в ней
- 57. Абелева группа Опр. Группа ( G , ∗ ) называется абелевой, если операция ∗ в ней
- 58. Свойства групп Утверждение 1. Нейтральный элемент единственен: Если e1 , e2 — нейтральные, то e1* e2
- 59. Свойства групп Утверждение 3. Верны законы сокращения: c * a = c * b ⇔ a
- 60. Свойства групп Обратный элемент к нейтральному есть сам нейтральный элемент: e − 1 = e. (
- 61. АС с двумя операциями: кольцо
- 62. Кольцо многочленов Тема: Введение в общую алгебру --------------------------------------- Кольцо многочленов — кольцо, образованное многочленами от одной
- 63. АС с двумя операциями: поле
- 65. Скачать презентацию






























































 Розв'язання задач
Розв'язання задач Уравнение Х2=a
Уравнение Х2=a Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность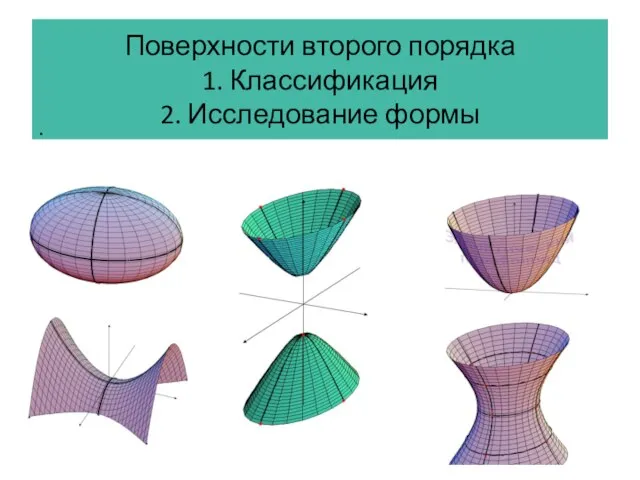 Поверхности второго порядка
Поверхности второго порядка Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств Идеально сбалансированное дерево. Задание
Идеально сбалансированное дерево. Задание Десятичные дроби. Выполнить действия
Десятичные дроби. Выполнить действия Линейные уравнения. Ярмарка по решению старинных русских задач
Линейные уравнения. Ярмарка по решению старинных русских задач Проценты. ОГЭ и ЕГЭ
Проценты. ОГЭ и ЕГЭ Юный математик
Юный математик Элементы комбинаторики
Элементы комбинаторики Теорема Пифагора
Теорема Пифагора Линейное программирование. Графический метод
Линейное программирование. Графический метод Таблица значений синуса, косинуса, тангенса для углов
Таблица значений синуса, косинуса, тангенса для углов Таблица сложения
Таблица сложения Станция Игровая. Занимательная математика
Станция Игровая. Занимательная математика Вероятность распределения случайных чисел
Вероятность распределения случайных чисел Многогранники. 5 класс
Многогранники. 5 класс Lektsia_5
Lektsia_5 Сечения куба плоскостью
Сечения куба плоскостью Умножение
Умножение Путешествие в страну математики. Дидактическая игра Веселые цифры
Путешествие в страну математики. Дидактическая игра Веселые цифры Измерение ёмкости (вместимости). 3 класс
Измерение ёмкости (вместимости). 3 класс 13_razn_dejstv_1
13_razn_dejstv_1 Конус
Конус Простейшие задачи. Теоретический тест в координатах. 9 класс
Простейшие задачи. Теоретический тест в координатах. 9 класс Описанная и вписанная окружности треугольника
Описанная и вписанная окружности треугольника Симметрия. Симметрия относительно точки
Симметрия. Симметрия относительно точки