Слайд 2ПРЯМАЯ ЭЙЛЕРА
Центроид треугольника (центр тяжести треугольника) — точка пересечения медиан в треугольнике
Ортоцентр
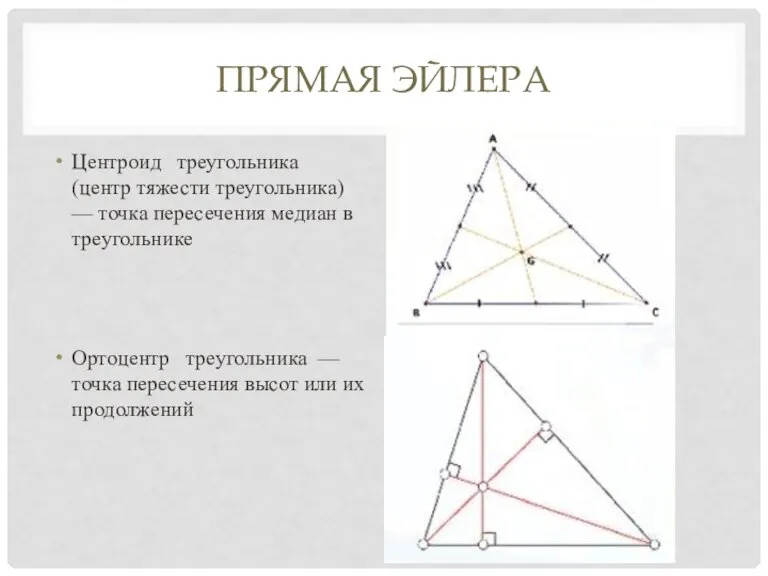
треугольника — точка пересечения высот или их продолжений
Слайд 3ПРЯМАЯ ЭЙЛЕРА( ТЕОРЕМА )
В любом треугольнике центр описанной окружности, центроид и ортоцентр

лежат на одной прямой, эту прямую называют прямая Эйлера.
р – прямая Эйлера
Слайд 4ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О ПРЯМОЙ ЭЙЛЕРА. ШАГ 1
Рассмотрим треугольник АВС.
Проведем в нем высоты.
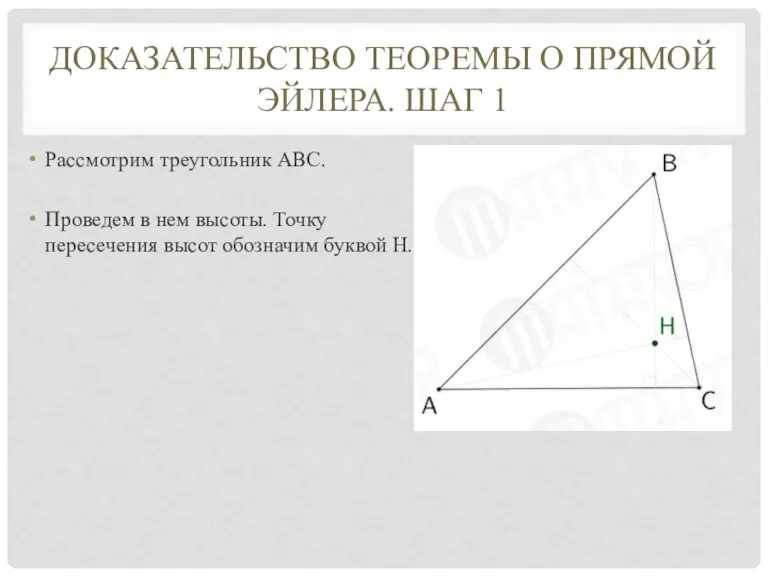
Точку пересечения высот обозначим буквой Н.
Слайд 5ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О ПРЯМОЙ ЭЙЛЕРА. ШАГ 2
Опишем вокруг треугольника окружность с центром

в точке О.
Слайд 6ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О ПРЯМОЙ ЭЙЛЕРА. ШАГ 3
Проведем медиану ВР.
Пусть отрезок ОН пересекает

медиану ВР в точке М.
Рассмотрим треугольники РОМ и ВНМ.
OP⊥AC так как O— центр описанной окружности, который лежит на пересечении серединных перпендикуляров;
AP=PC по условию: значит OP – серединный перпендикуляр;
BH⊥AC -по условию. Из перпендикулярности двух прямых к одной прямой, следует: ОР||BH
Из параллельных прямых, следует, что их накрест лежащие углы равны: ∠О= ∠H
∠OMP= ∠BMH - как вертикальные
треугольник POM ~ треугольнику BHM по двум углам. Из подобия треугольника следует ВМ/МР =ВН/OP
По лемме о центре описанной окружности, ортоцентре и середине стороны треугольника:
BH=2*OP или ВН/ОР=2 отсюда ВМ/МР=2/1
Слайд 7ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О ПРЯМОЙ ЭЙЛЕРА. ШАГ 4
Таким образом получаем, что точка М,
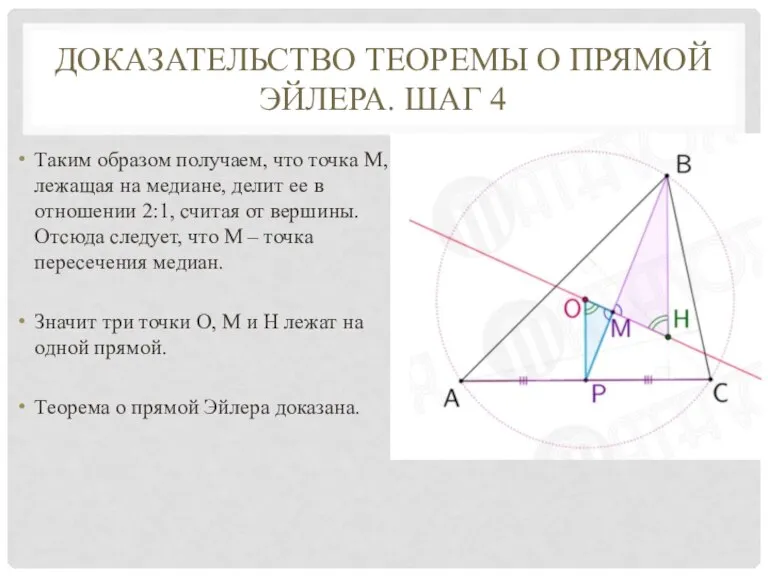
лежащая на медиане, делит ее в отношении 2:1, считая от вершины. Отсюда следует, что М – точка пересечения медиан.
Значит три точки О, М и Н лежат на одной прямой.
Теорема о прямой Эйлера доказана.
Слайд 8ЛЕММА ИЗ ТЕОРЕМЫ ЭЙЛЕРА
Если H-ортоцентр треугольника ABC, OM1 - перпендикуляр, опущенный из

центра O описанной окружности на сторону BC, то AH = 2OM1
Слайд 9ДОКАЗАТЕЛЬСТВО ЛЕММЫ ИЗ ТЕОРЕМЫ ЭЙЛЕРА
1) Через каждую высоту треугольника ABC проведем

прямую, параллельную противолежащей стороне. Получим треугольник A 1B1C1
2) Так как два угла опираются на одну и ту же дугу, то ∠ B1HC1 = 2∠B1A1C1 . Углы BAC и B1A1C1 равны как противолежащие углы параллелограмма ABA1C, поэтому ∠ BOC = 2∠BAC=2∠B1A1C1 = ∠B1HC 1.
3) Так как B1C1 =2BC, то равнобедренные треугольники COB и B1HC1 подобны с коэффициентом подобия 2
4) Так как отрезок AH и OM1 - соответственны высотам подобных треугольников, то AH = 2OM 1 . Что и требовалось доказать: AH = 2OM 1
Доказательство леммы из теоремы Эйлера
Слайд 10ЗАДАЧА №1
Дано :треугольник ABC, точка M – центроид, O – центр вписанной
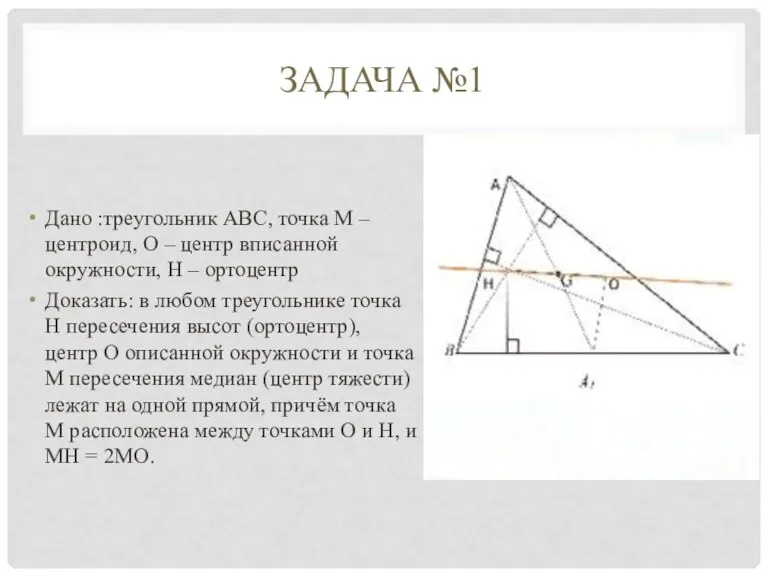
окружности, H – ортоцентр
Доказать: в любом треугольнике точка H пересечения высот (ортоцентр), центр O описанной окружности и точка M пересечения медиан (центр тяжести) лежат на одной прямой, причём точка M расположена между точками O и H, и MH = 2MO.
Слайд 11ЗАДАЧА №2
остроугольном треугольнике ABC высоты пересекаются в точке H, а медианы —
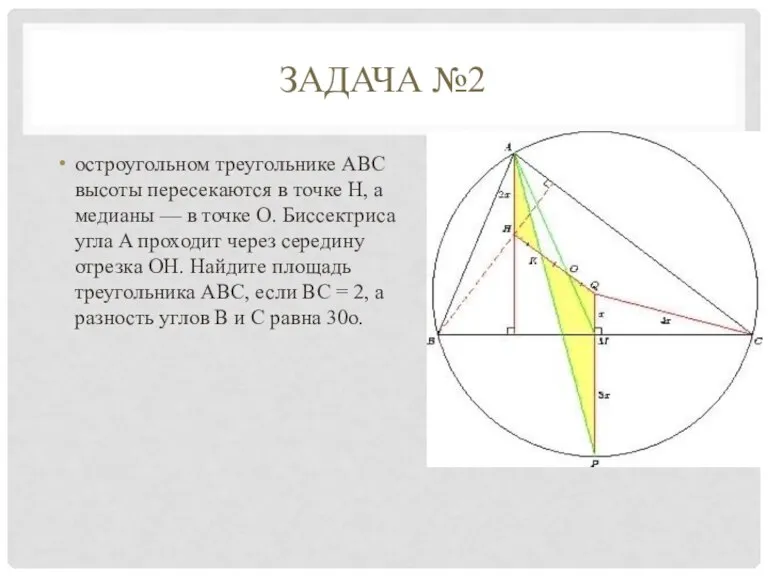
в точке O. Биссектриса угла A проходит через середину отрезка OH. Найдите площадь треугольника ABC, если BC = 2, а разность углов B и C равна 30o.










 Взаимно-обратные операции
Взаимно-обратные операции Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Презентация на тему Решение иррациональных неравенств (11 класс)
Презентация на тему Решение иррациональных неравенств (11 класс)  Диагностика и развитие мышления школьников на уроках математики
Диагностика и развитие мышления школьников на уроках математики Площадь трапеции. 8класс
Площадь трапеции. 8класс Функция
Функция Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Матрицы. Действия над матрицами
Матрицы. Действия над матрицами Математические методы в психологии. Генеральная совокупность и выборка
Математические методы в психологии. Генеральная совокупность и выборка Преобразование иррациональных выражений
Преобразование иррациональных выражений Презентация на тему Конус
Презентация на тему Конус  Сказ о дележе наследства (задача)
Сказ о дележе наследства (задача) Исследование функций и построение графиков
Исследование функций и построение графиков Аппроксимирующий полином Ньютона
Аппроксимирующий полином Ньютона Параллельный перенос
Параллельный перенос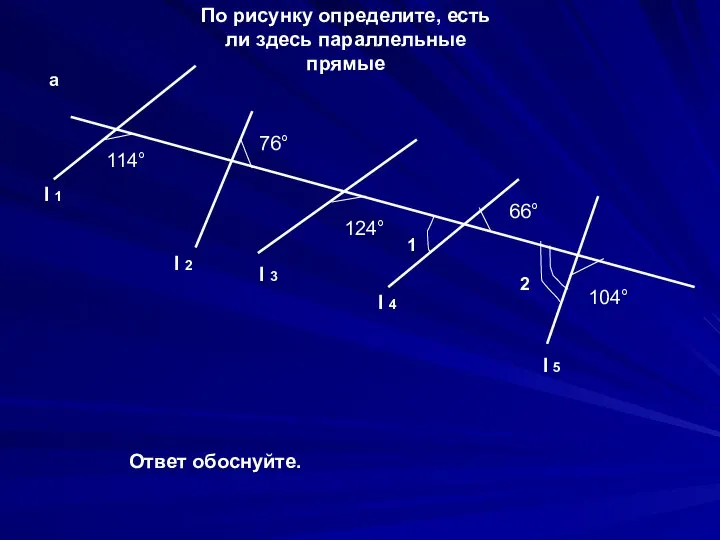 Параллельные прямые
Параллельные прямые Практические задания на применение формул сокращённого умножения
Практические задания на применение формул сокращённого умножения Таблица сложения в пределах 20
Таблица сложения в пределах 20 Готовимся к Всероссийским проверочным работам по математике
Готовимся к Всероссийским проверочным работам по математике Неравенство треугольника
Неравенство треугольника Решение показательных уравнений. Корень уравнения
Решение показательных уравнений. Корень уравнения Внеурочная деятельность по математике, 3 класс
Внеурочная деятельность по математике, 3 класс Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Таблица умножение на двух значное число
Таблица умножение на двух значное число Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Физический и геометрический смысл производной. Понятие дифференциал функции
Физический и геометрический смысл производной. Понятие дифференциал функции