Содержание
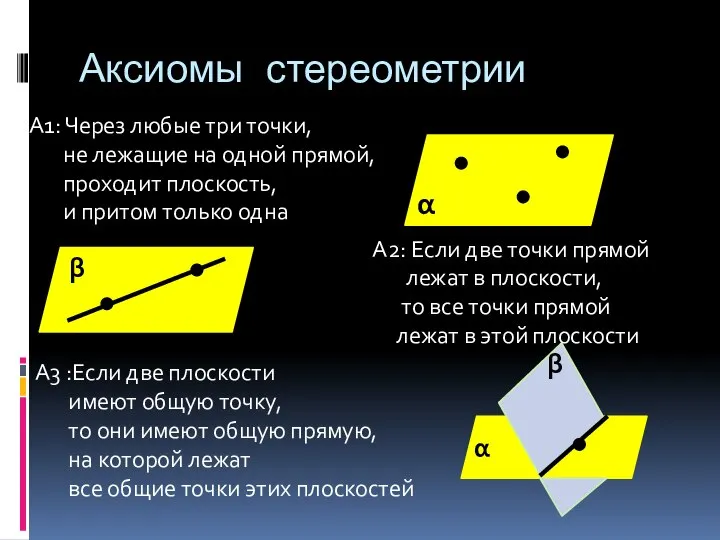
- 2. Аксиомы стереометрии А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом
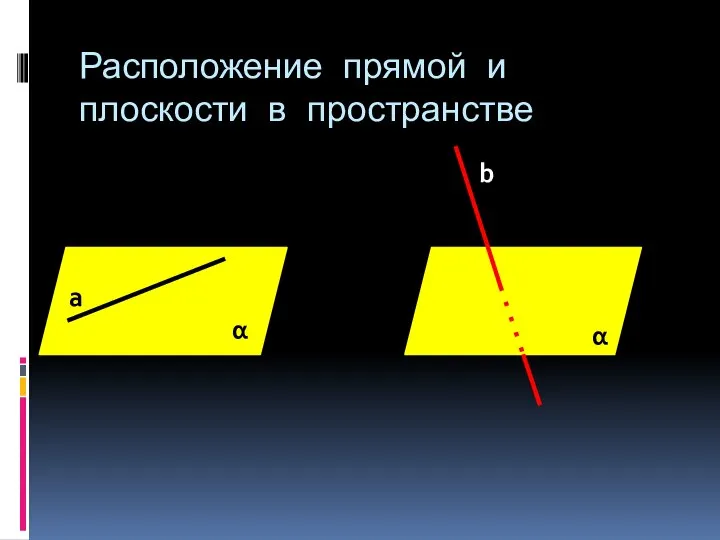
- 3. Расположение прямой и плоскости в пространстве α α а b
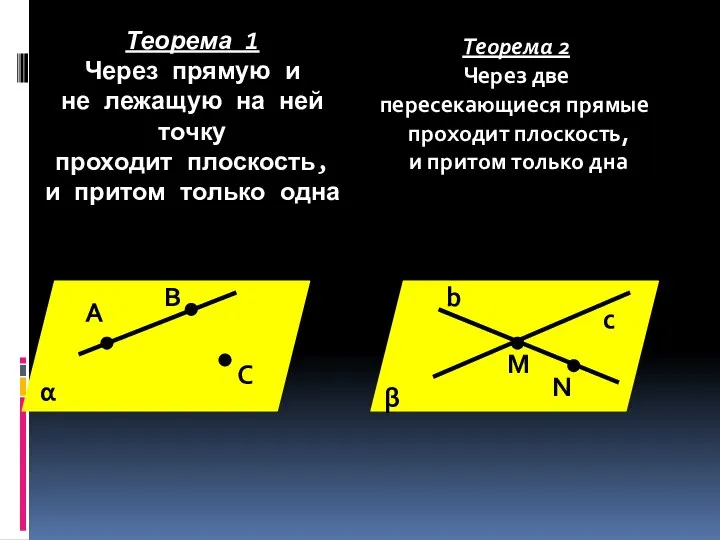
- 4. Теорема 1 Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна
- 5. Параллельность прямых и плоскостей Определение: две прямые в пространстве называются параллельными, если они лежат в одной
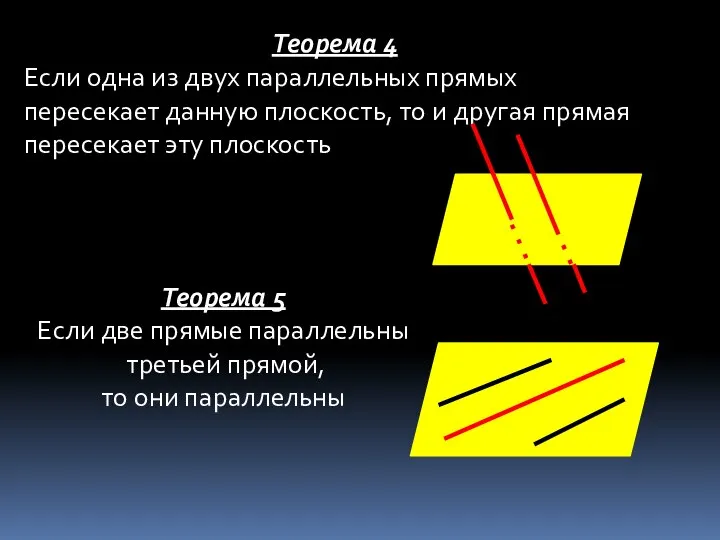
- 6. Теорема 4 Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает
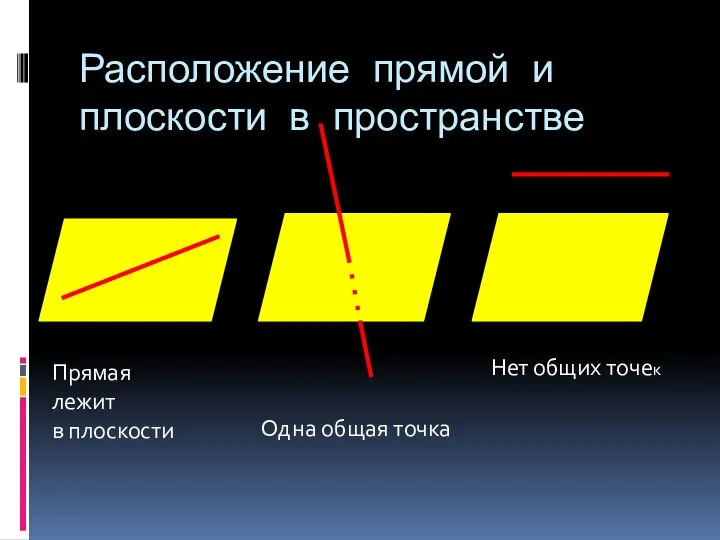
- 7. Расположение прямой и плоскости в пространстве Прямая лежит в плоскости Одна общая точка Нет общих точек
- 8. Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек Теорема 6 Если прямая,
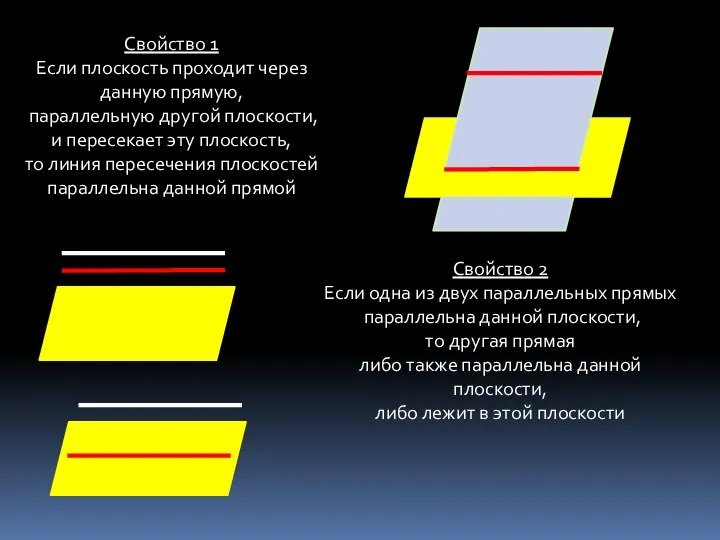
- 9. Свойство 1 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то
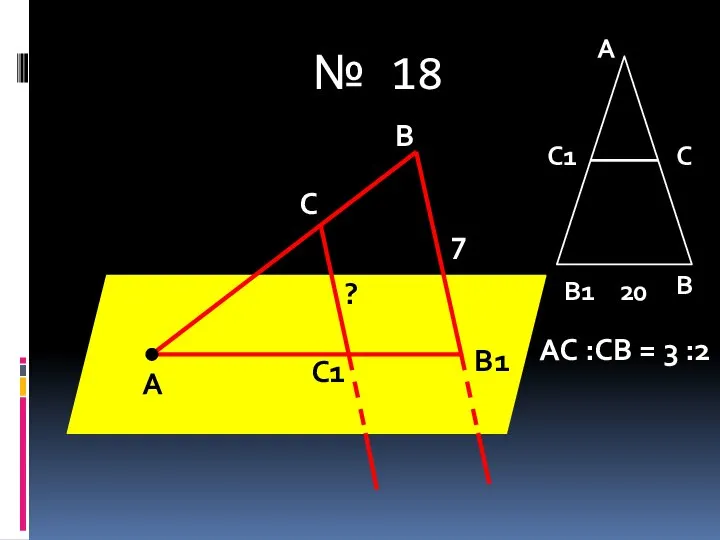
- 10. № 18 А В С С1 В1 7 ? А А В С В1 С1 20
- 12. Скачать презентацию


 Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Презентация на тему Площади и объемы
Презентация на тему Площади и объемы  Симметрия в искусстве
Симметрия в искусстве Векторы. Свойства равных векторов
Векторы. Свойства равных векторов Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач
Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим
Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим Примеры арифметических операций
Примеры арифметических операций Интегривование тригонометрических функций
Интегривование тригонометрических функций Шар. Сфера
Шар. Сфера Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Вписанный угол
Вписанный угол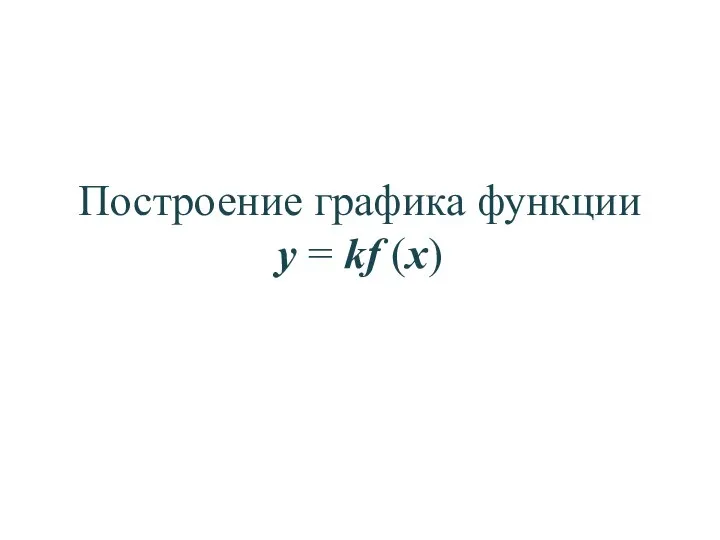 График функции y = kf (x)
График функции y = kf (x) Презентация на тему Знаки больше, меньше, равно (1 класс)
Презентация на тему Знаки больше, меньше, равно (1 класс)  Задание на треугольники
Задание на треугольники Сложение вида
Сложение вида Деление дробей
Деление дробей Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл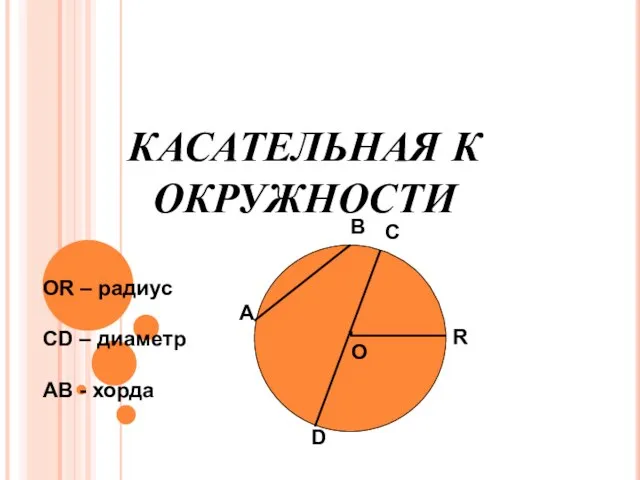 08.09
08.09 Справочный материал. 9 класс
Справочный материал. 9 класс Решение тестовых задач. Готовимся к ЕГЭ
Решение тестовых задач. Готовимся к ЕГЭ Преобразование тригонометрического выражения
Преобразование тригонометрического выражения Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Синус, косинус, тангенс
Синус, косинус, тангенс Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Графики кусочных функций
Графики кусочных функций Решение задач
Решение задач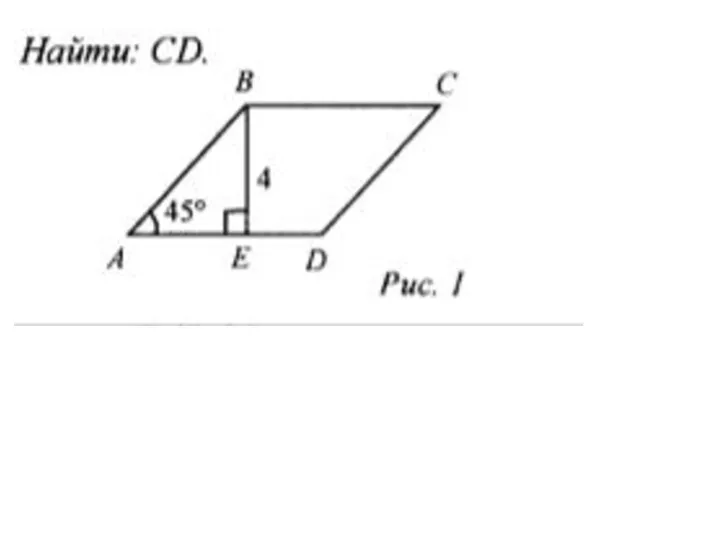 Вычисление площадей
Вычисление площадей Единицы, десятки
Единицы, десятки