Содержание
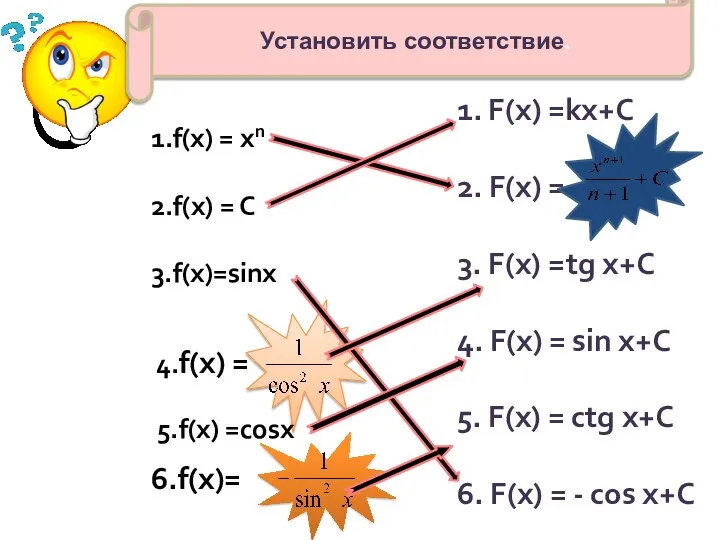
- 2. 1.f(x) = хn 2.f(x) = C 3.f(x)=sinx 4.f(x) = 6.f(x)= 1. F(x) =kх+С 2. F(x) =
- 3. Найти первообразные для функций: F(x) = 5 х² + C F(x) = х³ + C F(x)
- 4. Задание Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.
- 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b) называют совокупность первообразных функции.
- 6. Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции .
- 7. Лейбниц Готфрид Вильгельм (1646-1716) Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы
- 8. В развитии интегрального исчисления приняли участие русские математики: М.В. Остроградский (1801 – 1862) В.Я. Буняковский (1804
- 9. Примеры
- 11. Свойства интеграла
- 12. Свойства интеграла
- 13. Верно ли что: а) в) б) г) г)
- 15. Пример №2
- 16. Пример №3 (формула 4 таблицы интегралов)
- 17. Пример №4 (формула 3)
- 18. Пример №5
- 19. Пример №1 Интеграл суммы выражений равен сумме интегралов этих выражений Постоянный множитель можно вынести за знак
- 20. Пример №2 Записать решение: Проверить решение ?
- 21. Пример №3 Записать решение: Проверить решение ?
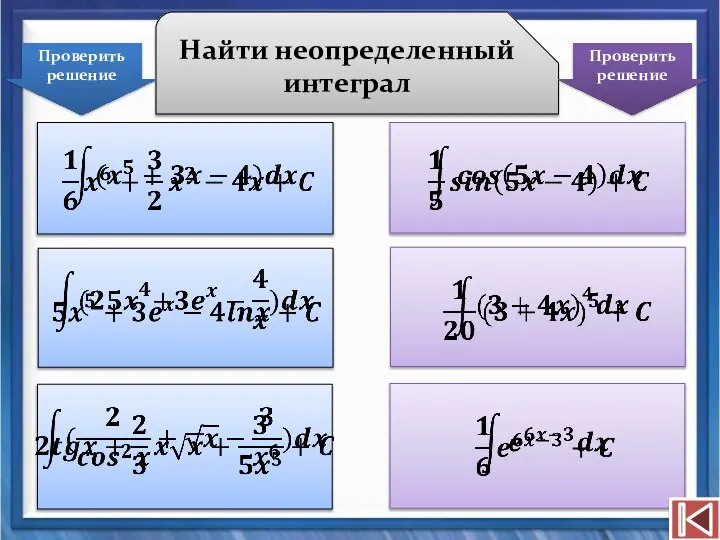
- 22. Найти неопределенный интеграл Проверить решение Проверить решение
- 23. Следует отметить, что для функции вида f(kx+b) можно применять упрощенную формулу
- 26. Скачать презентацию












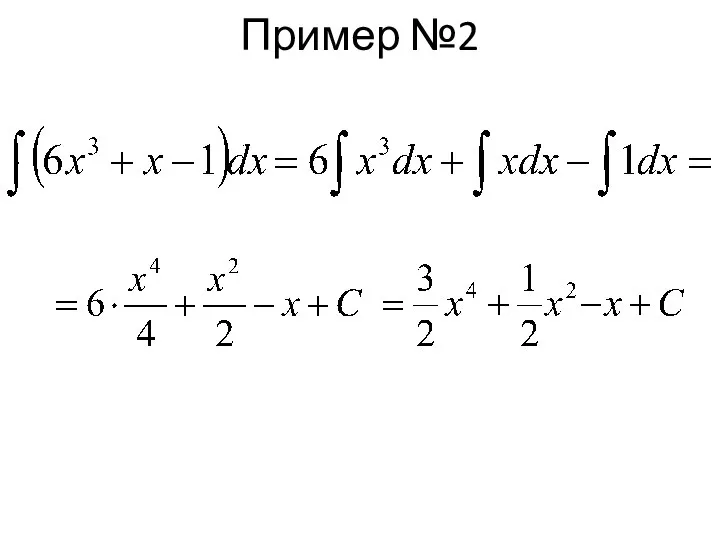







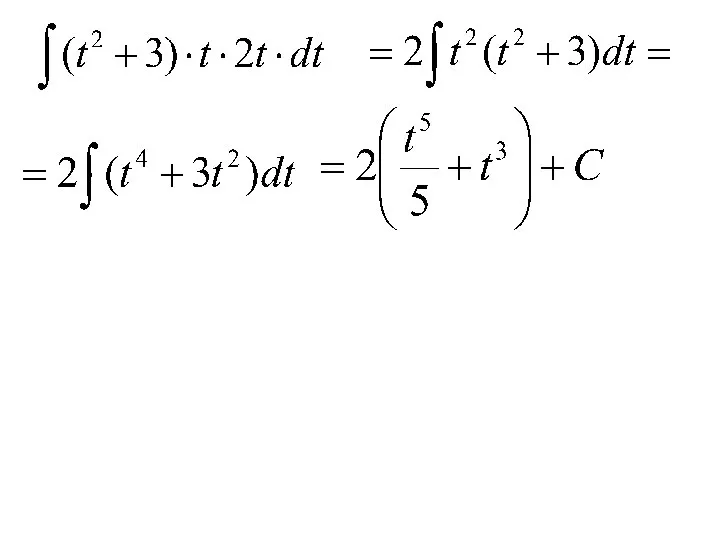
 Приемы вычислений для случаев вида 26+7. 2 класс
Приемы вычислений для случаев вида 26+7. 2 класс Презентация на тему Цилиндр (11 класс)
Презентация на тему Цилиндр (11 класс)  Комбинация фигур
Комбинация фигур От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Математическая викторина. Блок 1 и 2
Математическая викторина. Блок 1 и 2 Презентация
Презентация Презентация на тему Анализ геометрической формы предмета
Презентация на тему Анализ геометрической формы предмета  Числа, кратные 3
Числа, кратные 3 Преобразование графиков 9-10 классы
Преобразование графиков 9-10 классы Подготовка к изучению чисел
Подготовка к изучению чисел Иррациональные неравенства
Иррациональные неравенства Упрощение выражений (5 лкасс)
Упрощение выражений (5 лкасс) Построение сечений
Построение сечений Конус. Основные элементы конуса
Конус. Основные элементы конуса Понятие числовой окружности. Радианное измерение углов
Понятие числовой окружности. Радианное измерение углов Б. Кавальери и его метод неделимых
Б. Кавальери и его метод неделимых Квадрат. Прямоугольник
Квадрат. Прямоугольник Математический марафон
Математический марафон Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ  Состав чисел в приделах 10. Решение задач
Состав чисел в приделах 10. Решение задач Математка в жизни
Математка в жизни Lecture 7
Lecture 7 Семейство четырехугольников
Семейство четырехугольников Решение линейных уравнений
Решение линейных уравнений Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Геометрическая оптика. 11 класс. ЕГЭ
Геометрическая оптика. 11 класс. ЕГЭ Решение задач на проценты
Решение задач на проценты Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия