Содержание
- 2. Группой учёных под руководством Баутина С.П. в ряде работ предлагается математическое описание восходяцих закрученных потоков, учитывающее
- 3. ПСУНС в цилиндрических координатах уравнение неразрывности окружная скорость радиальная скорость вертикальная скорость уравнение энергии
- 4. Регулярная сетка в цилиндрических координатах задаётся шагом по длине радиуса hr, высоте выбранного объёма hz и
- 5. Конечно-разностная схема Замена частных производных по координатам:
- 6. Уравнение неразрывности
- 7. Радиальная скорость
- 8. Окружная скорость
- 9. Вертикальная скорость
- 10. Уравнение энергии
- 11. Выводы Решение полученной системы алгебраических уравнений описывает поведение воздушных масс в поле силы тяжести с учётом
- 12. Список использованной литературы Разрушительные атмосферные вихри и вращение Земли вокруг своей оси: монография / С.П.Баутин, С.Л.Дерябин,
- 13. Спасибо за внимание!
- 15. Сила Кориолиса и ее проявления Рисунок 3 – Декартова система координат, вращающаяся вместе с Землёй Будем
- 16. Полная система уравнений Навье-Стокса Запишем полную систему уравнений Навье-Стокса в размерных переменных, учитывающею законы сохранения, вязкость
- 18. Скачать презентацию















 Тригонометрические функции
Тригонометрические функции Презентация на тему Операции. Обратные операции
Презентация на тему Операции. Обратные операции  Системы уравнений
Системы уравнений Цилиндр
Цилиндр Больше, меньше, столько же
Больше, меньше, столько же Многогранник
Многогранник Куб. Параллелепипед. Тест
Куб. Параллелепипед. Тест Теорема Пифагора
Теорема Пифагора Параллельность плоскостей
Параллельность плоскостей Алгоритмы растеризации
Алгоритмы растеризации Сложение и вычитание векторов
Сложение и вычитание векторов Интерактивный плакат Треугольник
Интерактивный плакат Треугольник Задача о спортсменах
Задача о спортсменах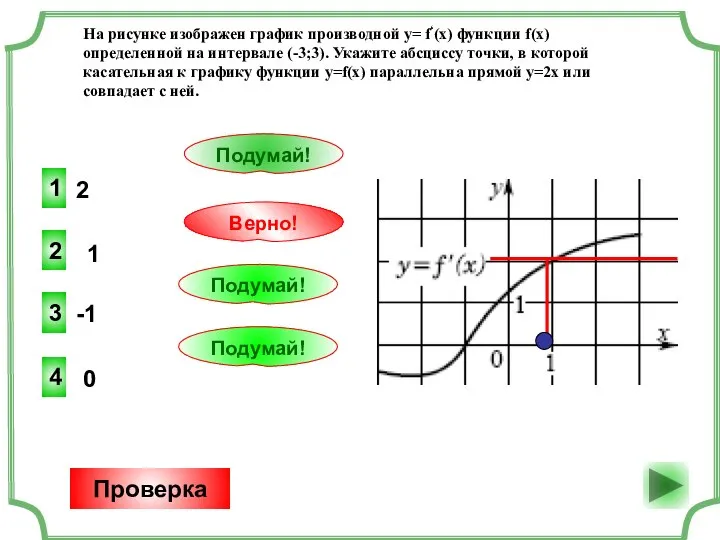 Решение задач
Решение задач Планиметрия. Треугольники и четырехугольники. Готовимся к ГИА
Планиметрия. Треугольники и четырехугольники. Готовимся к ГИА Объем конуса, цилиндра
Объем конуса, цилиндра Міра. Однозначні, багатозначні міри
Міра. Однозначні, багатозначні міри Дискриминантный анализ Фишера с kernel trick
Дискриминантный анализ Фишера с kernel trick Действия с функциями (9 задание ЕГЭ)
Действия с функциями (9 задание ЕГЭ) Система упражнений по изучению свойств линейной функции
Система упражнений по изучению свойств линейной функции Прямоугольный параллелепипед
Прямоугольный параллелепипед Корень уравнения
Корень уравнения Предметы геометрической формы. Логические задания
Предметы геометрической формы. Логические задания С математикой в космос
С математикой в космос Презентация на тему Умножение многочлена на многочлен
Презентация на тему Умножение многочлена на многочлен  Системы уравнений
Системы уравнений Построение сечений в тетраэдре
Построение сечений в тетраэдре Функции и их свойства. Область определения и область значений функции
Функции и их свойства. Область определения и область значений функции