помощью двух инструментов: циркуля и линейки без масштабных делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16


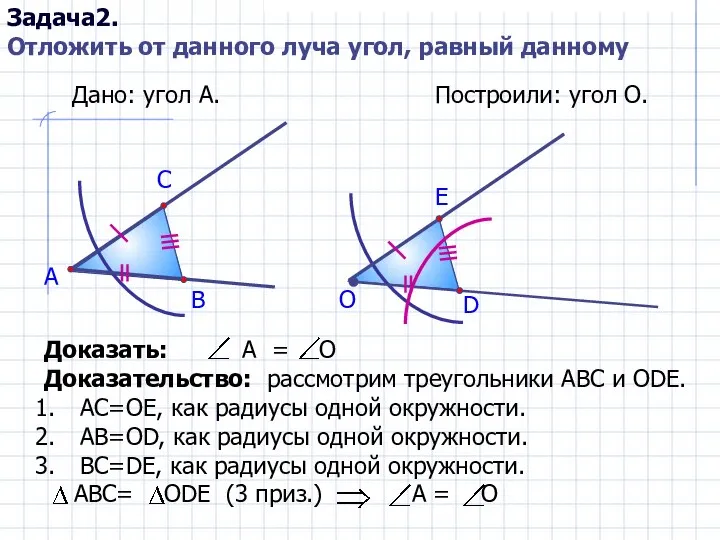
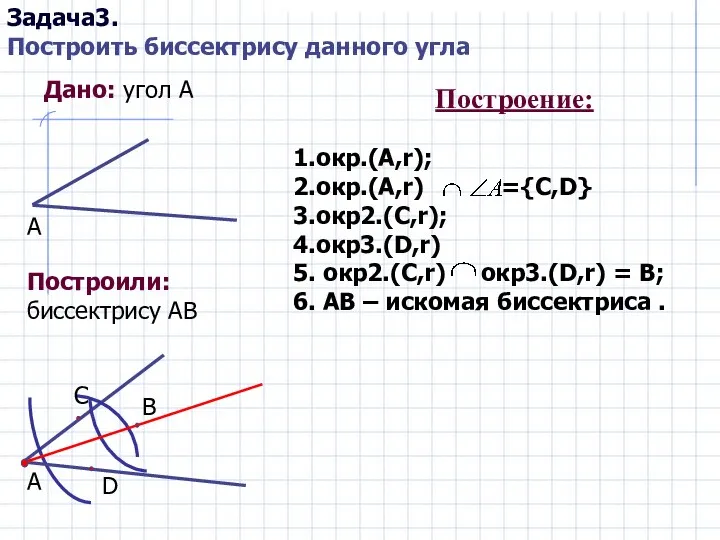
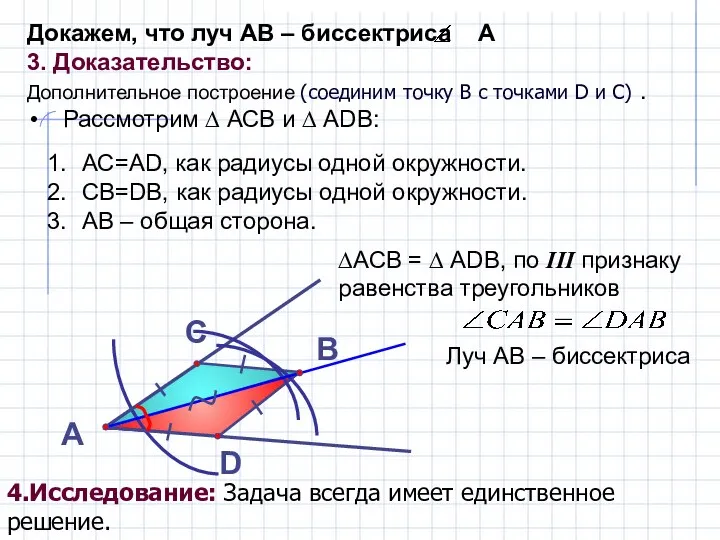
 Массивы. Двумерные массивы. Спиралевидный и змеевидный обходы
Массивы. Двумерные массивы. Спиралевидный и змеевидный обходы Статистический анализ состава и использования фонда. Темпы роста фонда, числа читателей и книговыдачи
Статистический анализ состава и использования фонда. Темпы роста фонда, числа читателей и книговыдачи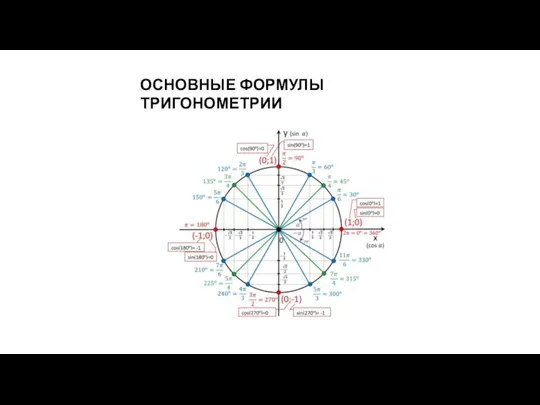 Основные формулы тригонометрии
Основные формулы тригонометрии Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов
Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов  Множества и операции над ними
Множества и операции над ними Презентация на тему Магия чисел 9 класс
Презентация на тему Магия чисел 9 класс  Решение уравнений и построение точек по их координатам. 6 класс
Решение уравнений и построение точек по их координатам. 6 класс Решение задач. Тест
Решение задач. Тест Правила сложения сил и условия равновесия твердых тел
Правила сложения сил и условия равновесия твердых тел Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Множества. 8 класс
Множества. 8 класс Розв'язання задач
Розв'язання задач Площадь параллелограмма
Площадь параллелограмма Занимательные задачи (4 класс)
Занимательные задачи (4 класс) Отрезок, луч, прямая. Графический диктант 1. 5 класс
Отрезок, луч, прямая. Графический диктант 1. 5 класс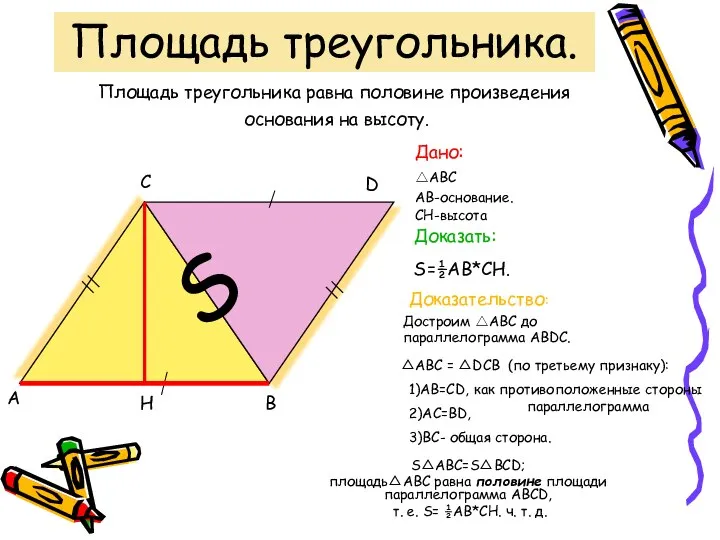 Площадь треугольника
Площадь треугольника Понятие доли
Понятие доли Углы с сонаправленными сторонами
Углы с сонаправленными сторонами Задачи на построение сечений
Задачи на построение сечений Основные формулы
Основные формулы Правильная треугольная усечённая пирамида
Правильная треугольная усечённая пирамида Понятие о проценте
Понятие о проценте Кристаллография. Вывод 32 точечных групп симметрии в обозначениях по шенфлису. Трансляционные элементы симметрии
Кристаллография. Вывод 32 точечных групп симметрии в обозначениях по шенфлису. Трансляционные элементы симметрии Обыкновенные дроби. Основное свойство дроби. 5 класс
Обыкновенные дроби. Основное свойство дроби. 5 класс Дробные рациональные уравнения
Дробные рациональные уравнения Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия Презентация на тему Движение. Виды движения
Презентация на тему Движение. Виды движения  Презентация на тему Вектор
Презентация на тему Вектор