Содержание
- 2. Использование свойств производной для исследования функций Задание 6 использование свойств производной при анализе функций, геометрический смысл
- 3. Физический смысл производной Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета
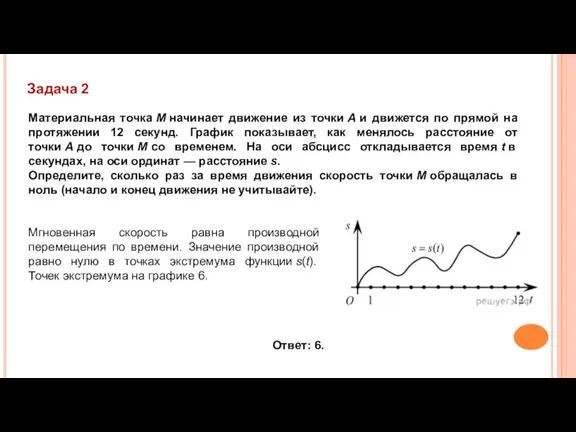
- 4. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд.
- 5. Геометрический смысл производной Монотонность функции. Промежутки возрастания и убывания Точки экстремума функции Понятие о производной функции,
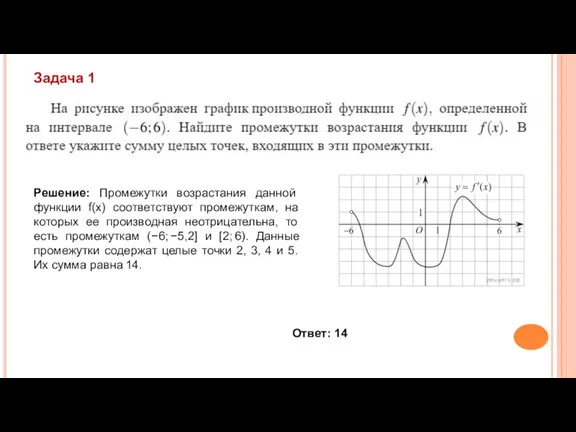
- 7. Решение: Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых ее производная неотрицательна, то есть промежуткам
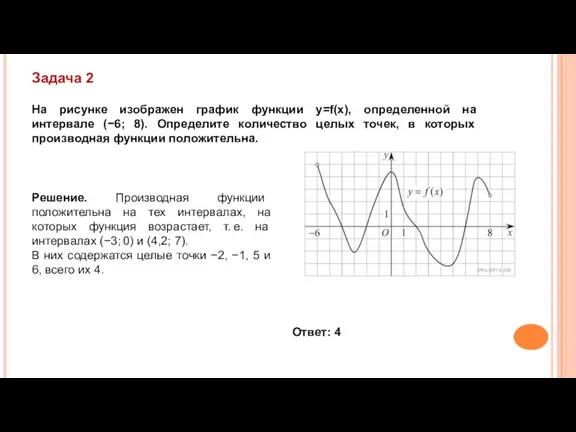
- 8. На рисунке изображен график функции y=f(x), определенной на интервале (−6; 8). Определите количество целых точек, в
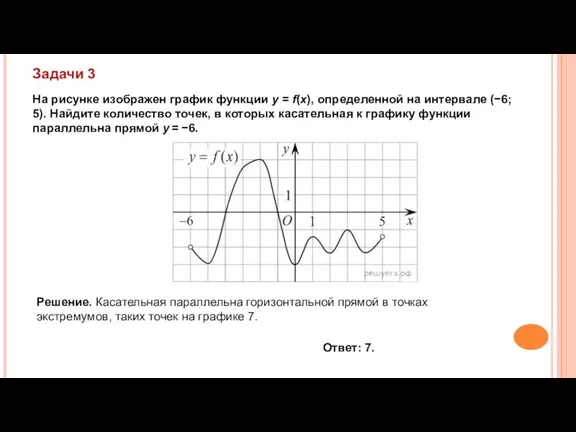
- 9. На рисунке изображен график функции y = f(x), определенной на интервале (−6; 5). Найдите количество точек,
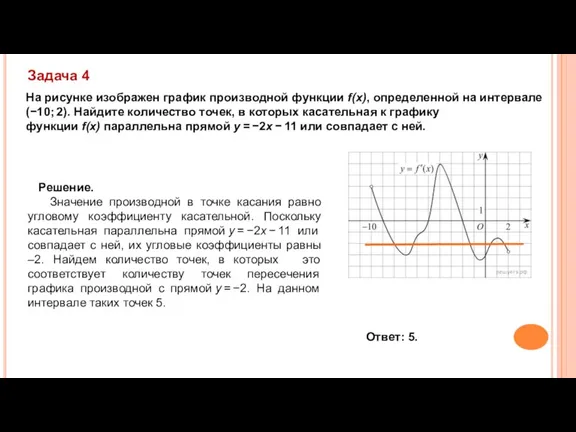
- 10. На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в
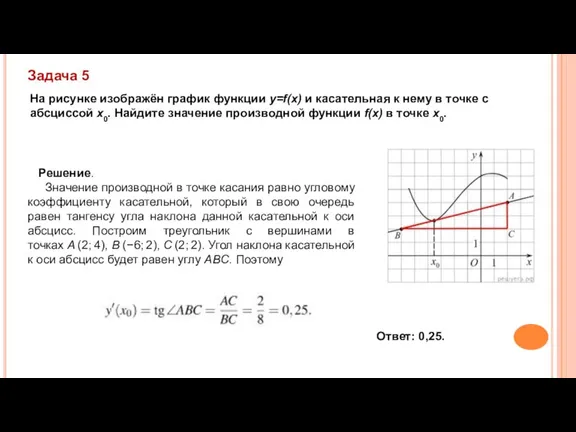
- 11. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите
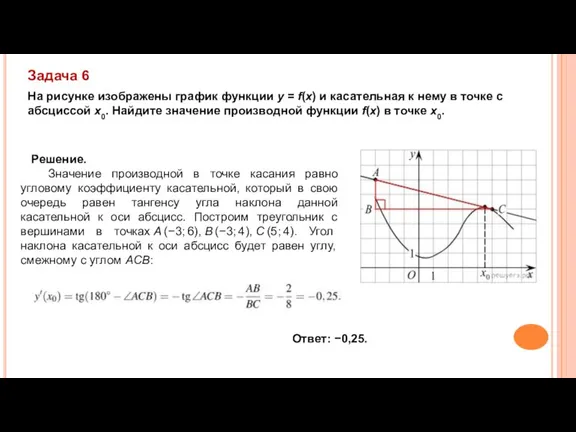
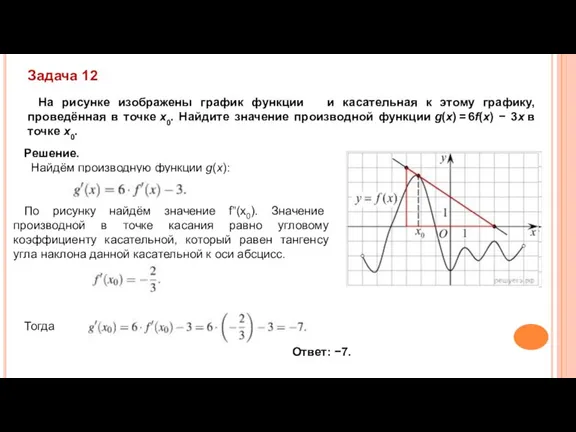
- 12. Задача 6 На рисунке изображены график функции y = f(x) и касательная к нему в точке
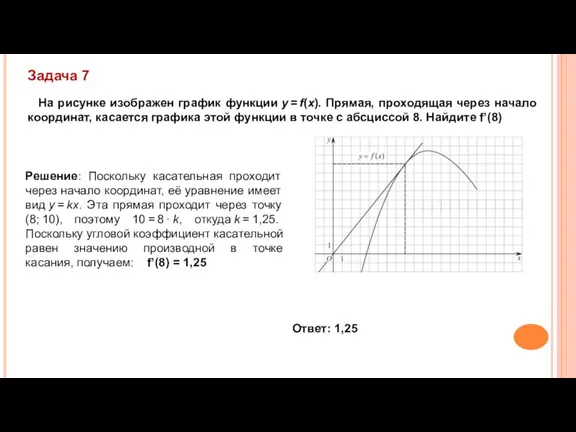
- 13. Задача 7 На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается
- 14. Задача 8 Ответ: 0,5.
- 15. Задача 10 Проверка подстановкой показывает, что первый корень не удовлетворяет, а второй удовлетворяет уравнению (*). Поэтому
- 16. Задача 11
- 17. На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение
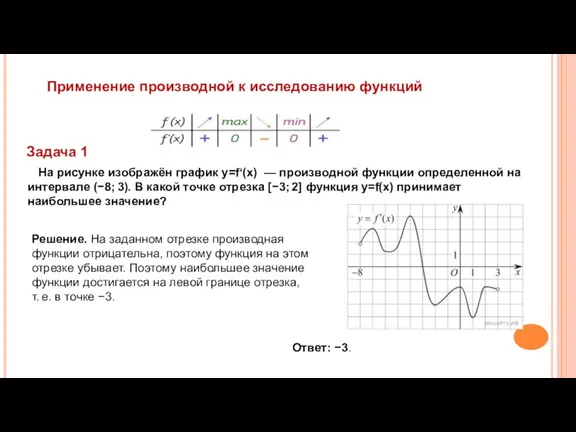
- 18. Применение производной к исследованию функций На рисунке изображён график y=f‘(x) — производной функции определенной на интервале
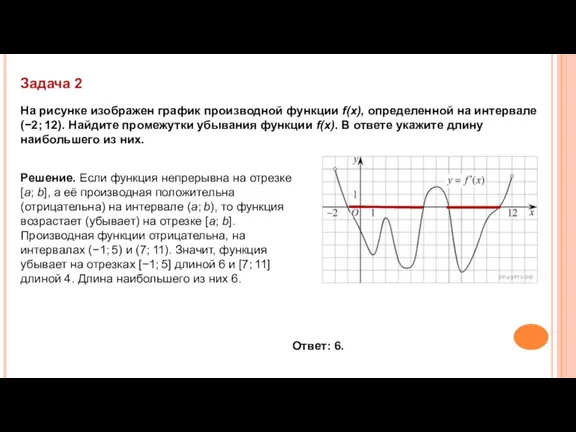
- 19. Задача 2 На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки
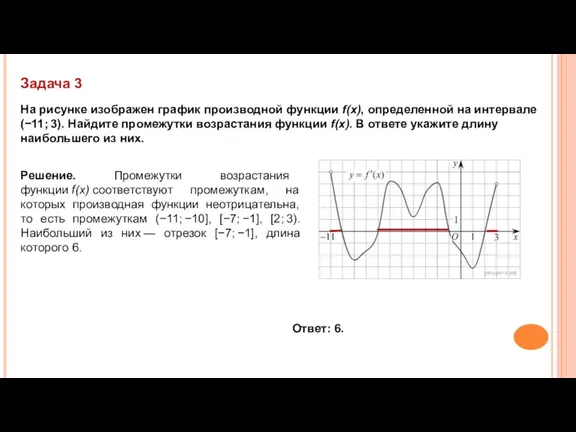
- 20. Задача 3 На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки
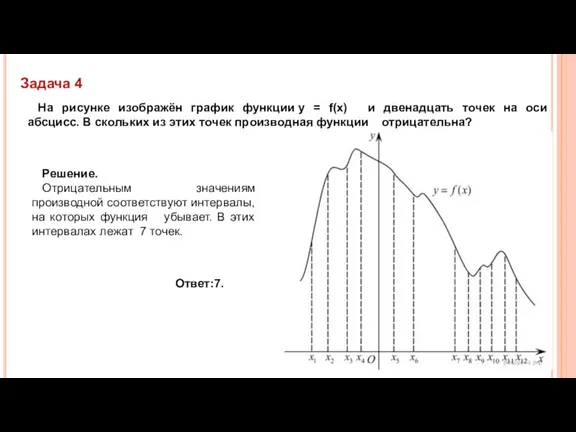
- 21. Задача 4 На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс.
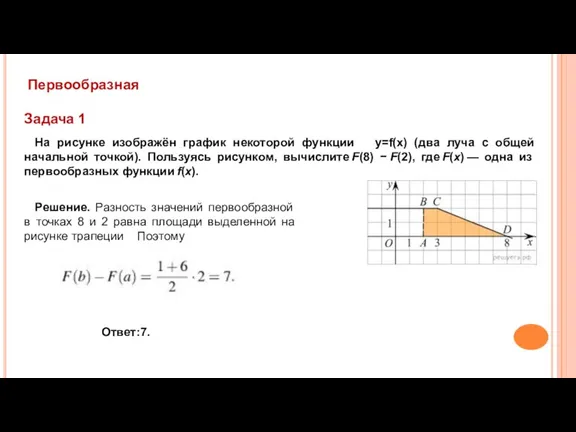
- 22. Первообразная Задача 1 На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой).
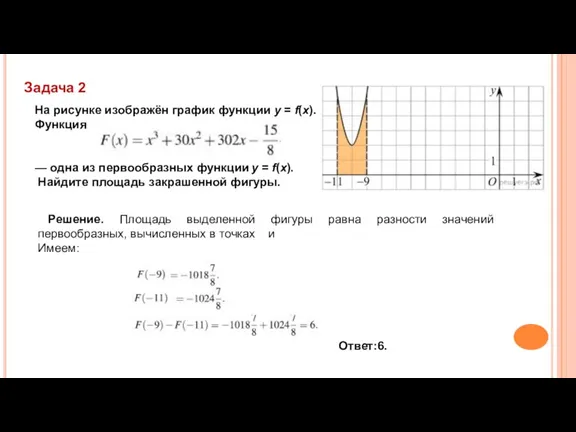
- 23. Задача 2 На рисунке изображён график функции y = f(x). Функция — одна из первообразных функции
- 24. Задание 11 нахождение точек максимума и минимума функции нахождение наибольшего и наименьшего значения функции
- 25. Задача 1 Исследование степенных и иррациональных функций Найдите точку максимума функции Решение. Найдем производную заданной функции:
- 26. Задача 2 Найдите точку минимума функции Определим знаки производной функции и изобразим на рисунке поведение функции:
- 27. Задача 1 Исследование частных Найдите наименьшее значение функции на отрезке Решение. Найдем производную заданной функции: Найдем
- 28. Задача 1 Исследование произведений В точке x=7 заданная функция имеет максимум. Найдем наибольшее значение: y(7) =
- 29. Задача 1 Исследование показательных и логарифмических функций Ответ: −4,5.
- 30. Исследование тригонометрических функций Задача 1 Найдите наибольшее значение функции на отрезке Решение. Найдем производную заданной функции:
- 31. Задача 1 Исследование функций без помощи производной Найдите точку максимума функции Решение. Квадратный трехчлен с отрицательным
- 33. Скачать презентацию















 Решение заданий ЕГЭ уровня С2 (1 часть)
Решение заданий ЕГЭ уровня С2 (1 часть) Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Признаки делимости на 2, 5,10, 3, 6 и 9
Признаки делимости на 2, 5,10, 3, 6 и 9 Параллельные прямые в пространстве
Параллельные прямые в пространстве Неопределенный интеграл
Неопределенный интеграл Урок 53. Расстояние от точки до прямой
Урок 53. Расстояние от точки до прямой Степень с рациональным показателем
Степень с рациональным показателем Косинус угла
Косинус угла Производная сложной функции
Производная сложной функции Понятие вектора
Понятие вектора Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Задания на развитие логики
Задания на развитие логики 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций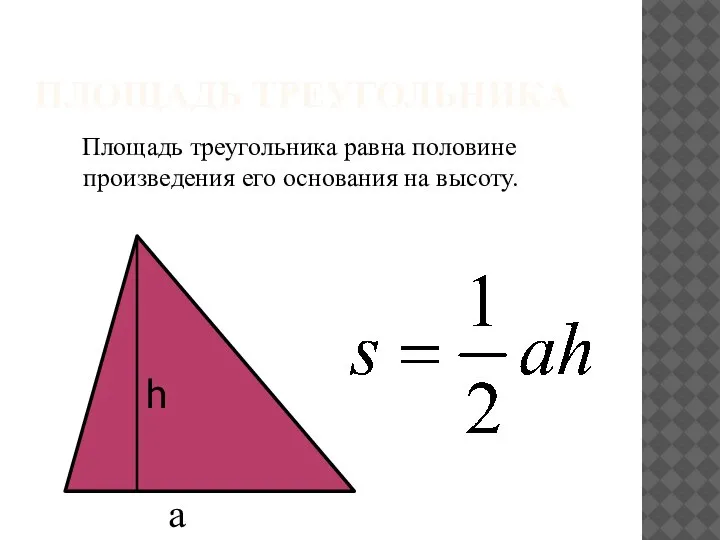 Площадь треугольника
Площадь треугольника Математика без границ. Конкурс
Математика без границ. Конкурс Сантиметр. Линейка
Сантиметр. Линейка Золотое сечение
Золотое сечение Информатика. Вероятность
Информатика. Вероятность Загадки и тайны треугольника
Загадки и тайны треугольника Сложение вида + 2, + 3
Сложение вида + 2, + 3 Презентация на тему Признаки равенства треугольников
Презентация на тему Признаки равенства треугольников  Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Умножение одночлена на многочлен
Умножение одночлена на многочлен Современная финансовая математика
Современная финансовая математика Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Плоскость и прямая в пространстве
Плоскость и прямая в пространстве