Содержание
- 2. СОДЕРЖАНИЕ Ортоцентр Точка пересечения медиан Точки, симметричные ортоцентру относительно сторон треугольника Точка Торричелли Прямая Симпсона Окружность
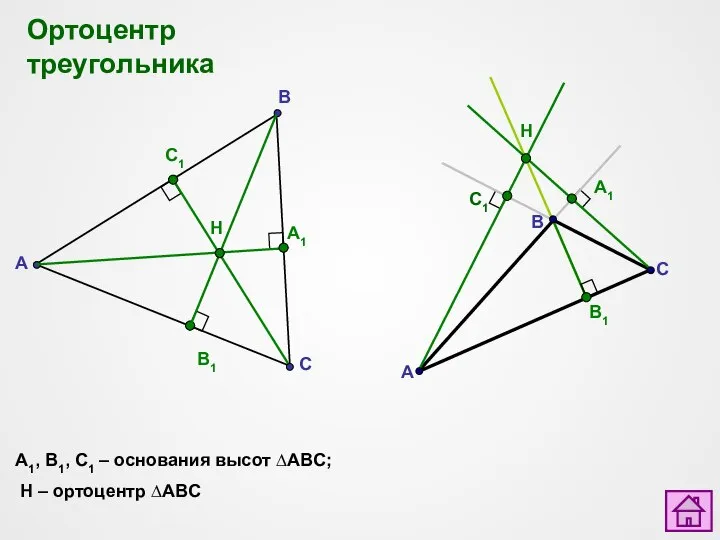
- 3. Ортоцентр треугольника A1, B1, C1 – основания высот ∆ABC; H – ортоцентр ∆ABC A C B
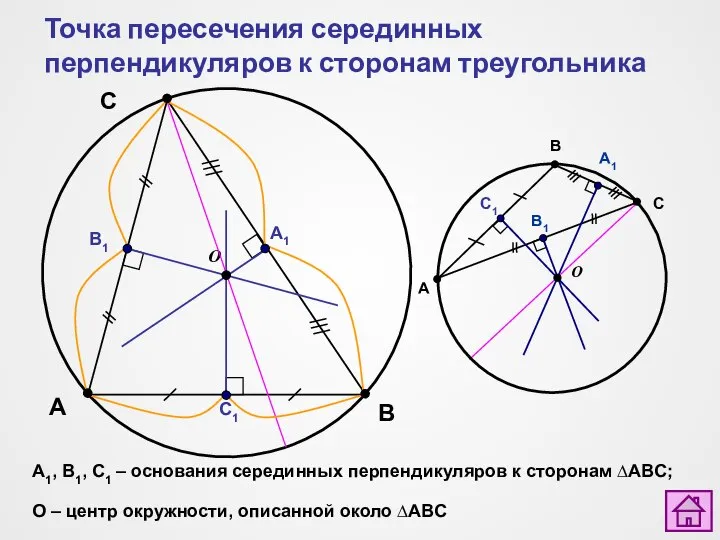
- 4. Точка пересечения серединных перпендикуляров к сторонам треугольника A B C О С1 В1 А1 A1, B1,
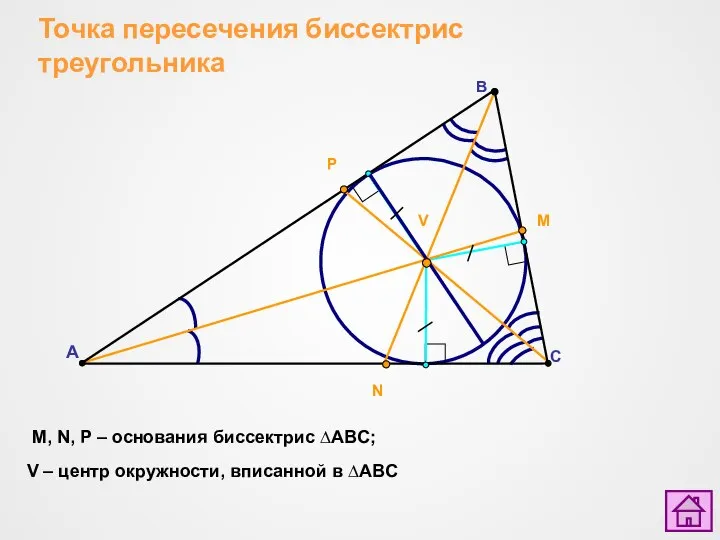
- 5. Точка пересечения биссектрис треугольника A C B V M N P M, N, P – основания
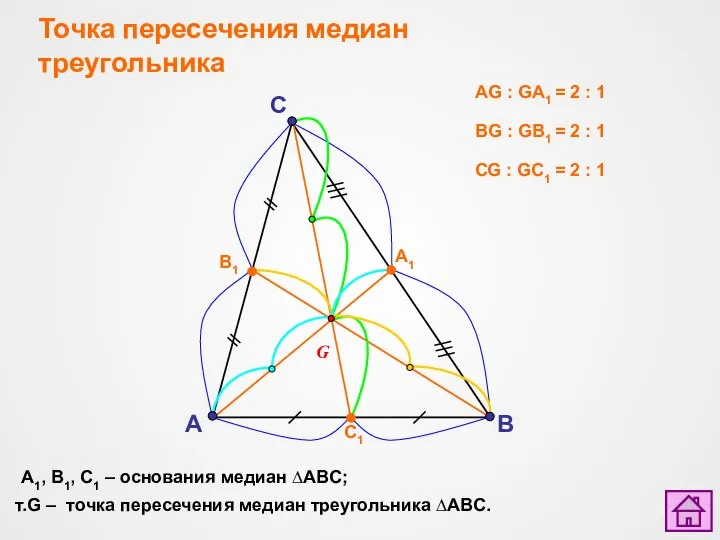
- 6. Точка пересечения медиан треугольника A B т.G – точка пересечения медиан треугольника ∆ABC. G С1 В1
- 7. A C B B1 H A1 C1 А2 A1, B1, C1 – основания высот; H –
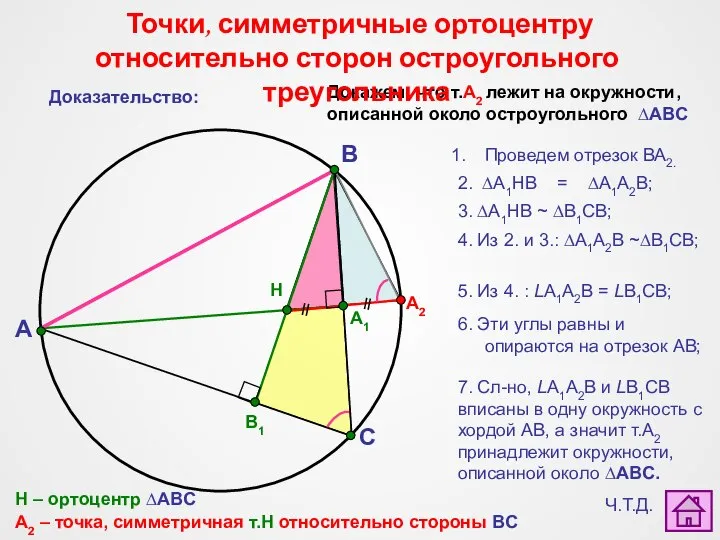
- 8. Докажем, что т.А2 лежит на окружности, описанной около остроугольного ∆ABC A C B H А2 H
- 9. A C B H A1 В2 B1 А2 НА1 = А1А2 C1 C2 НB1 = B1B2
- 10. A C B H A1 В2 B1 А2 НА1 = А1А2 C1 C2 НB1 = B1B2
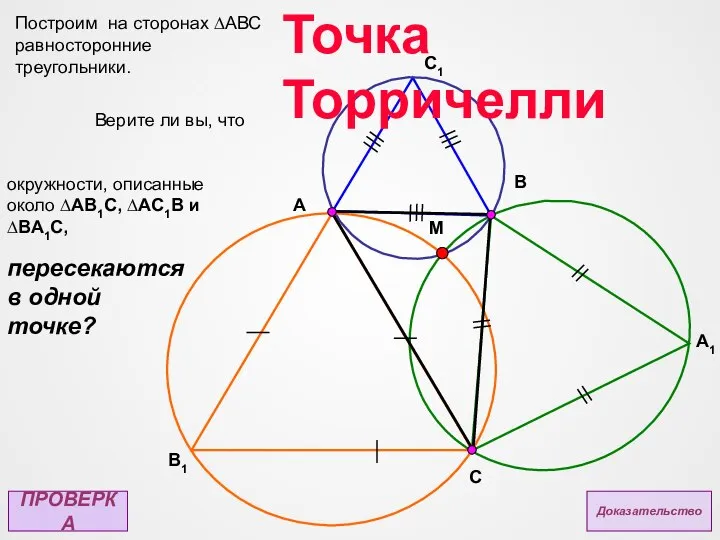
- 11. Верите ли вы, что окружности, описанные около ∆AB1C, ∆AC1В и ∆BА1C, ПРОВЕРКА Доказательство A1 A B1
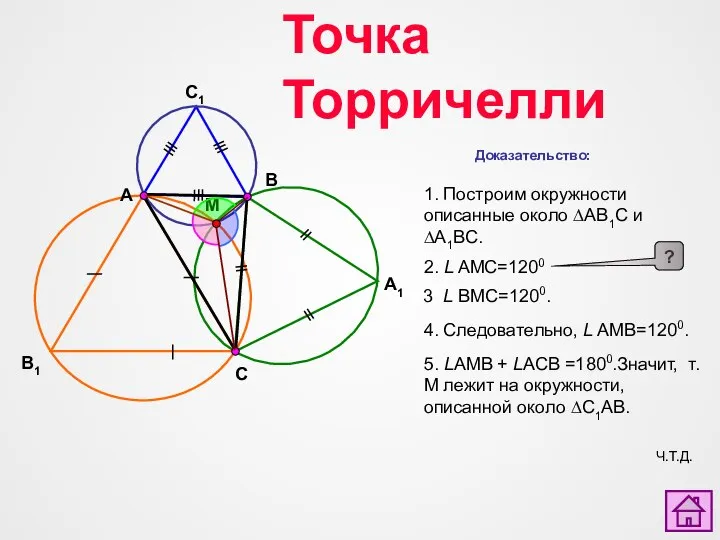
- 12. A1 A B1 C1 B C M Доказательство: 2. L AMC=1200 3 L BMC=1200. 4. Следовательно,
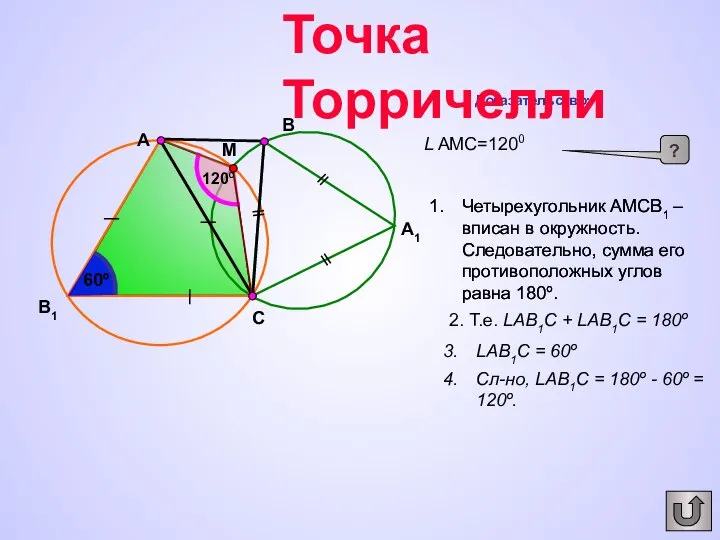
- 13. A1 A B1 B C M Доказательство: L AMC=1200 ? Четырехугольник АМСВ1 – вписан в окружность.
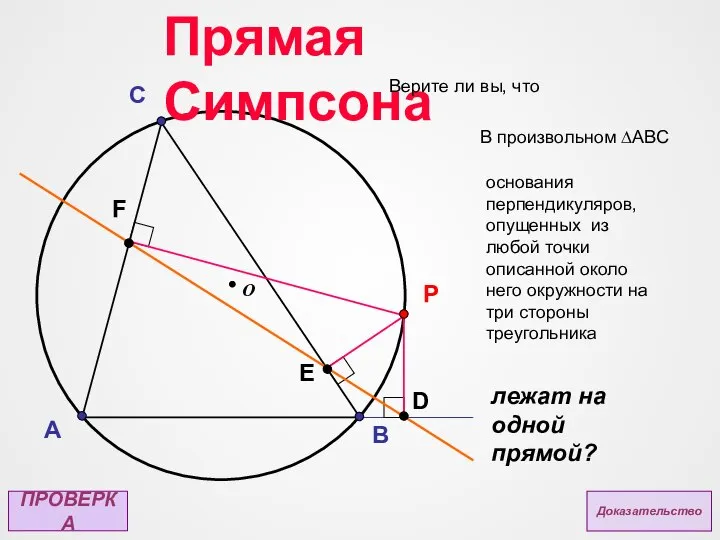
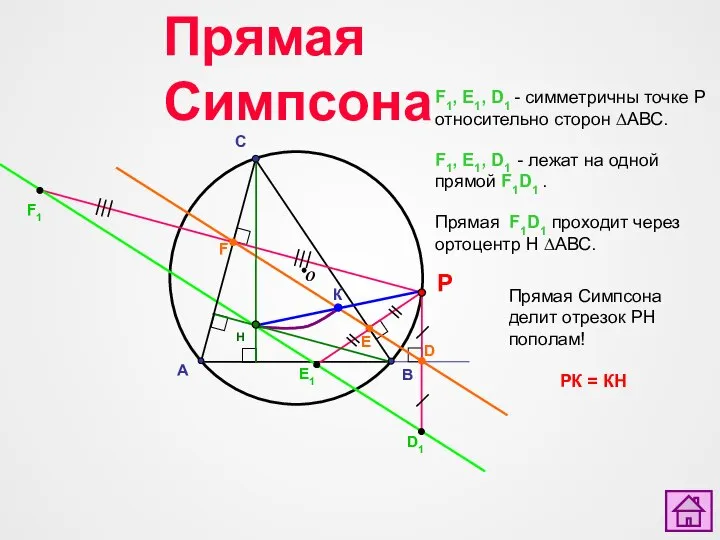
- 14. A B C О P F E D Прямая Симпсона Верите ли вы, что Доказательство ПРОВЕРКА
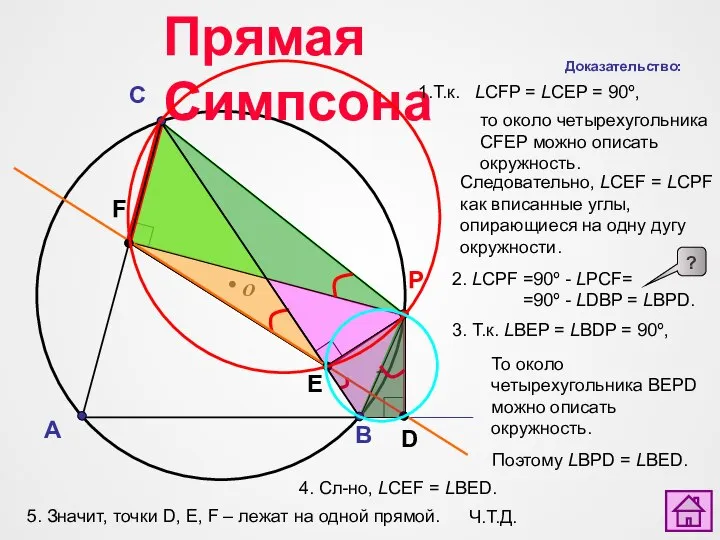
- 15. A B C О P F E D Прямая Симпсона Доказательство: 1.Т.к. LCFP = LCEP =
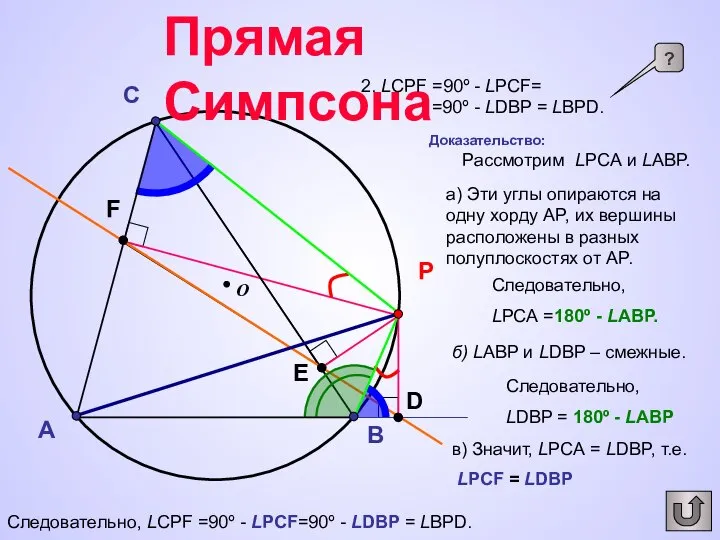
- 16. A B C О P F E D Прямая Симпсона Доказательство: Рассмотрим LPCА и LАBP. а)
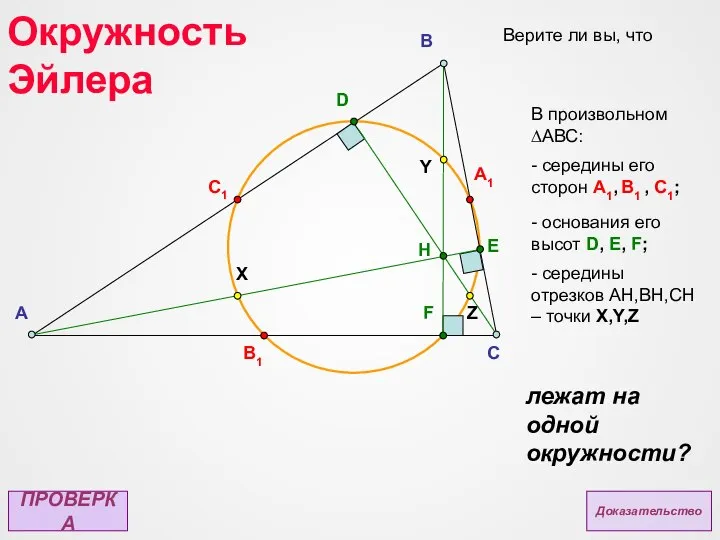
- 17. A C B E D F B1 A1 C1 X Y Z Верите ли вы, что
- 18. A C B B1 A1 C1 X Y Z E D F H Доказательство: 1. Т.к.
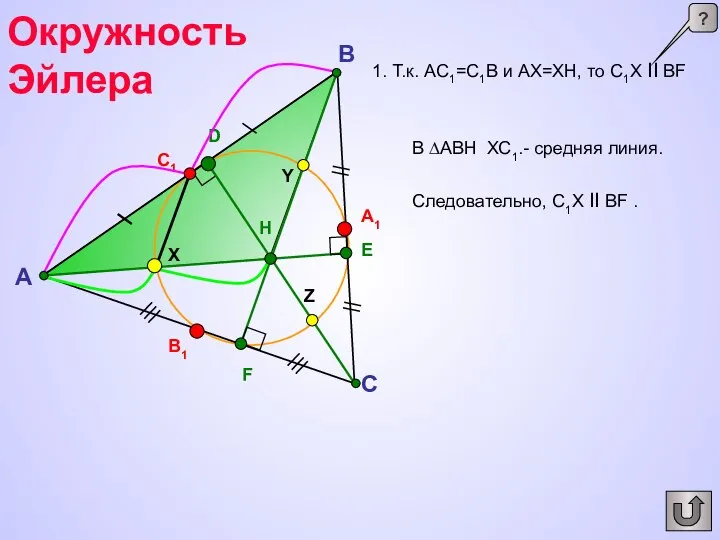
- 19. A C B B1 A1 C1 X Y Z E D F H 1. Т.к. АС1=С1В
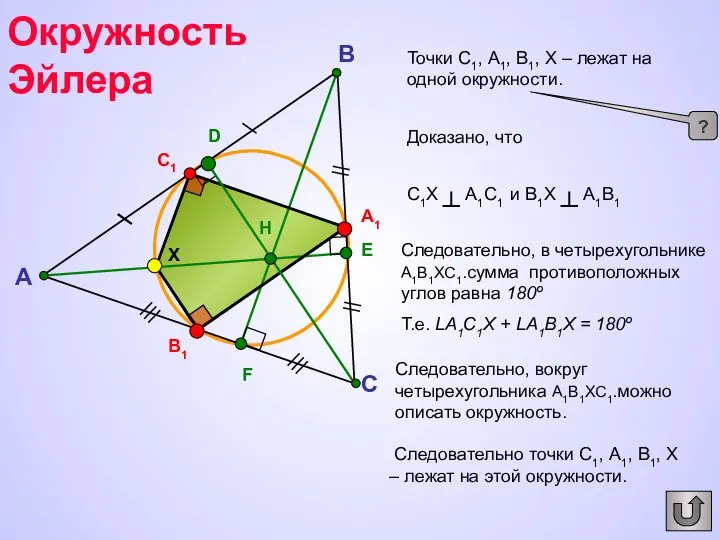
- 20. A C B B1 A1 C1 X E D F H Точки С1, А1, В1, Х
- 21. A C B E D F B1 A1 C1 X Y Z Верите ли вы, что
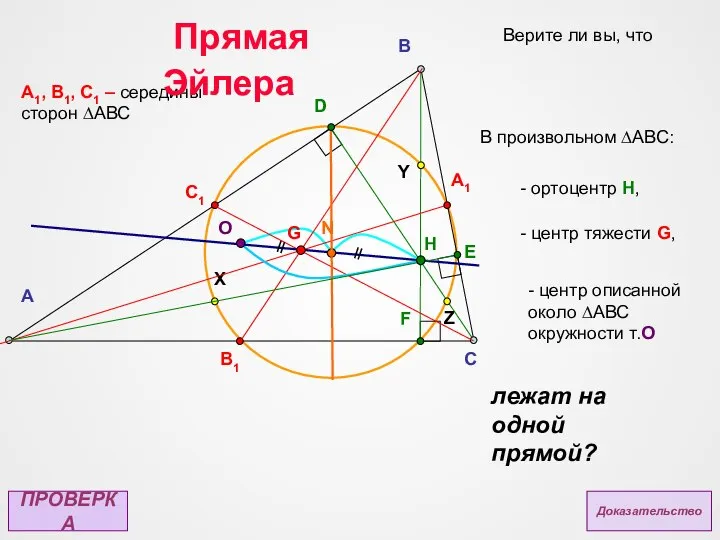
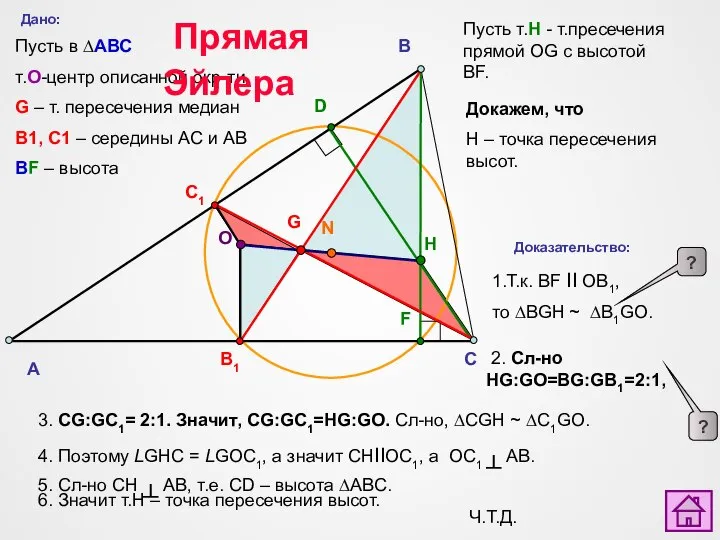
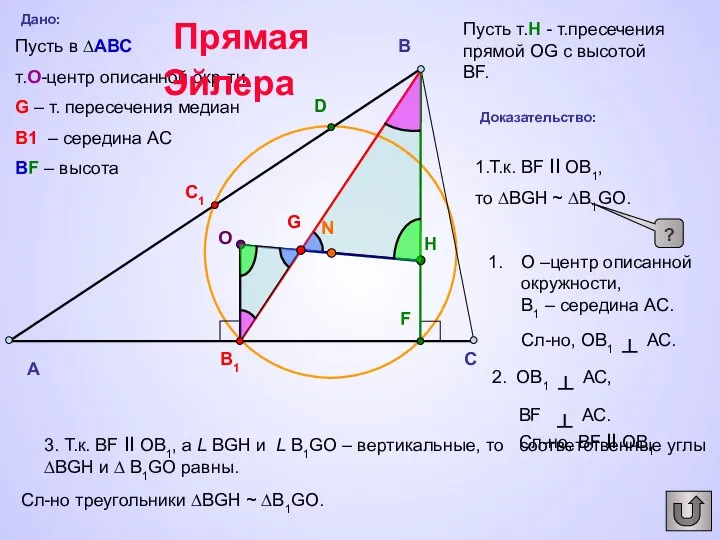
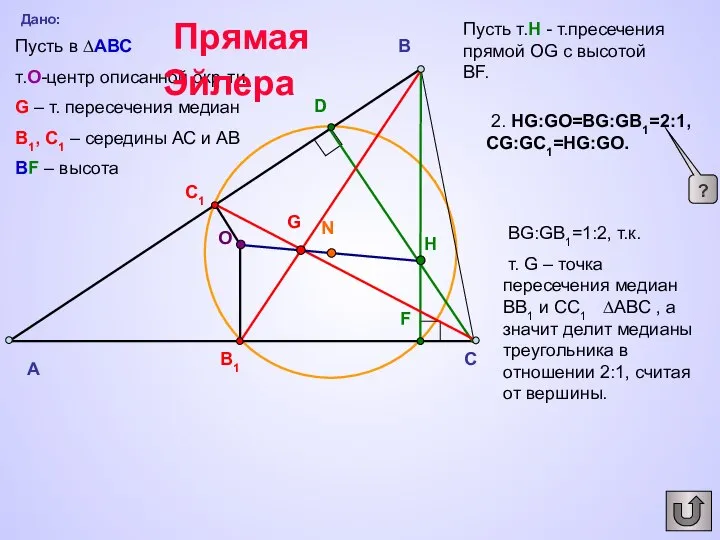
- 22. A C B D F B1 C1 G О N H Дано: Пусть в ∆АВС т.O-центр
- 23. A C B D F B1 C1 G О N H Дано: Пусть в ∆АВС т.O-центр
- 24. A C B D F B1 C1 G О N H Дано: Пусть в ∆АВС т.O-центр
- 25. A C B E D F B1 A1 C1 X Y Z - Середины его сторон
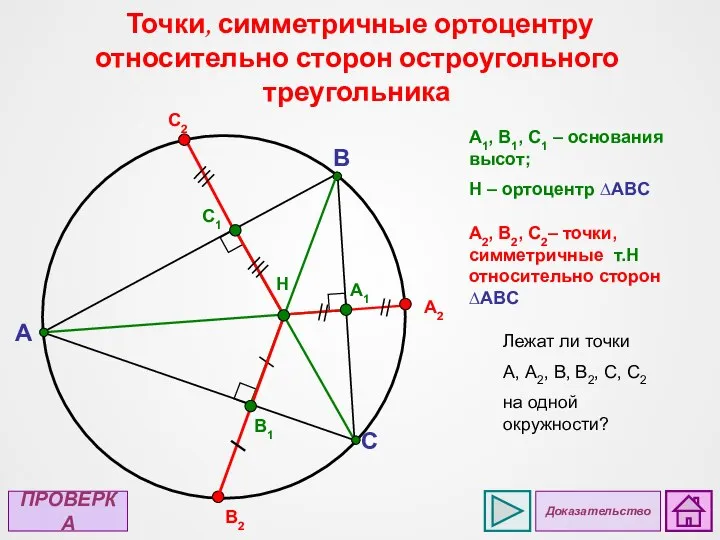
- 26. A C B B1 H A1 C1 А2 C2 B2 Точки, симметричные ортоцентру относительно сторон остроугольного
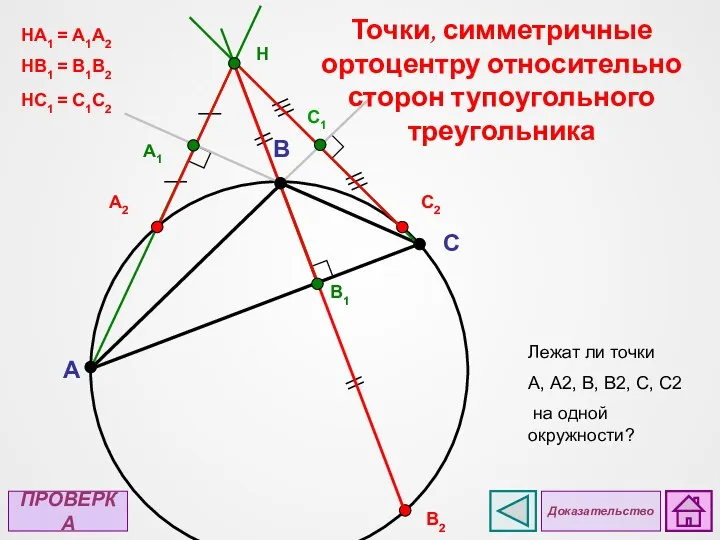
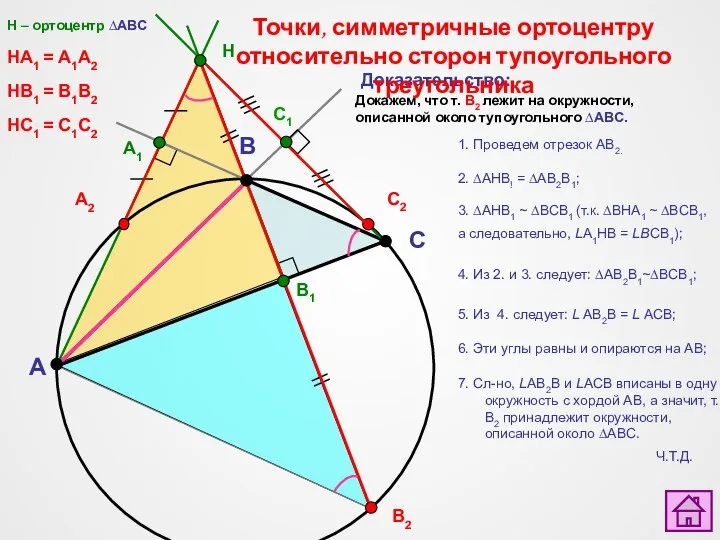
- 27. A C B H A1 В2 B1 А2 C1 C2 Точки, симметричные ортоцентру относительно сторон тупоугольного
- 28. C A1 B D A2 A3 Точка Торричелли
- 29. A B C О P F E D Прямая Симпсона
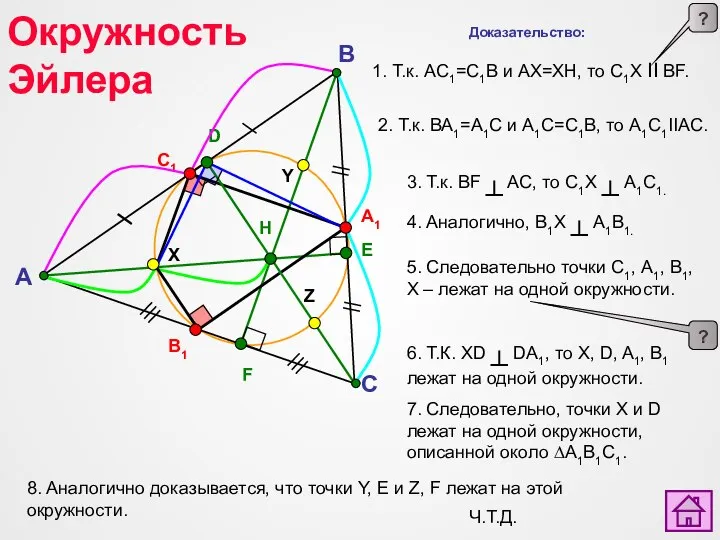
- 30. A C B B1 A1 C1 X Y Z D F E H Окружность Эйлера
- 31. A C B E D F B1 A1 C1 X Y Z G O N H
- 32. A C B E D F B1 A1 C1 X Y Z K3 K1 K2 K
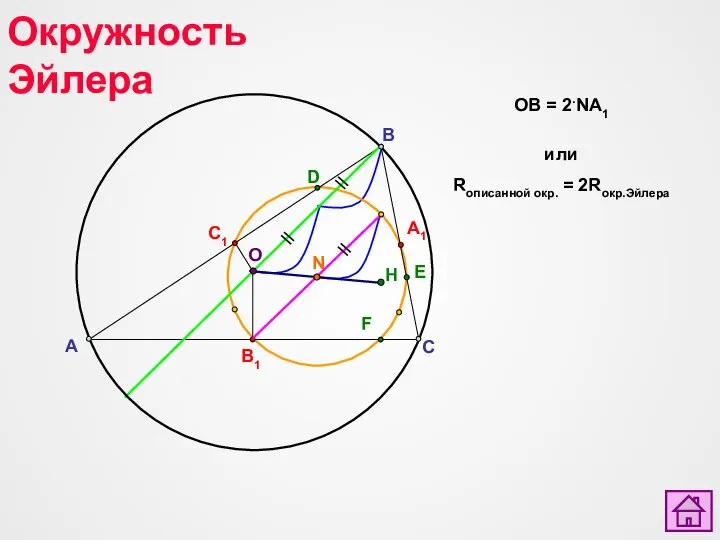
- 33. A C B D F B1 C1 O N H Окружность Эйлера E A1 OB =
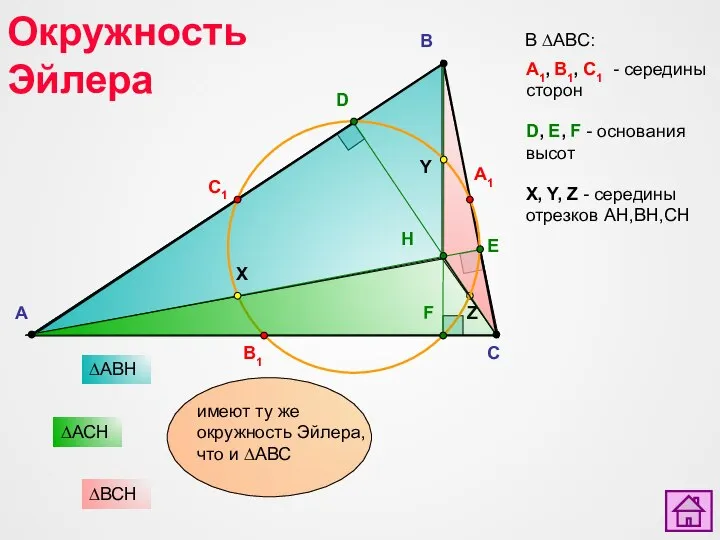
- 34. A C B E D F B1 A1 C1 X Y Z В ∆АВС: Окружность Эйлера
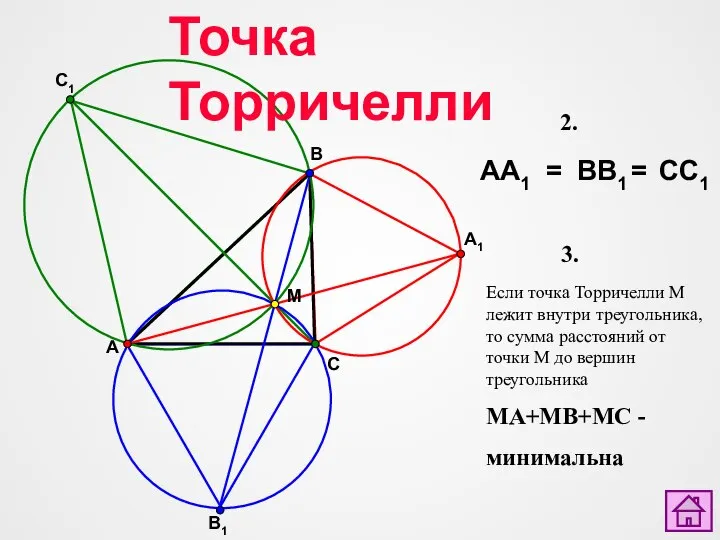
- 35. Точка Торричелли A1 A B1 C1 B C M AA1 BB1 CC1 = = Если точка
- 36. A B C О P F E D F1 E1 D1 H Прямая Симпсона делит отрезок
- 38. Скачать презентацию






 Методика работы с задачей на круговое движение
Методика работы с задачей на круговое движение Обработка оптических изображений. Несколько слов о статистике
Обработка оптических изображений. Несколько слов о статистике Задачи на части
Задачи на части Математическая статистика
Математическая статистика Решение задач геометрия
Решение задач геометрия Відстань між двома точками. Координати середини відрізка
Відстань між двома точками. Координати середини відрізка Геометрические фигуры
Геометрические фигуры Построение графиков функций. Алгебра и начала анализа 11 класс
Построение графиков функций. Алгебра и начала анализа 11 класс Презентация на тему Геометрические тела. Многогранники
Презентация на тему Геометрические тела. Многогранники  Модуль числа
Модуль числа Техника расчёта квадратов целых чисел
Техника расчёта квадратов целых чисел График функции. Задания
График функции. Задания Математика
Математика Признаки параллельности прямых
Признаки параллельности прямых Перпендикуляр и наклонная
Перпендикуляр и наклонная Центральные и вписанные углы
Центральные и вписанные углы Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Длина окружности,
Длина окружности, Теория графов. Основные понятия. Лекция 6
Теория графов. Основные понятия. Лекция 6 Иррациональные неравенства. Неравенства с модулем
Иррациональные неравенства. Неравенства с модулем Метрология: применение математической статистики при измерениях и испытаниях
Метрология: применение математической статистики при измерениях и испытаниях algebr_drobi рабочая презентация начиная с 5 ссентября
algebr_drobi рабочая презентация начиная с 5 ссентября Коммутативность операторов Дункла
Коммутативность операторов Дункла Деление чисел
Деление чисел Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Соотношения между сторонами и углами в произвольном треугольнике
Соотношения между сторонами и углами в произвольном треугольнике Деление дробей
Деление дробей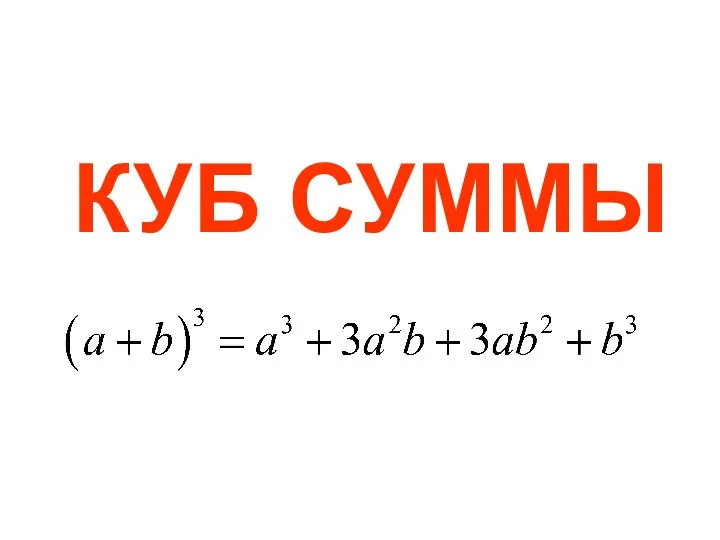 Куб суммы
Куб суммы