Содержание
Слайд 2Преобразование уравнений
Введем относительные переменные, то есть число людей в том или ином
Преобразование уравнений
Введем относительные переменные, то есть число людей в том или ином

Система дифференциальных уравнений приобретает вид:
Коэффициент k=Np характеризует скорость распространения вируса. Из уравнений видно, что скорость распространения зависит не только от «активности» людей, но и от общего количества людей в регионе. Сравните данные по регионам России: https://info-coronavirus.ru/
Полученная система уравнений нелинейная, так что исследовать её можно только численно. Решение зависит как от значений параметров, так и от начальных условий. В качестве начальных условий нужно взять:
где y0 – то, что привезли из заграницы в начальный момент времени
Слайд 3Оценка параметров
Параметр y0 – некоторое небольшое число, например 0,0001
Параметр γ - величина
Оценка параметров
Параметр y0 – некоторое небольшое число, например 0,0001
Параметр γ - величина

Параметр a – относительное число выздоровевших людей. Точных данных по короновирусу нет, но в качестве оценки можно взять значение от 0,95 до 0,99.
Параметр k – самый неопределенный параметр. Разумность его может показать только численный эксперимент который Вам нужно провести. Результаты расчета при некотором (секретном) значении параметра приведены на следующем слайде.
При расчете потребуется ещё один параметр – время окончания расчета. Его также придется подобрать, исходя из того, что при большом значении времени переменные стремятся к некоторым пределам (графики на следующем слайде).
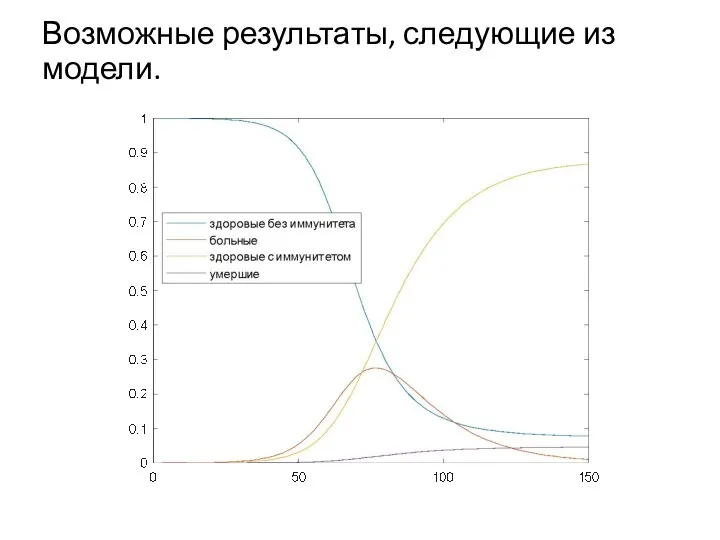
Слайд 4Возможные результаты, следующие из модели.
Возможные результаты, следующие из модели.
 Аналитический отчет акушерско-гинекологической службы УЗ 3-я городская клиническая больница им. Е.В. Клумова
Аналитический отчет акушерско-гинекологической службы УЗ 3-я городская клиническая больница им. Е.В. Клумова Санитарное просвещение Правила личной гигиены для детей
Санитарное просвещение Правила личной гигиены для детей Анатомо-фізіологічні особливості шкіри, підшкірної клітковини і лімфатичних вузлів у дітей
Анатомо-фізіологічні особливості шкіри, підшкірної клітковини і лімфатичних вузлів у дітей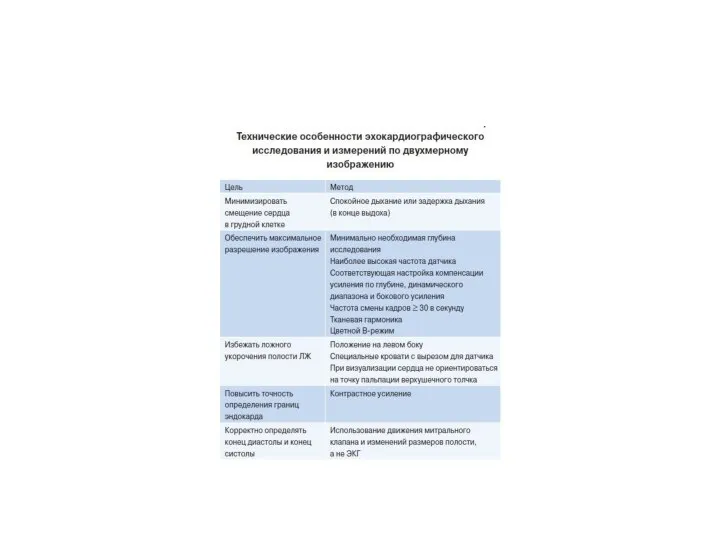 Структура эхокардиографического исследования
Структура эхокардиографического исследования История мануальной медицины
История мануальной медицины Главные заповеди здорового образа жизни
Главные заповеди здорового образа жизни Адаптация к охлаждающему воздействию
Адаптация к охлаждающему воздействию Клуб будущих и молодых мам Саратова. Упражнения Кегеля. Попеременная релаксация. Аффирмации
Клуб будущих и молодых мам Саратова. Упражнения Кегеля. Попеременная релаксация. Аффирмации Қазақстанда еңбек төлемдерінің жаңа жүйесін ендіру
Қазақстанда еңбек төлемдерінің жаңа жүйесін ендіру Формирование групп риска по развитию рака яичников после прохождения процедуры ЭКО
Формирование групп риска по развитию рака яичников после прохождения процедуры ЭКО Гастроэзофагеальная рефлюксная болезнь
Гастроэзофагеальная рефлюксная болезнь (1)
(1) Профилактика онкологических заболеваний
Профилактика онкологических заболеваний Сексуальная функция и менопауза
Сексуальная функция и менопауза МДК02.03 Л21 № 3 ч.2 акушеркам А21 Основы трансфузиологии
МДК02.03 Л21 № 3 ч.2 акушеркам А21 Основы трансфузиологии Пищевое отравление и микотоксикозы
Пищевое отравление и микотоксикозы Понятие о ВИЧ инфекции и СПИДЕ
Понятие о ВИЧ инфекции и СПИДЕ Принципы рациональной антибиотикотерапии
Принципы рациональной антибиотикотерапии Острый коронарный синдром и острые заболевания пищевода и желудка
Острый коронарный синдром и острые заболевания пищевода и желудка ІХС: Інфаркт міокарда
ІХС: Інфаркт міокарда Методика кормления тяжелобольных пациентов
Методика кормления тяжелобольных пациентов Денсаулық практикасы үшін инсулин алудың тәсілі
Денсаулық практикасы үшін инсулин алудың тәсілі 1 (11)
1 (11) Порядок оказания медицинской помощи взрослому населению при заболеваниях глаз, его придаточного аппарата и орбиты
Порядок оказания медицинской помощи взрослому населению при заболеваниях глаз, его придаточного аппарата и орбиты Ветеринарная микробиология и микология
Ветеринарная микробиология и микология СРС ЭКГ-диагностика нарушений ритма сердца
СРС ЭКГ-диагностика нарушений ритма сердца Первичное здоровье
Первичное здоровье Նորք-մարաշ բժշկական կենտրոն
Նորք-մարաշ բժշկական կենտրոն