Содержание
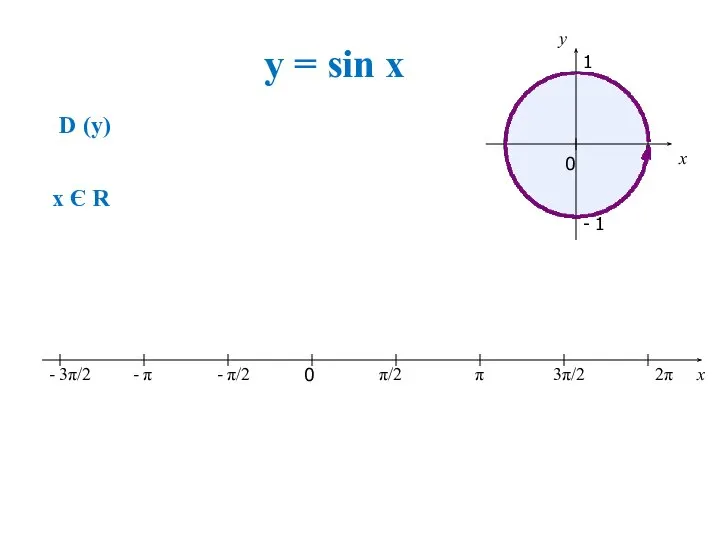
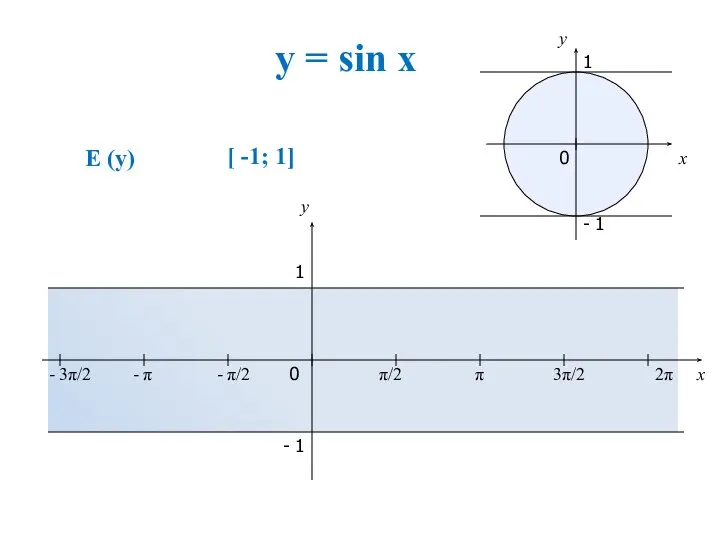
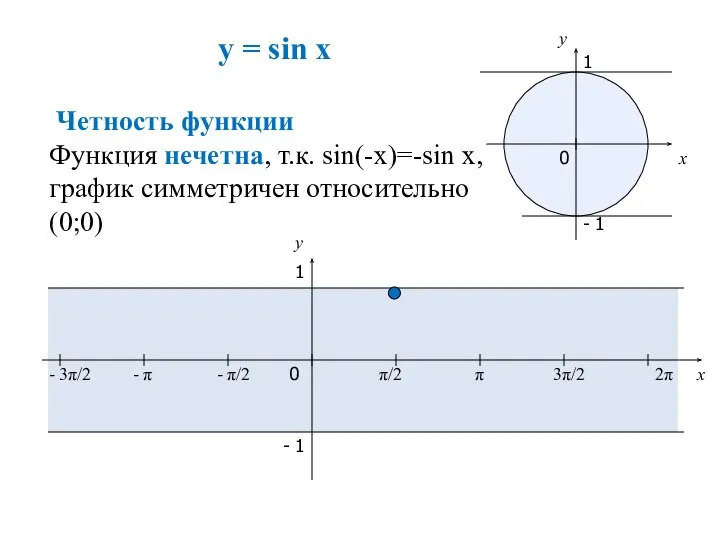
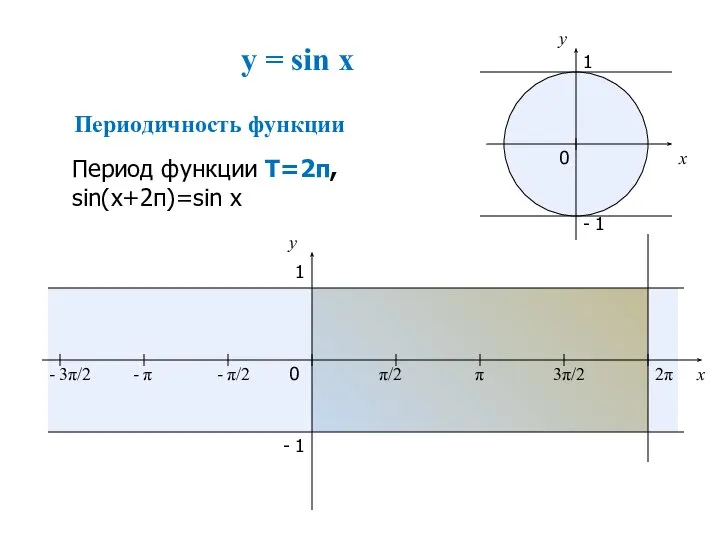
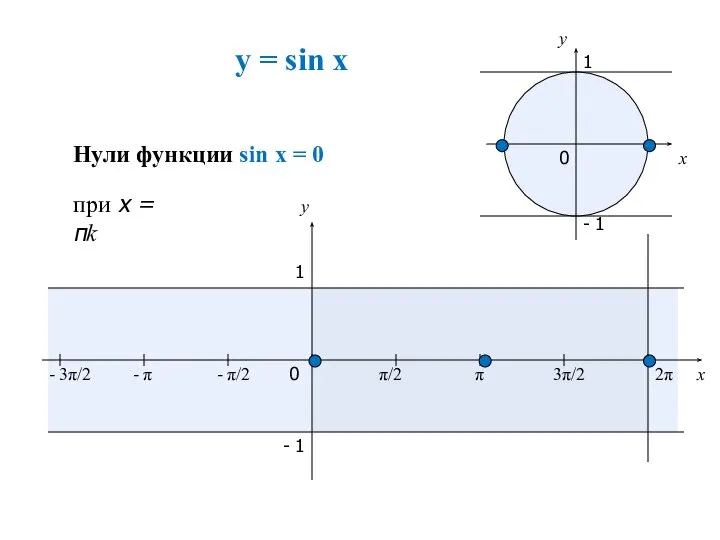
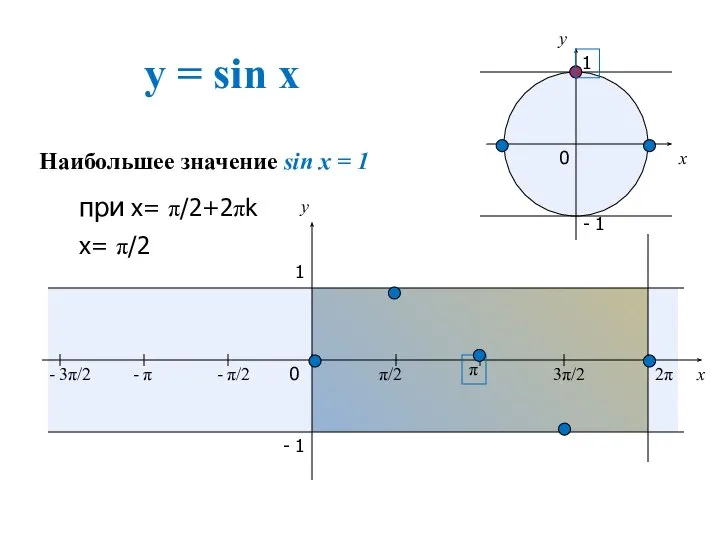
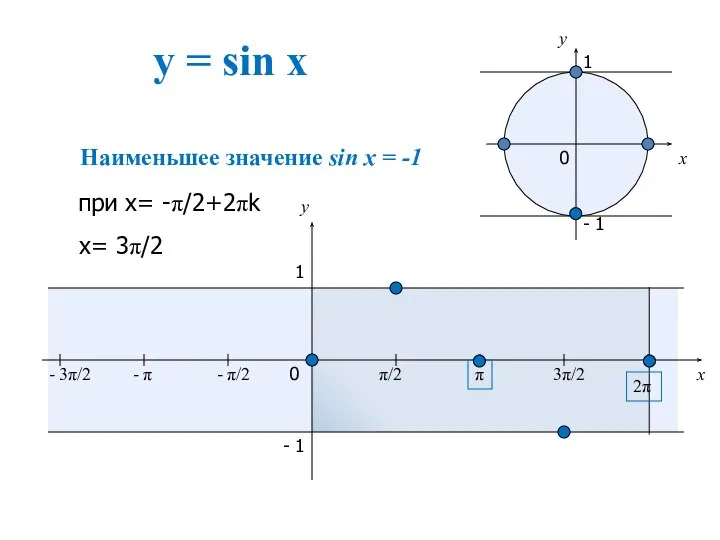
- 2. Свойства функции 1.D(y) 2.E(y) 3. Четность функции 4. Периодичность функции 5.Нули функции 6. Наибольшее значение 7.
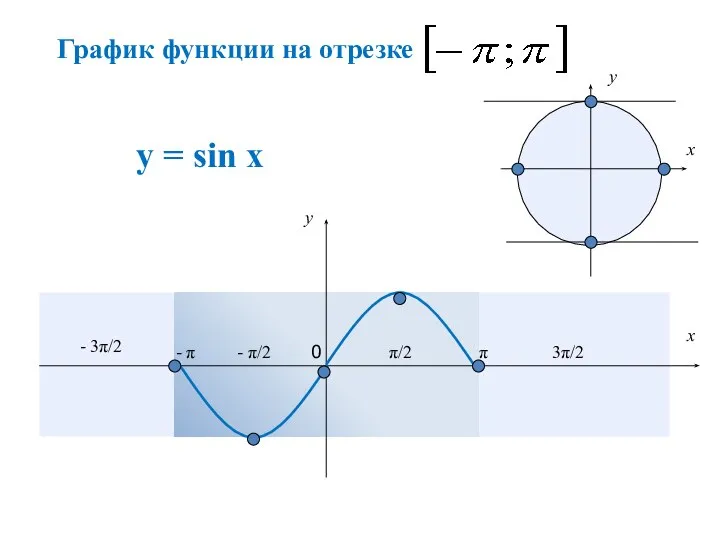
- 3. y = sin x x 0 π/2 π 3π/2 2π - π/2 - π - 3π/2
- 4. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 5. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 6. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 7. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 8. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 9. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
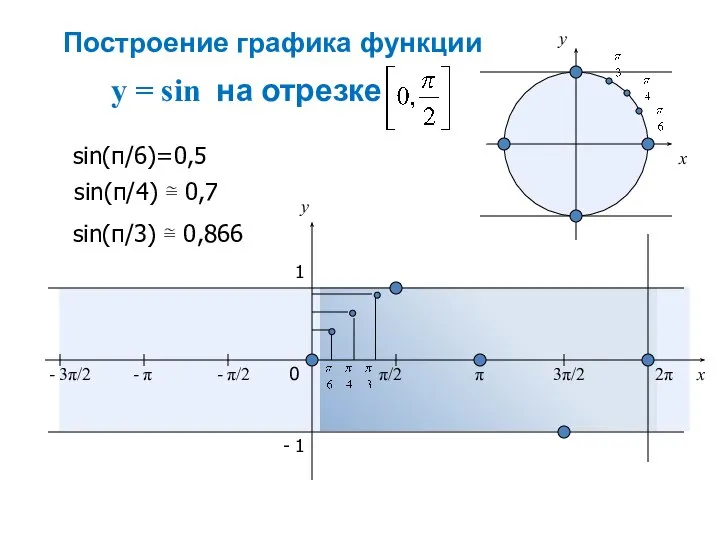
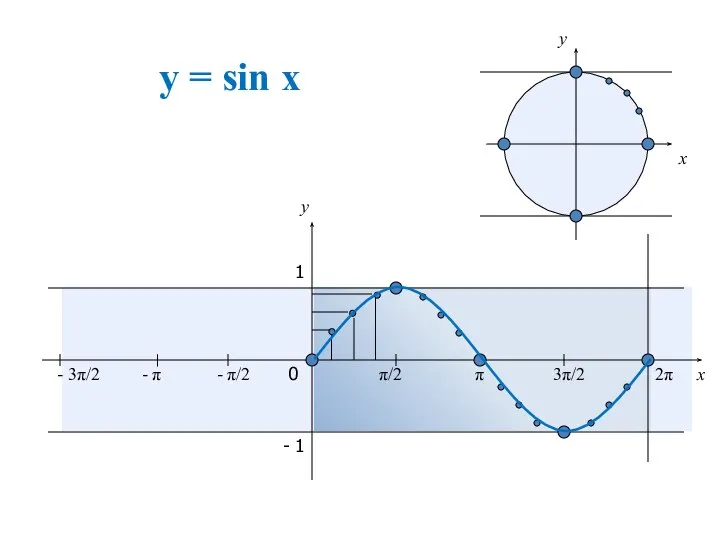
- 10. y = sin на отрезке x y 0 π/2 π 3π/2 2π x y 1 -
- 11. у = sin x π π/2 - π/2 - π - 3π/2 3π/2 y x 0
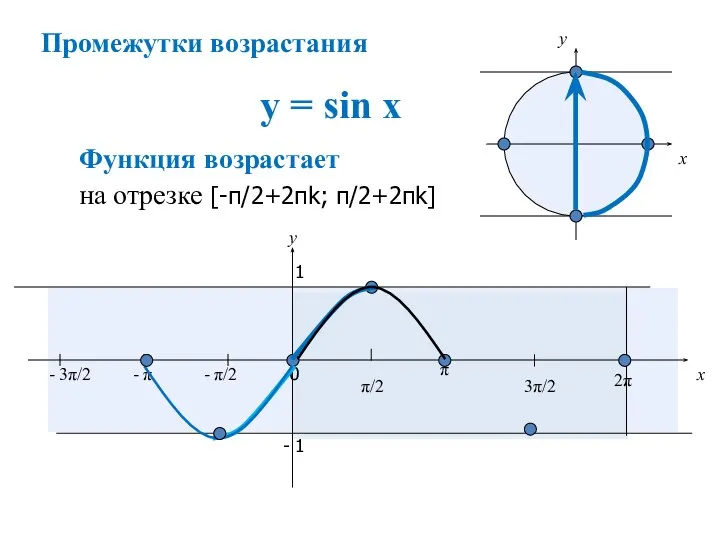
- 12. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
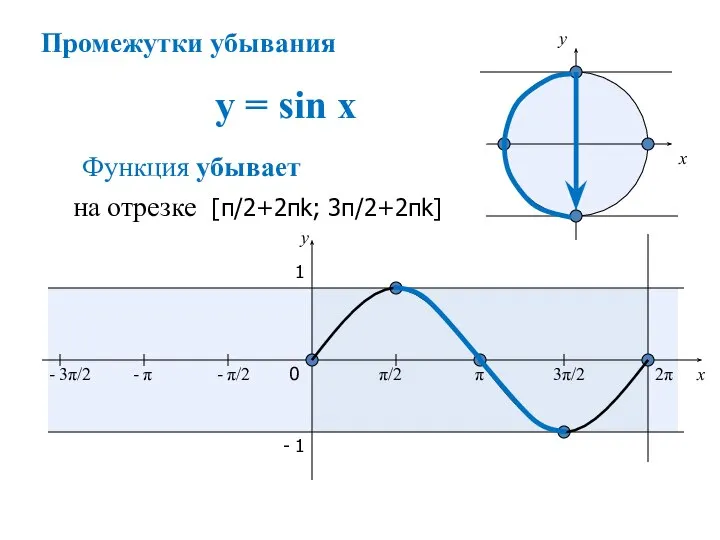
- 13. y = sin x x y 0 π/2 π 3π/2 2π 1 - 1 - π/2
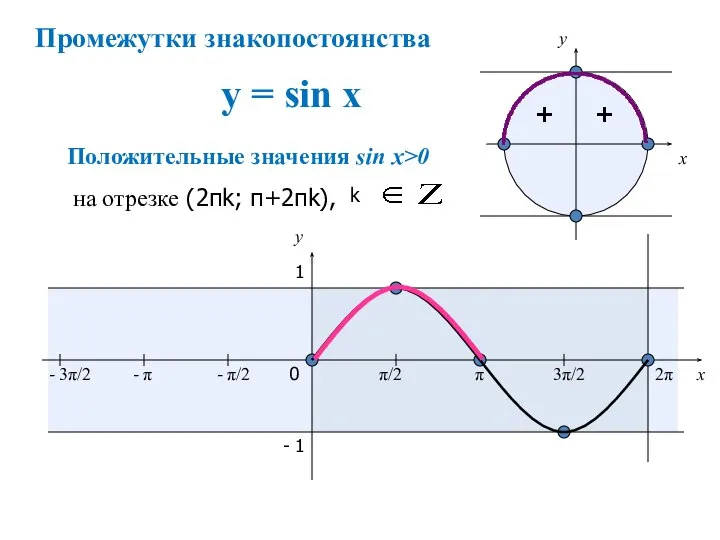
- 14. y = sin x + + x y 0 π/2 π 3π/2 2π x y 1
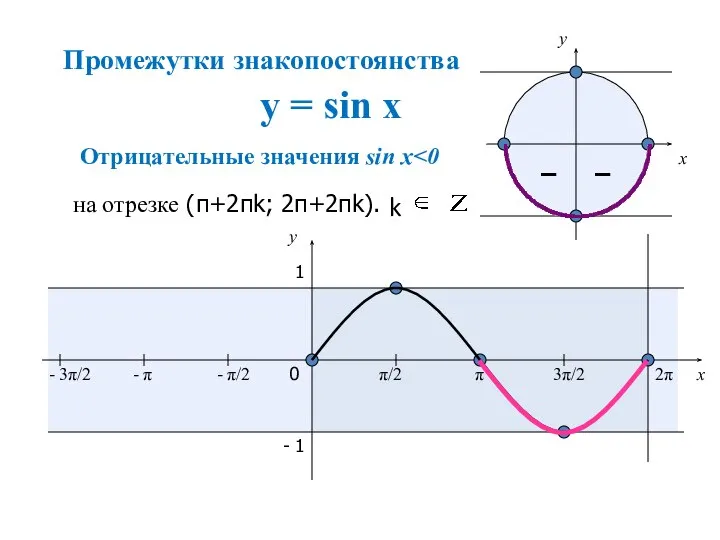
- 15. y = sin x – – x y 0 π/2 π 3π/2 2π x y 1
- 16. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 17. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 18. Сравнить числа sin 2 и sin 3 Задача Так как = 3,14, , то Из графика
- 19. Упражнения Пользуясь свойствами функции у = sin x , сравните числа: sin 1000 и sin 1300
- 20. Расположить в порядке возрастания числа sin 1.9 ; sin 3; sin(-1); sin(-1.5). Числа sin 1.9 и
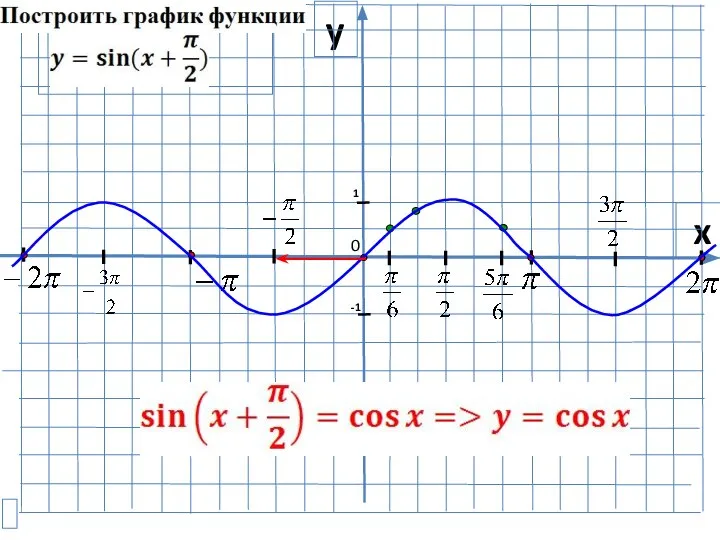
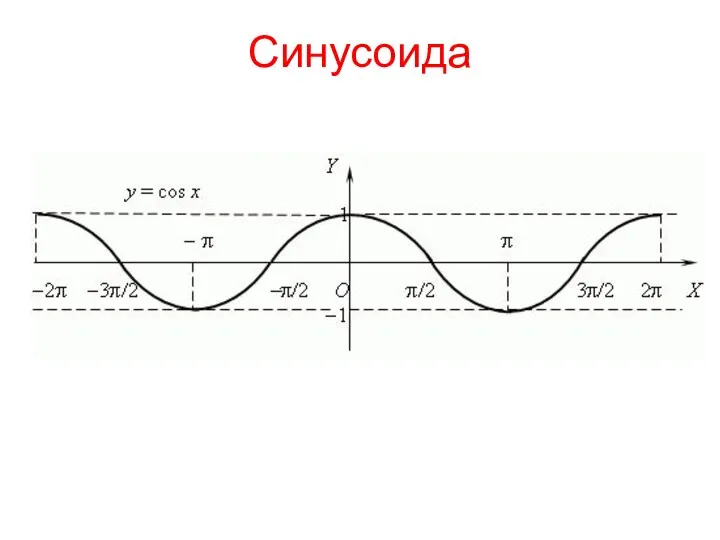
- 21. Функция y=cosx, ее свойства и график
- 22. 0
- 23. Свойства функции 1. D(f) = R 2. Функция y=cosx – четная, так как cos(-x) = cosx
- 24. 4. Функция y=cosx ограничена снизу и сверху, т.е. ограничена: -1 ≤ cost ≤ 1 5.
- 25. 6. Функция y=cosx – непрерывная функция. 7. E(f) = [-1;1].
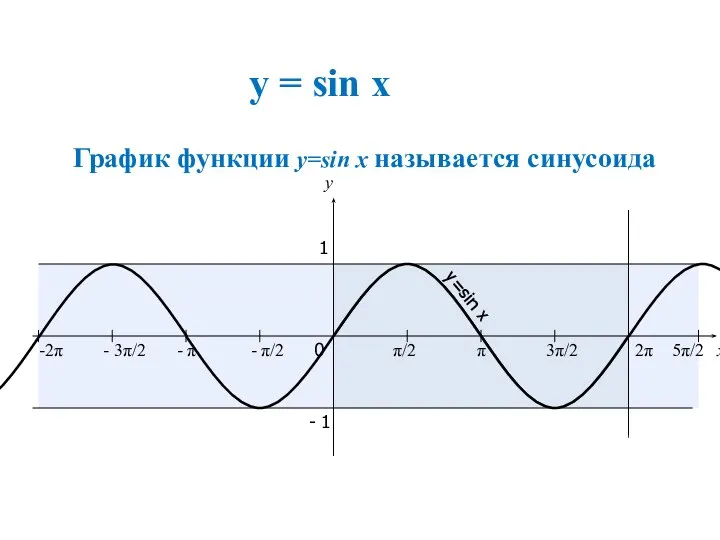
- 26. Синусоида
- 28. Скачать презентацию







![6. Функция y=cosx – непрерывная функция. 7. E(f) = [-1;1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1107643/slide-24.jpg)
 Окружность. Вписанные и описанные углы
Окружность. Вписанные и описанные углы Матрицы
Матрицы Презентация на тему Натуральные числа 5 класс
Презентация на тему Натуральные числа 5 класс  Свойства сложения и умножения - Презентация_
Свойства сложения и умножения - Презентация_ Симметрия в окружающем нас мире
Симметрия в окружающем нас мире Площадь четырехугольника
Площадь четырехугольника Составление объемных фигур из отдельных элементов кубиков Сома
Составление объемных фигур из отдельных элементов кубиков Сома Перестановки. Размещения
Перестановки. Размещения chislo-pi
chislo-pi В мире чисел и цифр
В мире чисел и цифр ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Тренировочные задания В2 (графическое представление данных)
Тренировочные задания В2 (графическое представление данных) Элементы комбинаторики
Элементы комбинаторики Подготовка к ГИА. Задачи
Подготовка к ГИА. Задачи Касательная к окружности
Касательная к окружности Расчет нормированных приоритетов
Расчет нормированных приоритетов Приемы письменных вычислений
Приемы письменных вычислений Векторы. Обобщающий урок
Векторы. Обобщающий урок Величины и их измерение. Длина
Величины и их измерение. Длина Понятие цилиндра
Понятие цилиндра Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Лекция 2
Лекция 2 Презентация Понономарев
Презентация Понономарев Геометрия (8 класс)
Геометрия (8 класс) Статистика и дизайн информации
Статистика и дизайн информации Решение систем уравнений и неравенств графическим способом
Решение систем уравнений и неравенств графическим способом Определители матриц
Определители матриц Письмо от президента Клуба серьёзных математиков
Письмо от президента Клуба серьёзных математиков