Полногеномный анализ ассоциаций

GWAS
Полногено́мный анализ ассоциа́ций (англ. GWAS, Genome-Wide Association Studies) — направление биологических (как правило, биомедицинских) исследований, связанных с исследованием ассоциаций между геномными вариантами и фенотипическими признаками. Часто под полногеномным анализом ассоциаций подразумевают только поиск связей между однонуклеотидными полиморфизмами и заболеваниями человека, однако термин употребим и к другим организмам.
(Википедия)

GWAS
Обычно сравнивают геномы группы больных людей с геномами контрольной группы, включающей в себя аналогичных по возрасту, полу и другим признакам здоровых людей. Материалом для исследования являются образцы ДНК каждого участника исследования. Если удается выявить варианты геномов (точнее, совокупность аллелей), которые значимо чаще встречаются у людей с данным заболеванием, то говорят, что такой вариант связан, или ассоциирован, с болезнью. В отличие от методов, которые проверяют один или несколько конкретных участков генома, полногеномный поиск ассоциаций использует полную последовательность ДНК. Следует отметить, что этот подход к исследованиям не выявляет мутации, ставшие причиной заболевания, а только более или менее значительную корреляцию с заболеванием или другим признаком
(Википедия)

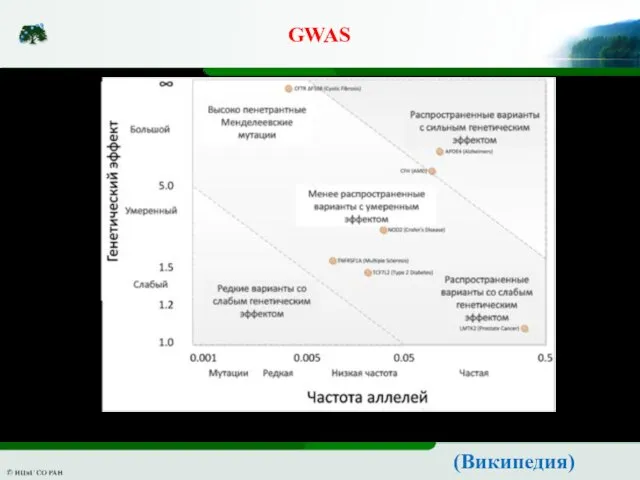
GWAS
(Википедия)
Вторая по важности область применения GWAS — фармакогенетика, то есть поиск аллелей, связанных с метаболизмом лекарственных препаратов и их побочными эффектами.
Первые успешные исследования полногеномных ассоциаций были проведены на больных макулодистрофией и опубликованы в 2005 году. Были обнаружены два аутосомных однонуклеотидных полиморфизма. К 2011 году были протестированы сотни тысяч людей, было проведено более 1200 исследований полногеномных ассоциаций для 200 заболеваний и фенотипических проявлений, в результате было найдено около 4000 однонуклеотидных полиморфизмов. Ряд исследований полногеномных ассоциаций был раскритикован за пренебрежение контролем качества. В целом методология до сих пор является предметом для споров.

GWAS
(Википедия)
В основе поиска полногеномных ассоциаций как правило лежит сравнение геномов двух групп людей: носителей исследуемого фенотипа (заболевания) и контрольной группы. Для всех индивидуумов производится генотипирование для большинства известных однонуклеотидных полиморфизмов (SNP). Далее, для каждого SNP проверяется, насколько значимы различия в распределении частот аллелей между исследуемой и контрольной группой.
Альтернативой делению на две группы в полногеномных исследованиях является количественный анализ фенотипа, например, рост, концентрация биомаркера или экспрессия гена. Кроме того, могут быть использованы данные о пенетрантности исследуемых аллелей.

GWAS
(Википедия)

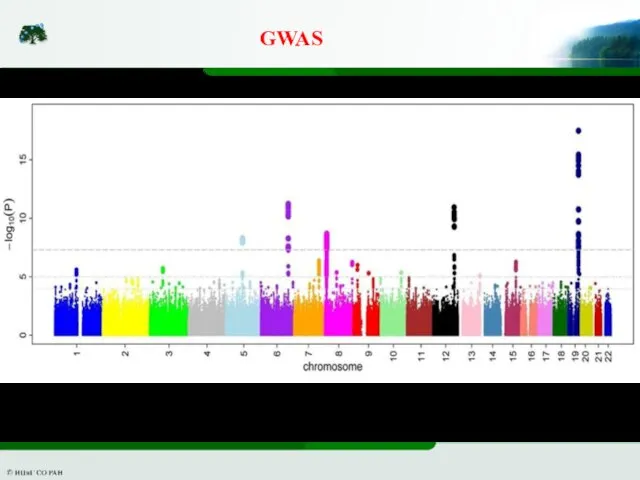
GWAS
Верхняя прямая − критерий Бонферрони, нижняя − FDR

Если нам нужно сравнить средние двух заданных групп, обычно используется t-критерий Стьюдента или Уэлша. Если число групп больше двух, используется F-критерий Фишера (ANOVA).
Распределение значений внутри групп предполагается нормальным. Строго говоря, только при справедливости этого предположения можно использовать t- или F-критерий.

На самом деле нормальность распределения требуется не для самих выборок, а только для их средних, а они всегда распределены приближенно нормально для любых распределений даже при небольших N в силу центральной предельной теоремы.

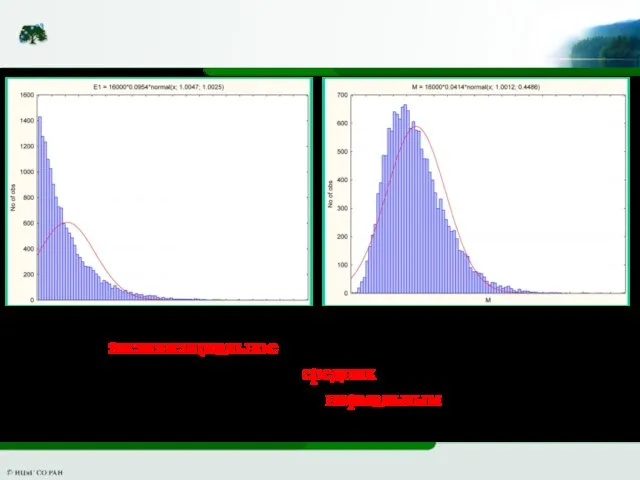
Слева: экспоненциальное распределение (λ=1). Справа: распределение выборочных средних из него объема n=10. Красная кривая: аппроксимация нормальным распределением.

Нулевая гипотеза заключается в том, что различия между выборками являются случайными и все выборки на самом деле взяты из одного и того же генерального распределения.
Если значения рассчитанного критерия превышают табличные значения для заданного уровня значимости α (0.05; 0.01; 0.001), то мы считаем, что нулевая гипотеза не подтверждается. Это ошибка первого рода.

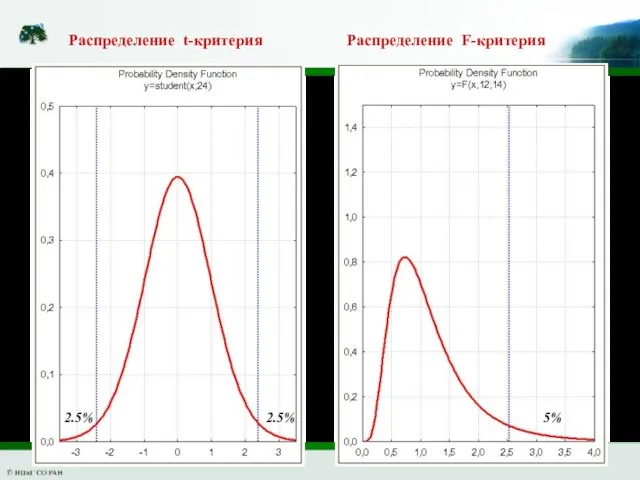
Распределение t-критерия Распределение F-критерия
2.5%
2.5%
5%

Но это верно для одного эксперимента. Если эксперимент повторяется N раз, то вероятность, что хотя бы один выборочный критерий случайно превысит табличный уровень, равна 1-(1-α)N. Если мы хотим гарантировать, что с вероятностью α ни один из N рассчитанных критериев не превысит табличный уровень, то мы должны выбрать табличный уровень, равный α/N. Это критерий Бонферрони.

Этот критерий слишком жесткий. Если, например, α= 0.05 и N= 106, то p= α/N= 5∙10-8
и lg(p)= -7.301.
Через критерий Бонферрони проходит слишком мало полезной информации. Поэтому в 1995 году Бенджамини и Хохберг предложили критерий FDR (False Discovery Rate). Этот критерий сейчас, например, является основным в микрочиповых исследованиях.

Критерий FDR заключается в следущем. Произвольно выбираем уровень значимости p. Ожидаемое число случайных выборочных критериев, которые должны превысить соответствующее p табличное значение tp, равно pN. Мы сравниваем это число с k -- реальным числом выборочных критериев, превысивших tp. Если pN достаточно мало по сравнению с k, например, меньше 5%, то tp в качестве порогового значения нас вполне устраивает.
FDR (false discovery rate)

FDR (false discovery rate)
(N=106)

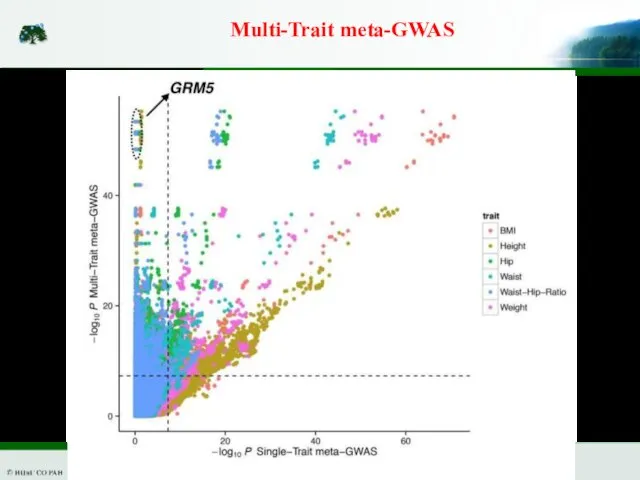
Multi-Trait meta-GWAS

Спасибо за внимание!
Thank you for your attention!
感谢您的关注！

GWAS