Содержание
- 2. 10 класс Урок-расследование Дело №0377 о похищении полосатого слона
- 4. Для какого из указанных значений Х истинно высказывание: 1) 1 2) 2 3) 3 4) 4
- 5. Сейф, в котором хранится рыбий жир и флейта, надежно защищен кодом. Но преступники в двух шагах
- 6. И какой же детектив обходится без погони?!
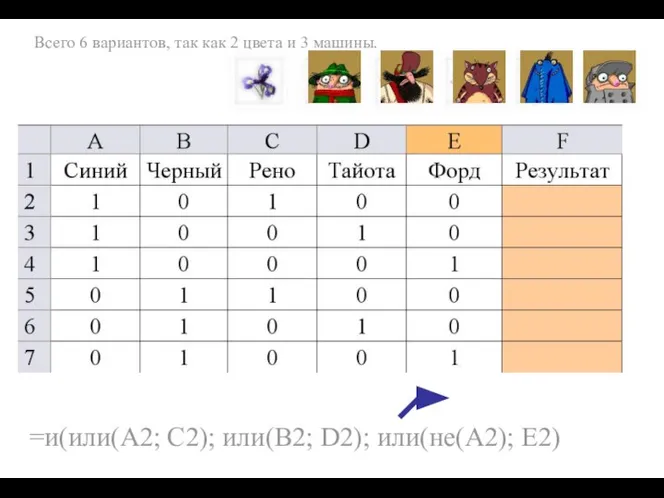
- 7. - Это был синий Рено. - По-моему, черная Тайота. -Ну, уж точно не синий Форд .
- 8. Всего 6 вариантов, так как 2 цвета и 3 машины. =и(или(А2; С2); или(В2; D2); или(не(А2); Е2)
- 10. Б2 У1 Л0 Ь5 М3 С4 К6
- 11. Джордж Буль (2 ноября 1815 - 8 декабря 1864) английский математик и логик, один из основоположников
- 12. Самостоятельная работа. Расположите изученные логические функции в порядке их выполнения. 2. Чему равно значение предиката третьего
- 14. Скачать презентацию










 Блок занятий по развитию сенсорного восприятия Играющий луч для детей дошкольного возраста с ОВЗ
Блок занятий по развитию сенсорного восприятия Играющий луч для детей дошкольного возраста с ОВЗ Сказка про лису - рыжую красу
Сказка про лису - рыжую красу Цветок на основе модуля оригами. Цветок для мамы
Цветок на основе модуля оригами. Цветок для мамы Муниципальный конкурс Полезная прогулка. Средняя группа
Муниципальный конкурс Полезная прогулка. Средняя группа Удивительные профессии
Удивительные профессии Шаблон (пример) к очному этапу
Шаблон (пример) к очному этапу Все, что осень подарила. Познавательное мероприятие
Все, что осень подарила. Познавательное мероприятие Особенности адаптации младшего школьника
Особенности адаптации младшего школьника Программно-методическое обеспечение образовательного процесса в работе педагога дополнительного образования
Программно-методическое обеспечение образовательного процесса в работе педагога дополнительного образования День Матери. Поздравляем маму
День Матери. Поздравляем маму Накопление лингвопедагогических представлений в развитии правильной речи у детей (педагогические истоки)
Накопление лингвопедагогических представлений в развитии правильной речи у детей (педагогические истоки) Методическое портфолио
Методическое портфолио Проведение уроков изобразительного искусства с применением здоровьесберегающих технологий
Проведение уроков изобразительного искусства с применением здоровьесберегающих технологий Я патриот своего папы
Я патриот своего папы Создание художественного образа с использованием нетрадиционных материалов
Создание художественного образа с использованием нетрадиционных материалов Наблюдение как основной метод педагогической диагностики
Наблюдение как основной метод педагогической диагностики Признаки весны
Признаки весны Волшебный мир бисера
Волшебный мир бисера Выставка работ воспитанников, посвящённая 60-летию первого полёта человека в Космос
Выставка работ воспитанников, посвящённая 60-летию первого полёта человека в Космос Гиперактивный ребенок
Гиперактивный ребенок Познавательно-исследовательская деятельность в детском саду
Познавательно-исследовательская деятельность в детском саду Театр и игра в жизни дошкольников
Театр и игра в жизни дошкольников Волкова Н.А. Угадай-ка Грибы и ягоды. Игра для детей 5-7 лет
Волкова Н.А. Угадай-ка Грибы и ягоды. Игра для детей 5-7 лет Практические рекомендации родителям по развитию внимания ребёнка
Практические рекомендации родителям по развитию внимания ребёнка Автоматизация звука [Ж] в слогах
Автоматизация звука [Ж] в слогах лекция 4 методы, формы, виды уроков
лекция 4 методы, формы, виды уроков Здравствуй Осень
Здравствуй Осень Варианты концертной программы для Дня урожая
Варианты концертной программы для Дня урожая