Содержание
- 2. 1 Поняття похибки Похибка результату вимірювання — це відхилення результату вимірювань (Хизм) від істинного (дійсного) значення
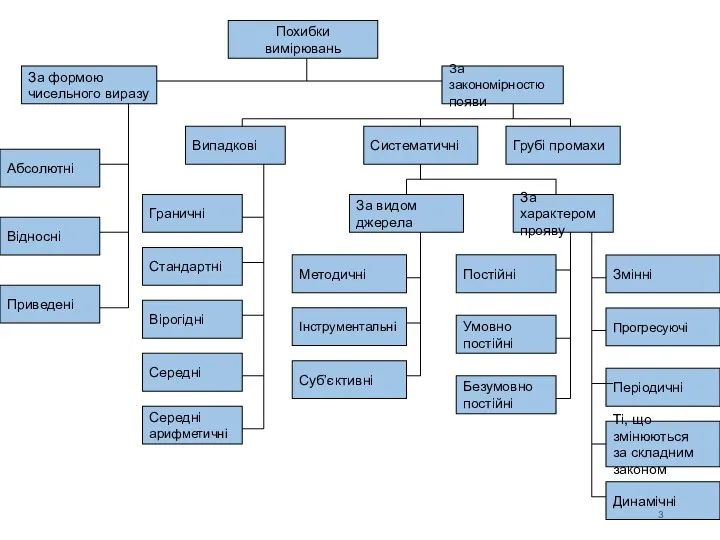
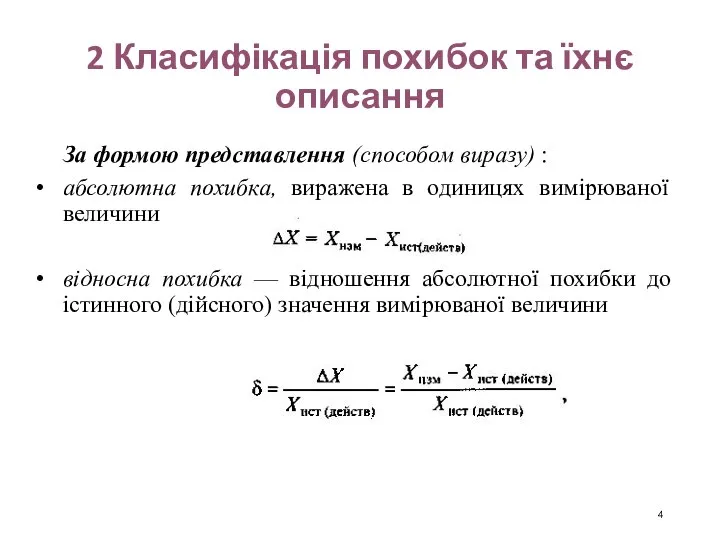
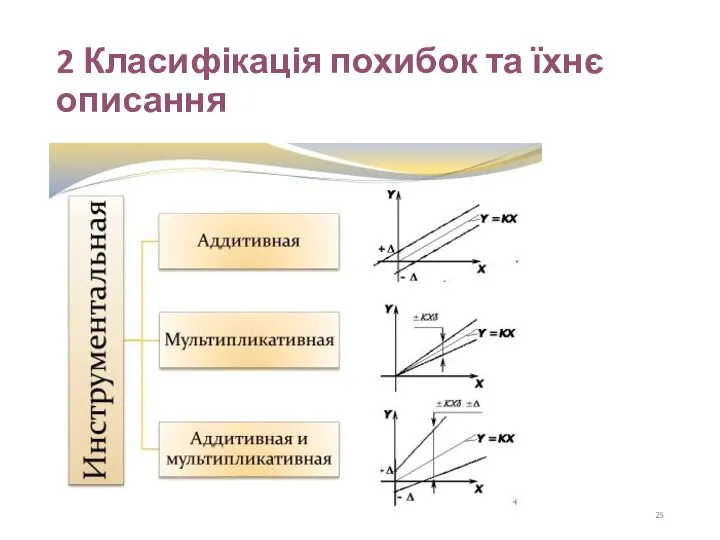
- 4. 2 Класифікація похибок та їхнє описання За формою представлення (способом виразу) : абсолютна похибка, виражена в
- 5. 2 Класифікація похибок та їхнє описання Похибка засобів вимірювань обчислюється за формулою: де Хп — показ
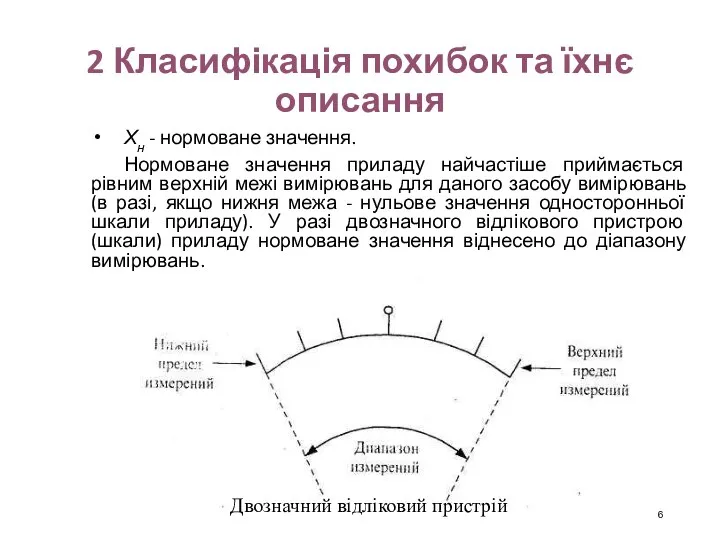
- 6. 2 Класифікація похибок та їхнє описання Хн - нормоване значення. Нормоване значення приладу найчастіше приймається рівним
- 7. 2 Класифікація похибок та їхнє описання В якості істинного значення при багаторазових вимірах одного і того
- 8. 2 Класифікація похибок та їхнє описання Величина X, отримана в одній серії вимірювань, є випадковим наближеннням
- 9. 2 Класифікація похибок та їхнє описання Для оцінки розсіювання одиничних результатів вимірювань в ряду рівноточних вимірювань
- 10. 2 Класифікація похибок та їхнє описання при п > 20 СКВ із серії вимірювань завжди менше,
- 11. 2 Класифікація похибок та їхнє описання За характером прояву похибки поділяються на систематичні і випадкові. Систематична
- 12. 2 Класифікація похибок та їхнє описання В залежності від характера вимірювання систематичні похибки поділяють на постійні,
- 13. 2 Класифікація похибок та їхнє описання Прогресуючі похибки — це безперервно зростаючі або спадаючі похибки. Вони
- 14. 2 Класифікація похибок та їхнє описання
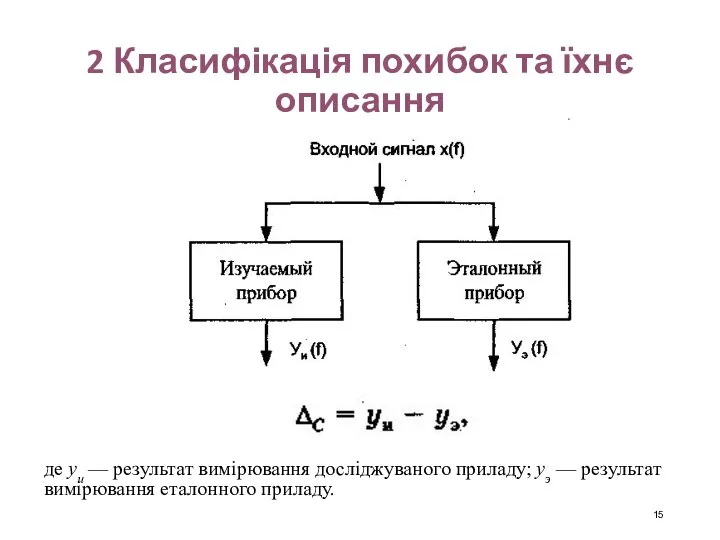
- 15. 2 Класифікація похибок та їхнє описання де уи — результат вимірювання досліджуваного приладу; уэ — результат
- 16. 2 Класифікація похибок та їхнє описання Випадковими називаються похибки, що змінюються випадковим чином (по знаку і
- 17. 2 Класифікація похибок та їхнє описання Величина випадкової похибки Δсл характеризує третій показник якості вимірювань –
- 18. 2 Класифікація похибок та їхнє описання За умовами проведення вимірювань похибки засобів вимірювань поділяються на основні
- 19. 2 Класифікація похибок та їхнє описання Значення похибок засобів вимірювань, що експлуатуються в умовах, що відрізняються
- 20. 2 Класифікація похибок та їхнє описання У більшості нормативно-технічних документів на засоби вимірювань за нормальні значення
- 21. 2 Класифікація похибок та їхнє описання За причиною виникнення похибки поділяються на інструментальні, методичні і суб’єктивні.
- 22. 2 Класифікація похибок та їхнє описання Методична похибка обумовлена недосконалістю і недоліками застосовуваного в засобі вимірювань
- 23. 2 Класифікація похибок та їхнє описання За характером вимірювання фізичної величини похибки засобів вимірювань поділяються на
- 24. 2 Класифікація похибок та їхнє описання За характером залежності від вимірюваної величини Х розрізняють похибки адитивні
- 25. 2 Класифікація похибок та їхнє описання
- 26. 3. Закономірності формування результату вимірювань Правила підсумовування складових похибки. Визначення сумарної систематичної похибки. Межі сумарної систематичної
- 27. 3. Закономірності формування результату вимірювань Коефіцієнт Кр залежить від довірчої ймовірності Р і від числа складових,
- 28. 3. Закономірності формування результату вимірювань Визначення сумарної випадкової складової похибки. (У тому випадку, коли є кілька
- 29. 3. Закономірності формування результату вимірювань Визначення загальної похибки результату вимірювань з урахуванням сумарної систематичної і суммарної
- 30. 3. Закономірності формування результату вимірювань то невиключеними систематичними похибками нехтують і в якості границь загальної похибки
- 31. 3. Закономірності формування результату вимірювань
- 32. 3. Закономірності формування результату вимірювань
- 33. 3. Закономірності формування результату вимірювань Правила округлення значення похибки і записи результату вимірювань. Похибка результату вимірів
- 34. 3. Закономірності формування результату вимірювань Результат вимірювання округлюється до того ж десяткового розряду, яким закінчується округлене
- 35. 3. Закономірності формування результату вимірювань Округлення слід виконувати відразу до бажаного числа значущих цифр, поетапне округлення
- 36. 3. Закономірності формування результату вимірювань Якщо перша (рахуючи зліва направо) з тих, що замінюються нулями або
- 37. 3. Закономірності формування результату вимірювань Особливо уважно слід відноситися до запису результату вимірювання без зазначення похибки,
- 38. 4 Алгоритми обробки багатократних вимірювань Алгоритм обробки прямих багатократних вимірювань виправляють результати спостережень виключенням систематичної похибки;
- 39. 4 Алгоритми обробки багатократних вимірювань виключають промахи; визначають закон розподілу випадкової складової; при заданому значенні довірчої
- 40. 4 Алгоритми обробки багатократних вимірювань Якщо величина Δслуч порівняна з абсолютним значенням похибки ЗВ ΔЗВ, то
- 42. Скачать презентацию

























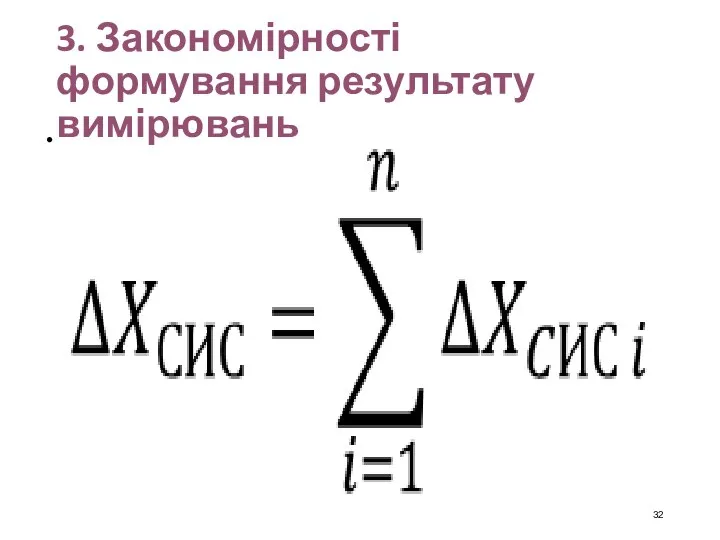








 Интерактивные технологии контроля результатов обучения. Лекция 8
Интерактивные технологии контроля результатов обучения. Лекция 8 Медиакомпетентность педагога как условие развития цифровой образовательной среды
Медиакомпетентность педагога как условие развития цифровой образовательной среды Естественнонаучное пятиборье
Естественнонаучное пятиборье Новогодние игрушки из конусов
Новогодние игрушки из конусов Пафос и логос в речи
Пафос и логос в речи Осенняя пора в жизни растений. Почему желтеют и опадают листья
Осенняя пора в жизни растений. Почему желтеют и опадают листья Карта желаний для марафона
Карта желаний для марафона Уакыттын бос өткені... 7 класс
Уакыттын бос өткені... 7 класс Информирование о программе наставничества
Информирование о программе наставничества Мастера маскировки. Правила игры
Мастера маскировки. Правила игры Виды и формы воспитательной деятельности: методики и технологии
Виды и формы воспитательной деятельности: методики и технологии Презентация на тему Гендерное воспитание в младшем дошкольном возрасте
Презентация на тему Гендерное воспитание в младшем дошкольном возрасте  Развитие связной устной речи на уроках природоведения, географии
Развитие связной устной речи на уроках природоведения, географии Группы раннего эстетического развития Ритмика и танец
Группы раннего эстетического развития Ритмика и танец Влажнотепловая обработка швейных изделий
Влажнотепловая обработка швейных изделий Открытка Панда ко дню матери
Открытка Панда ко дню матери Путешествие с паровозиком по музыкальным станциям Для участников театра эстрадной детской песни Радуга
Путешествие с паровозиком по музыкальным станциям Для участников театра эстрадной детской песни Радуга План на тему: “Мои жизненные планы и профессиональная карьера”
План на тему: “Мои жизненные планы и профессиональная карьера” Использование техники объемной лепки в изготовлении традиционной игрушки из ваты
Использование техники объемной лепки в изготовлении традиционной игрушки из ваты Открытый урок
Открытый урок Объект, предмет, задачи педагогики
Объект, предмет, задачи педагогики Тестирование Google Forms
Тестирование Google Forms Диагностический материал для исследования пространственных представлений старших дощкольников
Диагностический материал для исследования пространственных представлений старших дощкольников Творческий проект. Картинная галерея комнаты школьника Искорка
Творческий проект. Картинная галерея комнаты школьника Искорка Учитель для одаренных детей
Учитель для одаренных детей Профессия продавец
Профессия продавец Мастер-класс Золотые Ручки. Одуванчики
Мастер-класс Золотые Ручки. Одуванчики Оздоровление дошкольников в непосредственно- образовательной деятельности используя ИКТ
Оздоровление дошкольников в непосредственно- образовательной деятельности используя ИКТ