Задача. Найдите расстояние от точки пересечения медиан прямоугольного треугольника до его катета, равного 12, если гипотенуза ра

Задача. Найдите расстояние от точки пересечения медиан прямоугольного треугольника до его катета, равного 12, если гипотенуза равна 15.
Что требуется найти в задаче?
Расстояние от точки пересечения медиан до катета, равного 12, т.е. ОН.
Что мы сразу можем найти по данным задачи?
Из теоремы Пифагора второй катет.
Что мы знаем о точке пересечения медиан треугольника?
Медианы пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, начиная от вершины.
Из какой фигуры мы можем найти искомое расстояние?
Из прямоугольного треугольника ОНL.
Как данная фигура связана с другими фигурами?
Треугольник ОНL подобен треугольнику АСL.
А
?
9
2к
1к
Что следует из подобия треугольников?
Равенство отношений соответствующих сторон.
Отношение каких сторон мы возьмём?
LО : LА = ОН : АС
Чему равно отношение LО : LА?
LО : LА = 1/3.
Составим план решения задачи.
1.Находим катет АС.
2.Рассматриваем подобные треугольники: ∆ ОНL и ∆ АСL.

Дано: АВС – прямоугольный треугольник,
АВ=15, ВС=12,
АК=ВК, СL=ВL.
Найти: ОН.
Решение.
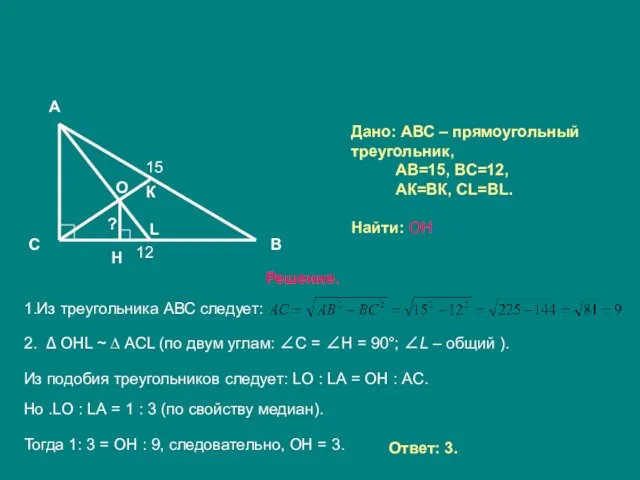
1.Из треугольника АВС следует:
2. ∆ ОНL ~ ∆ АСL (по двум углам: ∠С = ∠Н = 90°; ∠L – общий ).
Из подобия треугольников следует: LО : LА = ОН : АС.
Но .LО : LА = 1 : 3 (по свойству медиан).
Тогда 1: 3 = ОН : 9, следовательно, ОН = 3.
Ответ: 3.