Актуальность темы

Основополагающий вопрос:
Можно ли жить без знаний
процентов в современном мире?

Проблемные вопросы:
Что такое процент?
Что надо знать о процентах?
Практическое применение темы.
Что значит жить на проценты?
Какие задачи на проценты решают учащиеся на уроках?
Темы исследований учащихся:
Приходится ли решать задачи на проценты людям разных профессий.
Проценты и банковские расчеты.
Встречаются ли проценты в периодической печати и что они обозначают?
Установить связь между точными и естественными науками с помощью темы «Проценты».

Задачи проекта
Научить решать задачи на проценты.
Сформировать понимание часто встречающихся оборотов речи со словом «процент».
Показать связь содержания занятий с жизнью и другими предметами.

Цели проекта:
Формирование у школьников представлений о математике как общекультурной ценности.
Демонстрация использования математических знаний в различных сферах деятельности человека.
Приобщить к творческой деятельности.
Выработать умение мыслить.
Формировать компетентность в социально- бытовой сфере.
Воспитывать трудолюбие.
Развивать самостоятельность.

Брать ссуду в банке или купить в кредит?
Может быть выгоднее накопить денег для покупки дорогостоящей вещи?
Чтобы ответить на эти вопросы, требуется умение решать задачи по теме «Проценты».
Вы умеете рационально тратить деньги?
Вы можете купить товар, на приобретение которого у вас недостаточно средств?
Вы знаете, какие для этого существуют возможности?
А может быть вы будущий бизнесмен, экономист, банковский работник или химик?
Тогда вам просто необходимо
«дружить с процентами».

Проценты – одно из математических понятий, которые часто встречаются в повседневной жизни.
Понимание процентов и умение производить процентные расчеты в настоящее время необходимо каждому человеку, это способствует «вхождению» в современную информационно-экономическую среду.

"Ключевые" задачи на проценты
Нахождение процента
от числа
Нахождение числа по
его проценту
Нахождение процентного
отношения двух чисел

Основные типы задач на проценты
В простейших задачах на проценты некоторые величина а принимается за 100%, а ее часть b выражается p %.
100 % - a
P % - b
100 % - a
P % - b

Нахождение процента
от числа
Чтобы найти процент от числа, надо это число умножить на соответствующую дробь.
20% от 45 кг сахара
равны 45·0,2=9 кг.

Нахождение числа по его проценту
Чтобы найти число по его проценту, надо часть, соответствующую этому проценту, разделить на дробь.
Если 8% от длины бруска составляют 2,4см, то длина всего бруска равна 2,4:0,08=30см

Нахождение процентного отношения двух чисел
Чтобы узнать, сколько процентов одно число составляет от второго, надо первое число разделить на второе и результат умножить на 100%.
9г соли в растворе
массой 180г составляют
9:180·100%= 5%.

Проценты в
банковской
системе

Простой процентный рост
Пусть S - ежемесячная квартплата,
пеня составляет p% квартплаты за каждый день просрочки.
Сумму, которую должен заплатить человек после n дней просрочки обозначим Sn.
Тогда за n дней просрочки пеня составит pn % от S,
а всего придётся заплатить .
Формула простого процентного роста

Сложный процентный рост
Пусть банк начисляет p% годовых, внесенная сумма равна S рублей, а сумма, которая будет через n лет на счете, равна Sn рублей.
Формула сложного процента

Банковский процент
Есть форма вклада под 100% годовых, с правом взять вклад в любое время с получением доли прибыли.
За 1 день вклад увеличится на
За 1 год вклад увеличится на
е = 2,71828 - число Эйлера.

Задача от Олигарха:
Один из наших олигархов положил в коммерческий банк 8 миллионов долларов под 50%. Через год он снял некоторую сумму для покупки яхты, а еще через год на его счету стало 13,5 млн. долларов. Я не спрашиваю, откуда у него такие деньги и где тот банк. Я только хочу знать, почем нынче яхты?
Решение:
1) 8 · 0,5 = 4(млн. долларов) – 50%;
2) 2) 8 + 4 = 12 (млн. долларов) – на счету через год;
3) 3) х млн. долларов – стоимость яхты, тогда после покупки яхты на счету останется (12 – х ) млн. долларов;
4) 4) еще через год на его счету станет
(12 – х) · 0,5 + 12 – х = 13,5;
х = 3.
Ответ: 3 млн. долларов.

Задача бизнесмена:
На сколько процентов необходимо поднять цену товара, чтобы после распродажи его с 20% скидкой доход от продажи составил 5%?
Решение:
Пусть а – первоначальная цена, тогда новое значение цены – b.
b = a · (1-0,01 · 20)·(1+0,01 · р) = 0,8а(1+0,01 · р),
b = а · (1+0,01 · 5) = 1,05а
Составим уравнение:
0,8а · (1+0,01 · р) = 1,05а;
1+0,01р = 1,05 : 0,8;
0,01р = 0,3125;
р = 31,25%
Ответ: цену товара необходимо поднять на 31,25%.

Задача продавца:
Вечером хозяин магазина повысил цену на телевизоры на 30%. За ночь передумал и утром велел снизить цену на 30%. Какой стала цена: прежней? Повысится или понизится?
Решение:
Пусть х грн.– стоимость телевизора, тогда (х+0,3х) грн. – стоимость товара после повышения. Тогда цена утром после повышения составит: (х+0,3) – 0,3(х+0,3х) = 0,91х грн., что меньше, чем х, следовательно цена понизится.
Ответ: понизится

Задача учительницы:
Вчера один депутат с экрана телевизора поведал буквально следующее: «Мы добились повышения зарплаты бюджетникам в 1,5 раза. Это почти 20%». Да зарплату повысили в 1,5 раза, а цены подняли на 50%. Это во сколько раз?
Ответ: в 1,5 раза.

Задачи покупателя:
Цены на все товары повысились на 100%. Как изменилась моя покупательская способность? (Ответ: уменьшилась в два раза.)
Зарплату увеличили в три раза, а цены подняли на 200%. Что стало с моей покупательной способностью? (Ответ: не изменилась.)
Зарплата не изменилась, а все цены снизили на 100%. Что стало с покупательной способностью? Конечно, это шутка. Снизить цену на 100% - это раздавать товар бесплатно.

Задача банкира:
Банк обещает вкладчикам удвоить их сбережения за 5 лет, если они воспользуются вкладом «Накопление» с годовой процентной ставкой 16%. Выполнит ли банк своё обязательство?
Ответ: да, вклад увеличится более чем в два раза.

Задача домохозяйки:
Имеется 150 граммов 70-процентной уксусной кислоты. Сколько воды надо в неё добавить, чтобы получить 5-процентный уксус?
Решение:
1) 150 · 0,7 = 105 грамм кислоты в растворе;
2) 150 - 105 = 45 грамм воды в растворе;
3) 105 : 0,05 = 2100 грамм масса нового раствора;
4) 2100 - 105 = 1995 грамм воды в новом растворе;
5) 1995 - 45 = 1950 грамм нужно добавить воды.
Ответ: 1950 грамм

Задача Бабы-Яги:
Я варю своё волшебное зелье так: к 1,5кг меда она добавила 100гр. растертых волчьих костей, 100гр дёгтя и 300гр слёз кикиморы. Интересно, сколько же процентов варева составляют слёзы кикиморы?
Решение:
1) 1500 + 100 + 100 + 300 = 2000 грамм зелья
2) 300 : 2000 · 100% = 15% зелья составляют слезы кикиморы.
Ответ:15%

Задача про вирусы:
Ужасный вирус пожирает память компьютера очень быстро. За первую секунду он управляется с половиной памяти, за вторую – с одной третьей оставшейся части, за третью секунду – с 25% того, что ещё сохранилось, за четвёртую – с 20% остатка. И тут его настигает антивирус. Какой процент памяти уцелел?
Решение:
1сек. – 50%, 2 сек. - , 3 сек. - , 4 сек. - 5%.
Осталось:
Ответ: 20%

Слово «процент» произошло от латинских слов
pro centum, что буквально означает «за сотню» или «со ста». Проценты дают возможность легко сравнивать между собой части целого, упрощая расчёты.
Пример: Что больше ½ или ¾?
Для чего и когда появился процент?
½ = 50 % < ¾ = 75 %

Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти», так как в Вавилоне пользовались шестидесятеричными дробями. Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы.

Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, в экономических расчетах, в страховании, статистике, науке и технике.
В процентах выражаются ставки налогов, доходность капиталовложений, плата за заемные денежные средства (например, кредиты банка), темпы роста экономики и многое другое.
Римляне брали с должника лихву (т. е. деньги сверх того, что дали в долг). При этом говорили: «На каждые 100 сестерциев долга заплатить 16 сестерциев лихвы».

Процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу) или сотая часть единицы. Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому.
Запись 1% означает 0,01 или 1/100.
Так как 1 % равен сотой части величины,
то вся величина равна 100%
Знакомство с процентом.

В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта.
В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
Pro cento – cento – cto - c/o - %
Как возник знак процента
Изобретение математических знаков и символов значительно облегчило изучение математики и способствовало дальнейшему ее развитию.
Происхождение обозначения.

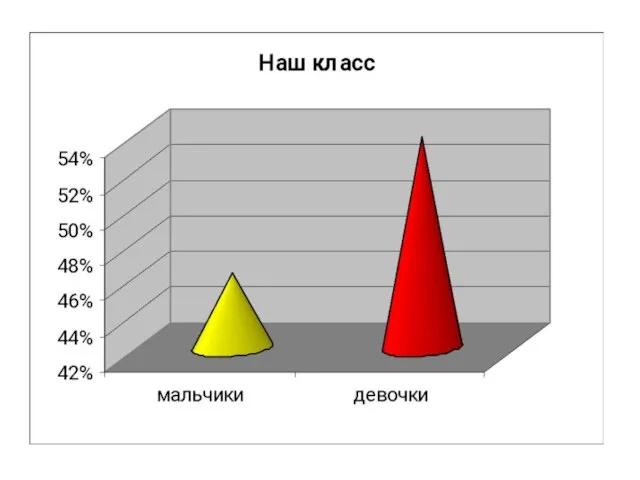
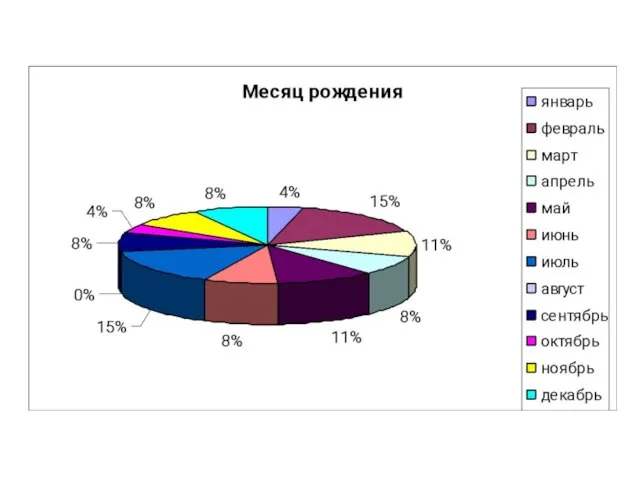
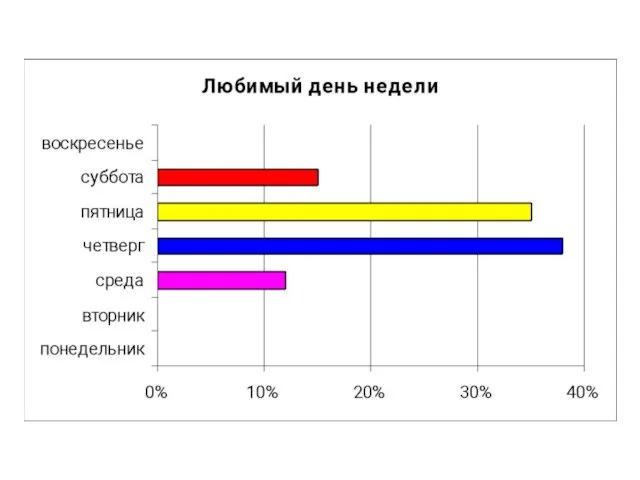
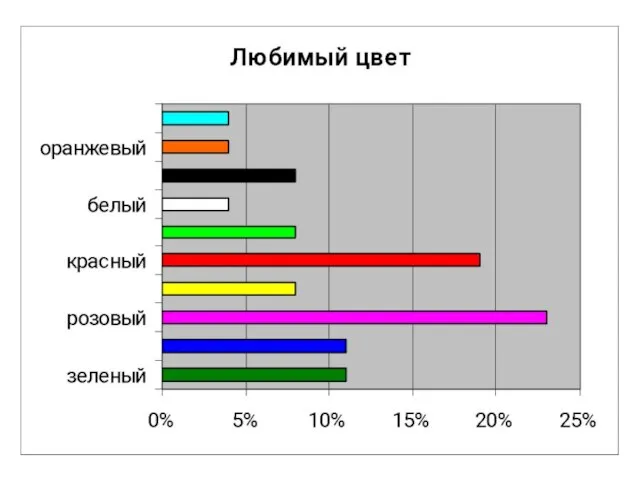
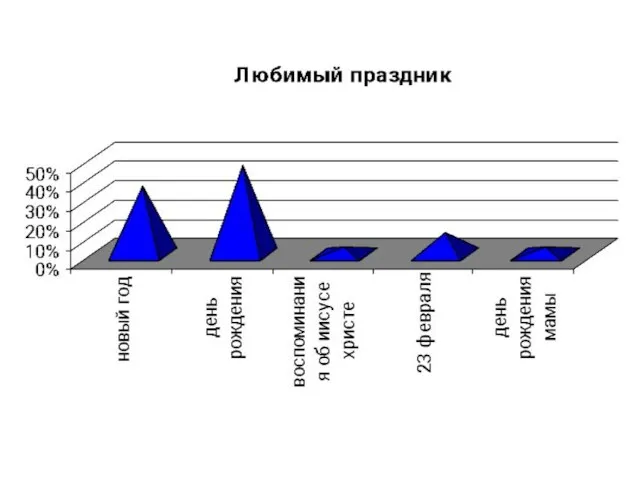
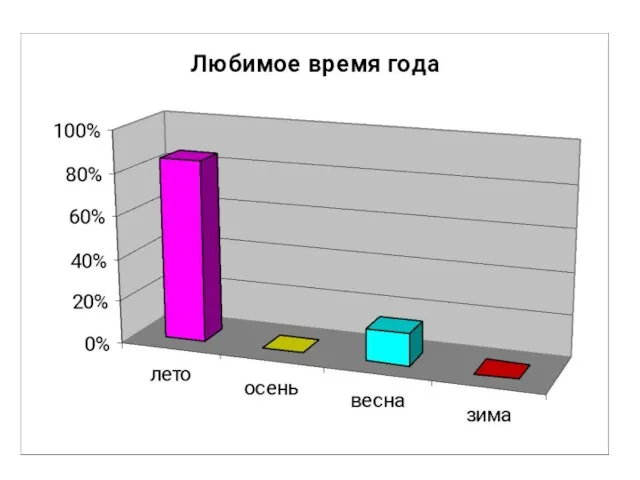
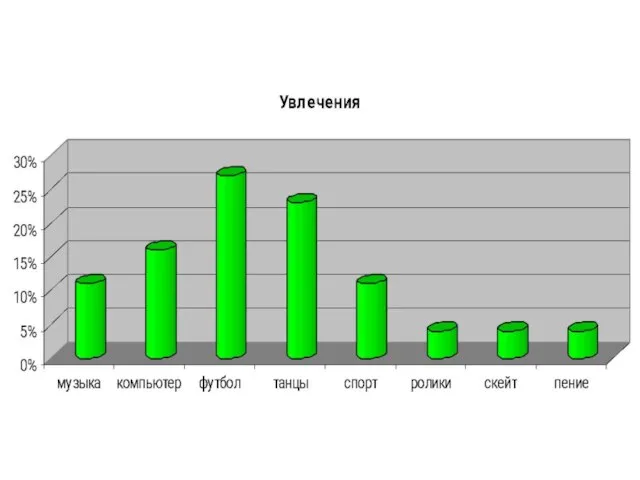
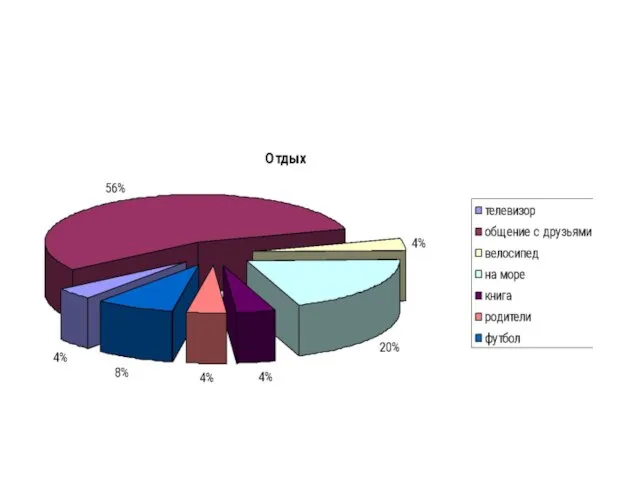
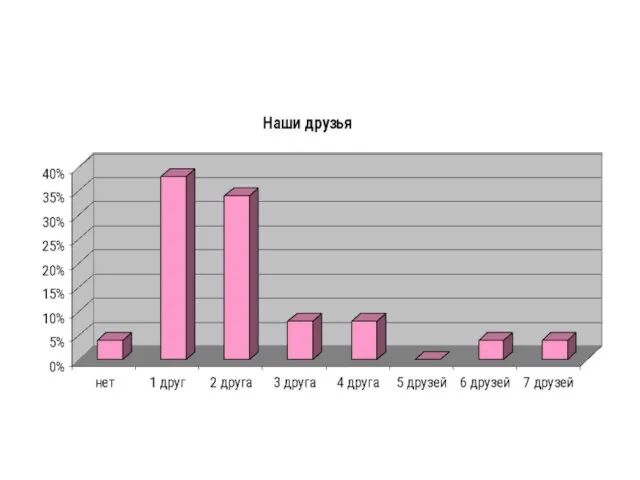
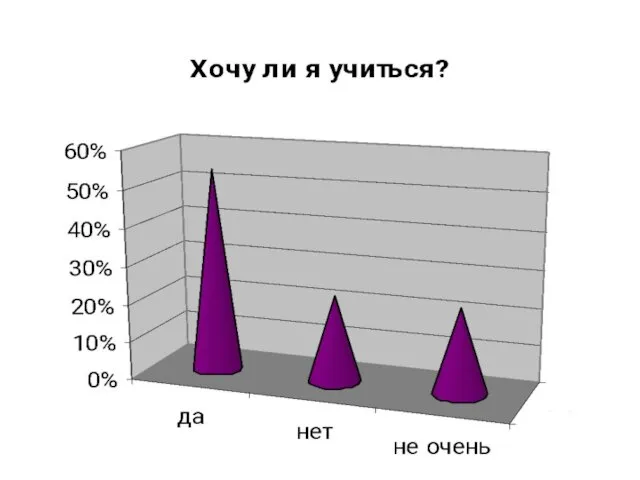
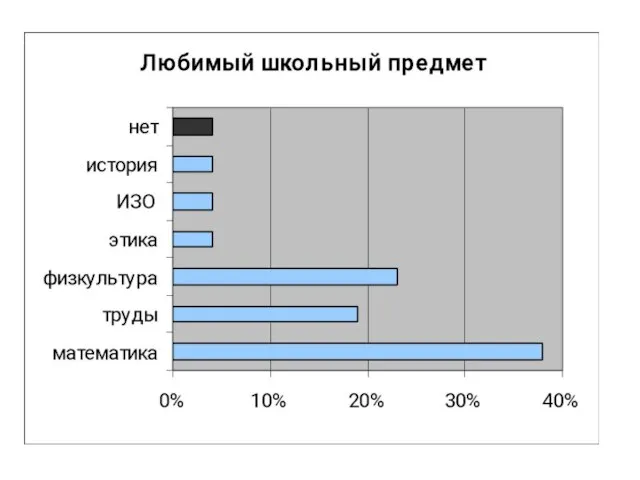
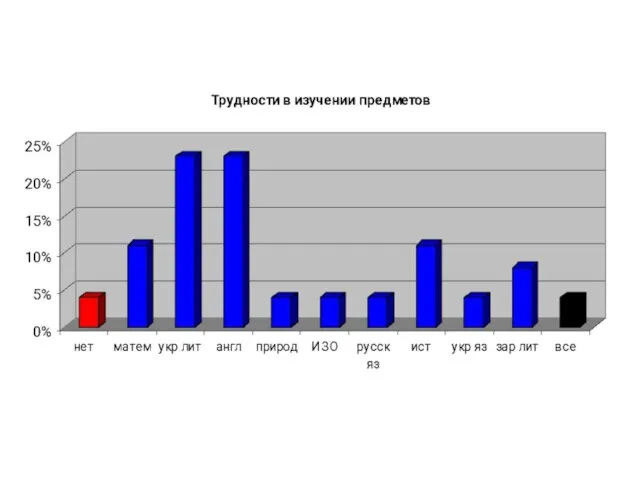
И н т е р е с ы 5-В к л а с с а в п р о ц е н т а х
Наш класс
Месяц рождения.
Любимый день недели.
Любимый цвет.
Любимый праздник.
Любимое время года.
Увлечения.
Отдых.
Наши друзья.
Хочу ли я учиться?
Любимый учебный предмет.
Трудности в изучении предметов.

Проценты в нашей жизни
Темы самостоятельных исследований
Проценты на кухне
Проценты в аптеке
Проценты в банке
Проценты и зарплата
Проценты и выборы

Проценты на кухне
Сколько граммов воды нужно добавить к столовой ложке (25 грамм) 70% уксусной кислоты, чтобы получить 9% уксусную кислоту?

Проценты в аптеке
Условие задачи.
У меня бабушка участница Великой Отечественной Войны. Она пользуется льготами при покупке лекарств. Она меня попросила купить следующие лекарства: анальгин стоимостью – 3,90 грн., кордипин – 4,35 грн., нитроглицерин – 8,92 р.
Ветеранам аптека предоставляет скидку 10%. Сколько денег я сэкономил при покупке лекарств бабушке?

Проценты в банке
Мои родители в прошлом году положили в банк на моё имя 1000 рублей под 20% годовых. Эти деньги мне нужны будут на выпускной вечер. Интересно, какую сумму я получу через 5 лет?

Проценты и зарплата.
Моя мама работает учителем. Она мне рассказала из чего состоит её зарплата и как её начисляют.
Оклад – 1500 гривен
Кл. руководство – 20%
Проверка тетрадей – 10%
Подоходный налог – 15%
Профсоюз – 1% с начисляемой зарплаты
Соц.страх – 0,5% с начисляемой зарплаты
Сумма, не облагаемая налогом – 340 гривен
Зарплата к выдаче - ? гривен

Проценты и выборы
Выборы Президента Украины 7 февраля 2010 г в городе Славянске.
Количество избирателей – 154 340 человек.
Приняли участие в выборах – 76 795 человек.
за Януковича – 68 856 человек
за Тимошенко – 5 291 человек
Против всех – 1 893 человека
Вопрос: сколько процентов избирателей проголосовало за этих кандидатов?

ВОПРОС ДЛЯ РАЗМЫШЛЕНИЯ.
Сколько денег надо вложить в банк, чтобы через 5 лет получить 20000 гривен, если банк платит по срочным вкладам 10% годовых?

В тексте знак процента используется только при числах в цифровой форме, от которых при наборе отделяется неразрывным пробелом (доход 67 %), кроме случаев, когда знак процента используется для сокращённой записи сложных слов, образованных при помощи числительного и прилагательного процентный. Например: 20%-я сметана (означает двадцатипроцентная сметана), 10%-й раствор, 20%-му раствору, но жирность сметаны составляет 20 %, раствор концентрацией 10 % и т. п.Это правило набора введено в действие в 1982 году нормативным документом ГОСТ 8.417—81; ранее нормой было не отделять знак процента пробелом от предшествующей цифры.
В настоящее время правило отбивки знака процента не является общепризнанным. До сих пор многие украинские издательства не следуют рекомендациям ГОСТ 8.417—81 и по-прежнему придерживаются традиционных правил набора, то есть при наборе знак процента от предшествующего числа не отделяется,
что было замечено в школьных учебниках при подготовке данной презентации.
Правила набора.

Ударение в слове процент в единственном и множественном числе во всех падежах сохраняется на втором слоге.
Например: сто один процент; не более восемнадцати процентов.
а) Сочетание «несколько процентов (от чего?) …» используется, если зависимое слово – числительное.
Например, «десять процентов от шестидесяти».
б) Сочетание «несколько процентов (чего?) …» используется, если зависимое слово – существительное, не имеющее количественного значения.
Например, «тридцать процентов населения».

в) Если зависимое слово по смыслу связано с количеством, допустимы обе конструкции.
Например, «шесть процентов зарплаты» и «шесть процентов от зарплаты».
Слова «процент», «проценты» читаются в большинстве случаев в том же падеже, что и числительное.
Например:
1/5 = 20 % - одна пятая равна двадцати (д. п.) процентам (д. п.)
0,6 > 50 % - ноль целых шесть десятых больше пятидесяти (р. п.) процентов (р. п.).
После любого падежа числительных, оканчивающихся словом «тысяча» или «миллион», слово «проценты» ставится в родительном падеже. Например, «прирост производительности труда равен тысяче (д. п.) процентов (д. п.)».

В романе «Господа Головлевы», который написал Михаил Евграфович Салтыков-Щедрин в 19 веке (1875-1880 гг.), описывается, как барыня Арина Петровна Головлева, по словам автора «женщина властная и притом в сильной степени одаренная творчеством», очень быстро рисует себе картину значимости происшедших финансовых изменений. Барыня хорошо владела процентными вычислениями и сразу сознавала серьезность проблемы.
Итак, путешествуем в прошлое: сцены из жизни господ Головлевых из романа М.Е. Салтыкова-Щедрина.
Рассмотрим практическую значимость финансовой математики в литературе.

Однажды бурмистр дальней вотчины, Антон Васильев, окончив барыне Арине Петровне Головлевой доклад о своей поездке в Москву для сбора оброков с проживающих там по паспортам крестьян, вдруг как-то замялся на месте.
Арина Петровна, которая понимала все тайные помыслы своих приближенных людей, немедленно обеспокоилась.
«Что еще?»
- Все-с.
- Не ври! Еще есть! По глазам вижу! Сказывай, какое еще дело за тобой есть? Говори! Не виляй хвостом… сума переметная!
- Есть, действительно…
- Что? Что такое?
- Степан Васильевич дом в Москве продали…
- Ну?
- Продали-с.
- Почему? Как? Не мни! Сказывай!
- За долги… Так нужно полагать! Известно, за хорошие дела продавать не станут.
- Стало быть, полиция продала? Суд?
- Стало быть, что так. Сказываю, в восьми тысячах с аукциона дом пошел.
- Так ты говоришь полиция за 8 тысяч дом-то продала.
- Так точно!
- Это - родительское благословение! Хорош…мерза-вец! За 8 тысяч дом спустил! За 12 покупали!
- За 12 тысяч покупали?
Сколько потеряли! Ступай, потатчик!
Вычислить: Какой убыток в процентах понесла семья Головлевых по вине Степана Васильевича?

Решение:
12000-8000=4000 (рублей).

Иногда применяют и более мелкие доли целого – тысячные, то есть десятые части процента. Их называют «промилле» происходит от лат. «pro mille», что означает в переводе «с тысячи» или «тысячная доля» — 1/10 процента. Обозначается дробью «0 делить на 00» (‰). Как и «процент», тоже используется для обозначения доли чего-либо по отношению к целому.
Соотношение к процентам и десятичным дробям
Знакомьтесь родственник процента – промилле.

Величина в промилле от массы, выраженной в килограммах, эквивалентна массе в граммах. От массы в тоннах — килограммам.
Например, фраза «солёность воды составляет 11 ‰ (одиннадцать промилле)», это то- же самое, что и 1,1 % и означает, что из общей массы воды 0,011 (11 тысячных) занимают соли; так, если взять 1 кг воды, то в ней будет 0,011×1000 = 11 г солей.

Математика нужна!
Математика важна!
В гастрономе как-то дед
Закупался на обед.
Взял он фруктов, колбасы,
Положил всё на весы.
Продавец всё подсчитала,
Старика и обсчитала.
В школе дед учился плохо,
Не заметил он подвоха.
Математику бы знал,
Сохранил бы капитал!
К. Ларин