Содержание
- 2. Лингвистика Байкал 23 августа 2011
- 3. Лингвистика Байкал 23 августа 2011
- 4. Лингвистика Байкал 23 августа 2011
- 5. Анализ данных Байкал 23 августа 2011
- 6. Анализ символьных последовательностей от биоинформатики до лингвистики М.А. Ройтберг Байкал 23 августа 2011 ЦЕЛИ Знакомство с
- 7. Проблематика (молекулярная биология) Медицинские приложения (разработка лекарств, медицинская генетика, персональная медицина) Исследования механизмов функционирования клетки (и
- 9. ДНК: 2 нити; L ~ 105 – 109 нуклеотиды (4)
- 11. An Example: t-RNA From Paul Higgs РНК: 1 нить; L ~ 102 – 103 нуклеотиды (4)
- 12. Белки: 1 нить; L ~ 102 – 103 аминокислоты (20) PDB ID: 2act E.N. Baker, E.J.
- 13. …Gly + Ala… = …GA…
- 14. Данные: последовательности Не только последовательности 1. Пространственные структуры - сравнение, анализ (пример: «докинг») 2. Генные сети
- 15. Основные задачи анализа последовательностей 1. Сравнение - сопоставление в целом (в т.ч. - множественное); определение количественной
- 16. ИСТОРИЯ и ДЛИНЫ tRNA - (1964) - 75 bases (old, slow, complicated method) First complete DNA
- 17. План доклада Выравнивания. Динамическое программирование, графы и алгебра Поиск локальных сходств, затравки Структуры РНК Гиперграфы и
- 18. Тема 1. Выравнивание
- 19. Варианты выравниваний Выровнять две символьные последовательности – удалить из них несколько фрагментов так, чтобы оставшиеся последовательности
- 20. Какой вариант выбрать? А) Б) --ПОДБЕРЕЗОВИК ПОДБЕРЕЗОВИК-- ПРЕДОСИНОВИЧКИ ПРЕДОСИНОВИЧКИ В) Г) Д) ПО-ДБЕРЕЗОВИК-- П-ОДБЕРЕЗОВИК-- ПО-ДБЕРЕЗОВИ-К- ПРЕДОСИН-ОВИЧКИ
- 21. Какой вариант выбрать? Нужно «знать» что-нибудь про эволюцию А) Б) --ПОДБЕРЕЗОВИК ПОДБЕРЕЗОВИК-- ПРЕДОСИНОВИЧКИ ПРЕДОСИНОВИЧКИ В) Г)
- 22. Две одинаковые буквы скорее имеют общего предка, чем две разные буквы Две буквы «одинаковой гласности» скорее
- 23. Две одинаковые буквы скорее имеют общего предка, чем две разные буквы Две буквы «одинаковой гласности» скорее
- 24. Вес выравнивания A T – V V I — - T G S G S M
- 25. Вес выравнивания A T – V V I — - T G S G S M
- 26. ~ L4 - произвольная функция – выпуклая функция ********************************* – линейная f(L) = a + bL
- 27. Эталонные выравнивания
- 28. Структурное и алгоритмическое выравнивания Str) 40 сопоставлений lkCnqli...PPFWKTCPKGKNLCYKmtmraapmvPVKRGCidv riCfnhqssqPQTTKTCSPGESSCYHkqwsdfrgtIIERGCg.. * **************** ****** 1 16 6 AlgSW)
- 29. Str) lkCnqli...PPFWKTCPKGKNLCYKmtmraapmvPVKRGCidv riCfnhqssqPQTTKTCSPGESSCYHkqwsdfrgtIIERGCg.. * **************** ****** 1 16 6 AlgSW) 1 16 6 * **************** ******
- 30. %ID Алгоритм Смита-Уотермана (SW) не может восстановить структурное выр-ние при ID
- 31. Проблемы: 1. Белки( алгоритм Смита-Уотермана): - не работает при слабом сходстве; причина этого не известна; -
- 32. Проблемы 3. Классы штрафных функций: - расширить классы штрафных функций делеций, для которых существуют алгоритмы данной
- 33. Str) lkCnqli...PPFWKTCPKGKNLCYKmtmraapmvPVKRGCidv riCfnhqssqPQTTKTCSPGESSCYHkqwsdfrgtIIERGCg.. ^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ Остров1 Остров 2 Острова – безделеционные фрагменты выравниваний. Вес острова –
- 34. SW выравнивания структурные выравнивания Island score % островов 1. Причины плохого качества выравниваний SW
- 35. Тема 1. Динамическое программирование
- 36. Рекурсия для глобального выравнивания (δ(L)=kL) v, w - слова; a, b – буквы S(v, w) –
- 37. Ориентированный ациклический граф с весами на ребрах Вершина Ребро Ребра направлены и снабжены весами. Путь: ABCE
- 38. Пути (примеры): BEZ = {(BE), (EZ)} (длина 2); вес W(BEZ) = 7 + 5 = 12
- 39. Полные пути – пути из источника в сток (примеры): ADEZ: длина = 3; вес W(ADEZ) =
- 40. ДАНО: Ориентированный ациклический граф с весами на ребрах G = ЗАДАЧА 1 (задача Беллмана) Найти оптимальный
- 41. Пример: предсказание 3D структуры белков (гемоглобин, код белка 1ash, цепь А)
- 43. Дано: последовательность аминокислот Надо: где образуются спирали Дано: последовательность аминокислот Надо: где образуются спирали
- 44. ДАНО: Ориентированный ациклический граф с весами на ребрах G = ЗАДАЧА 1 (задача Беллмана) Найти оптимальный
- 45. Метод динамического программирования (Алгоритм Беллмана, 1953) Проход от стока к источнику: из W есть путь в
- 46. BestW(B) = = min{ W(BC) + BestW(C), W(BD) + BestW(D), W(BE) + BestW(E), }
- 47. BestW(B) = = min{ W(BC) + BestW(C), W(BD) + BestW(D), W(BE) + BestW(E), } Best Weight:
- 48. BestW(A) = = min{ W(AB) + BestW(B), W(AC) + BestW(C), W(AD) + BestW(D), } Для любой
- 49. ВРЕМЯ РАБОТЫ ~ к-во РЕБЕР ПАМЯТЬ ~ к-во ВЕРШИН
- 50. 1.2. Алгебраическая основа алгоритма Беллмана 1. Динамическое программирование, графы и алгебра
- 51. Задача-подсказка S = = a1 ⋅ b1 + a1 ⋅ b2 + ... + a1 ⋅
- 52. Решение S = a1 ⋅ (b1 + b2 + ... + b1000 ) + + a2
- 53. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение Умножение
- 54. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение Умножение
- 55. Мультипликативные веса путей BEZ = {(BE), (EZ)} (длина 2); вес W(BEZ) = 7 + 5 =
- 56. ДАНО: Ориентированный ациклический граф с весами на ребрах G = ЗАДАЧА 2 («задача Больцмана») Найти сумму
- 57. Лю́двиг Больцман (Ludwig Eduard Boltzmann, 1844 – 1906; Австро-Венгрия, Италия), основатель статистической меха-ники и молекулярно-кинетической теории
- 58. Интерпретации: 1. Вероятность прохода лабиринта: Вершины – города; Ребра - дороги; Вес ребра: вероятность перехода по
- 59. Проход от стока к источнику: из W есть путь в V => => W обрабатывается позже,
- 60. Проход от стока к источнику: из W есть путь в V => => W обрабатывается позже,
- 61. Проход от стока к источнику: из W есть путь в V => => W обрабатывается позже,
- 62. Проход от стока к источнику: из W есть путь в V => => W обрабатывается позже,
- 63. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение Умножение
- 64. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение Умножение
- 65. Sum(B) = = M(BCEZ) + M(BCFZ) + M(BDZ) + M(BDEZ) + M(BEZ) = = W(BC)*M(CEZ) +
- 66. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение Умножение
- 67. Sum(B) = = M(BCEZ) + M(BCFZ) + M(BDZ) + M(BDEZ) + M(BEZ) = = W(BC)*M(CEZ) +
- 68. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение Умножение
- 69. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение Умножение
- 70. Сочетательный закон (ассоциативность): Сложение Умножение (a+b)+c = a+(b+c) (a*b)*c = a*(b*c) Переместительный закон (коммутативность): Сложение a+b
- 71. Полукольцо A – это множество, на котором заданы две бинарные всюду определенные операции + и *
- 72. Примеры полуколец. Первая операция – аналог сложения («целевая операция»), вторая – аналог умножения («соединяющая операция»): на
- 73. ДАНО: Ориентированный ациклический граф с весами на ребрах G = ЗАДАЧА 1 Найти оптимальный полный путь,
- 74. Метод динамического программирования (Алгоритм Беллмана) Проход от стока к источнику: из W есть путь в V
- 75. ДАНО: Ориентированный ациклический граф с весами на ребрах G = ; веса W(e) – элементы полукольца
- 76. ВРЕМЯ РАБОТЫ ~ к-во РЕБЕР ПАМЯТЬ ~ к-во ВЕРШИН ДАНО: Ориентированный ациклический граф с весами на
- 77. Замечание 1. Память ВРЕМЯ РАБОТЫ ~ к-во РЕБЕР ПАМЯТЬ ~ к-во ВЕРШИН ПАМЯТЬ МОЖЕТ БЫТЬ МЕНЬШЕ
- 78. Замечание 2. Различие между min и суммой: argmin Рекуррентное уравнение (минимальный путь) BestW(V) = min{ W(VB)
- 79. Раздел 3 Гиперграфы: знакомство Пока без слайдов ☹ Развернутый план 1. Задача о триангуляции выпуклого треугольника.
- 80. 3.1. Задача о триангуляции (рисунок на доске) Идея сведения: провести диагональ, разбить на два многоугольника меньшего
- 81. Задача о триангуляции (рисунок на доске) Идея сведения: провести диагональ, разбить на два многоугольника меньшего размера
- 82. Задача о триангуляции (рисунок на доске) Дан выпуклый многоугольник. Каждой диагонали приписан вес – положительное число.
- 83. �3.2. Понятие гиперграфа Определение 1. Граф G – это пара , где V – это множество
- 84. �3.2. Понятие гиперграфа Определение 3. Путь в графе G= – это простая цепь, узлы которой помечены
- 85. Гиперпуть
- 86. An Example: t-RNA From Paul Higgs Вторичная структура РНК.
- 87. 3. Выравнивание последовательностей РНК с заданной вторичной структурой.
- 88. Пример: РНК и гиперпуть
- 89. Тема 4. Поиск локальных сходств Использование затравок (seed) Избирательность и чувствительность Типы затравок (seed model)
- 90. Затравки: фильтрация пространства поиска Сначала ищем небольшие и легко диагностируемые участки сходства («затравочные сходства», seed similarities).
- 91. «Классическая затравка» (пример: 6 совпадений подряд) Точные совпадения : Затравка («затравочное слово», описание затравочных сходств) :
- 92. Затравка ловит сходство (затавка соответствует сходству) Затравка ##### ? seed Затравочное сходство (… выравнивание) ATGCAA ATGCAA
- 93. Недостатки подхода Случайное сходство Пропущенное сходство: не содержит затравок ###### ATCAGTGCAATGCTCATGAA ::|::::||||||:::..:: CCCGACACAATGCGTGACCC ##☹### [16 of
- 94. Две проблемы “Избирательность” Затравка может НЕ быть частью важного (для нас) сходства “Чувствительность” Важное (для нас)
- 95. Что может быть мерой избирательности и чувствительности Избирательность затравки: ~ 4-weight вероятность ее обнаружения при сравнении
- 96. Множество важных [целевых] выравниваний и их вероятности Выравнивания фиксированной длины без удалений L=18 Вероятностная модель: Бернулли
- 97. Разреженные затравки Ma, Tromp, Li 2002 (PatternHunter) Затравка: ###--#-## ‘#’ : должно быть совпадение ‘-’ :
- 98. Разреженные затравки: в чем преимущество? For spaced seeds, hits at subsequent positions are “more independent events”
- 99. Sensitivity: PH weight 11 seed vs BLAST 11 & 10 [after Ma, Tromp and Li]
- 100. single filter based on several distinct seed patterns each seed pattern detects a part of interesting
- 101. Пример: ВСЕ (18,3) Обнаружить все сходства длины 18, в которых не более 3 несовпадений Чувствительность =
- 102. Пример: ВСЕ (18,3) Обнаружить все сходства длины 18, в которых не более 3 несовпадений Множественная затравка
- 103. Пример: ВСЕ (18.3) ###-##---#-### ###---#--##-# ###---#--##-# w=7 w=9
- 104. #### ###-## Пример: ВСЕ (18.3). Избирательности w=4 ~39. 10-4 w=5 ~9.8 10-4 w=7 ~1.2 10-4 w=9
- 105. СПАСИБО за ВНИМАНИЕ 0. Введение 1. Выравнивания 2. ДП и алгебра 3. Гипернрафы и РНК 4.
- 106. Инициальный (гипер) путь Терминальный (гипер) путь Полный (гипер) путь
- 107. Вес гиперпути ДОПИСАТЬ !!! М-ВЕС НАД ПОЛУКОЛЬЦОМ
- 108. 3.3. Задача Больцмана для гиперграфов. . Формулировка задачи Больцмана. .
- 109. �Подход к решению Терминальная сумма Больцмана вершины V: F(V) – множество всех терминальных гиперпутей с начальной
- 110. �Терминальные суммы Больцмана для гиперребер Терминальная сумма Больцмана гиперребра y: FF(y) – множество всех терминальных гиперпутей
- 111. �Терминальные суммы Больцмана для гиперребер: рекурсия Утверждение. Пусть y = - гиперребро. Тогда S(y) = W(y)*Sum(W1)*…*
- 112. �Терминальные суммы Больцмана для гиперребер: рекурсия 2) существует взаимно-однозначное соответствие между дере-вьями T ∈ Fr(y) и
- 114. Скачать презентацию






























































































![Множество важных [целевых] выравниваний и их вероятности Выравнивания фиксированной длины без удалений](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464853/slide-95.jpg)


![Sensitivity: PH weight 11 seed vs BLAST 11 & 10 [after Ma, Tromp and Li]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464853/slide-98.jpg)













 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут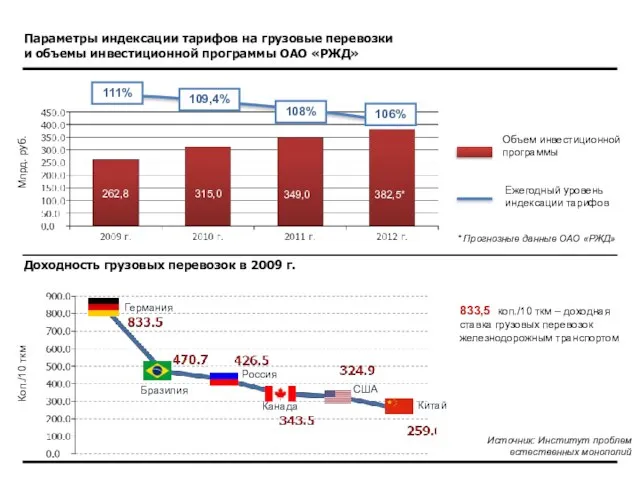 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе