Бортовые радиолокационные комплексы

Согласованный фильтр
Согласованный фильтр — линейный оптимальный фильтр, позволяющий получить максимальное отношение сигнал/шум на выходе фильтра для сигналов известной формы.
Линейный фильтр вносит линейные искажения. Если на нелинейное устройство подать моногармонический сигнал (обычную синусоиду) с одной частотой, то на выходе устройства, посмотрев на спектр, увидим новые спектральные составляющие, гармоники. У линейного устройства новые спектральные составляющие не появляются. На выходе любого линейного устройства, те же самые спектральные составляющие, что и на его входе, без добавления новых гармоник, у этих устройств изменяются только амплитуда и фаза.
Оптимальный фильтр, оптимальный это значит, что он достигает какого-то наилучшего качества. Если мы говорим про оптимальность, то мы должны говорить и про критерий оптимальности, т.е. что у нас достигается наилучшим способом. В данном случае критерием оптимальности является отношение сигнал/шум.

Для каждого сигнала существует свой согласованный фильтр. Сигнал на выходе любого линейного фильтра, в том числе и согласованного, определяется выражением:

Свойства согласованного фильтра
Для любого линейного фильтра сигнал на выходе определяется через свертку сигнала на входе и его импульсной характеристики.
Импульсная характеристика фильтра это реакция фильтра (т.е. то что мы получим на выходе фильтра), на дельта импульс.
Если на вход фильтра подадим дельта импульс, то на выходе получим отклик, этот отклик и есть импульсная характеристика. Дельта импульс это математическая абстракция, это импульс, который имеет бесконечно большую амплитуду, бесконечно малую длительность и площадь этого импульса равна единице. На практике, такой дельта импульс можно заменить коротким импульсом. Спектр дельта импульса равномерен и бесконечен.

Импульсная характеристика согласованного фильтра
Импульсная характеристика СФ имеет отзеркаленную форму сигнала, для которого фильтр согласован:
где Ts – длительность сигнала;
s – сигнал;
k – константа, сигнал можно умножать на любую константу.
В формуле t со знаком минус, сигнал отзеркалили по времени.
Не важно какую амплитуду имеет сигнал, если по форме сигнал повторяет импульсную характеристику, то фильтр будет согласован для этого сигнала. На картинке ниже представлено два примера. Есть треугольный сигнал, осциллограмма в виде треугольного импульса.

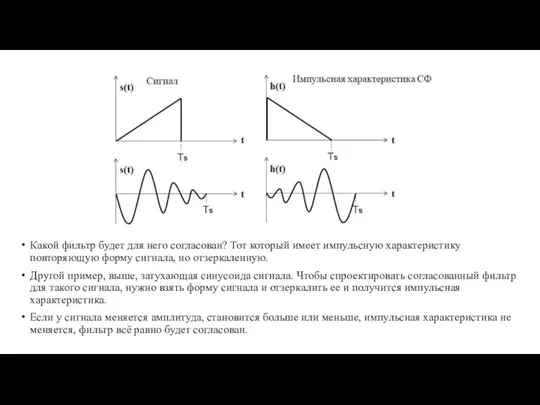
Какой фильтр будет для него согласован? Тот который имеет импульсную характеристику повторяющую форму сигнала, но отзеркаленную.
Другой пример, выше, затухающая синусоида сигнала. Чтобы спроектировать согласованный фильтр для такого сигнала, нужно взять форму сигнала и отзеркалить ее и получится импульсная характеристика.
Если у сигнала меняется амплитуда, становится больше или меньше, импульсная характеристика не меняется, фильтр всё равно будет согласован.

Частотные характеристики согласованного фильтра
Комплексная частотная передаточная характеристика СФ комплексно сопряжена с Фурье-образом сигнала:
где H(f) – частотная передаточная характеристика фильтра;
S(f) – Фурье-образ сигнала;
T – длительность сигнала;
k – константа.
Комплексная экспонента е-i2πTf говорит о сдвиге фаз, возникшем в результате задержки сигнала в фильтре на время T. Откуда взялась комплексная экспонента? Любой фильтр вносит задержку, а комплексная экспонента поворачивает фазу сигнала.
Эта функция H(f) комплексная, у нее есть мнимая и реальная части. Формула с точностью до постоянного множителя (константы) повторяет Фурье-образ сигнала S(f). Единственное, нужно взять Фурье-образ и сделать над ним комплексное сопряжение. Фурье-образ сигнала это результат преобразования Фурье. Это комплексный спектр сигнала.
Комплексная частотная передаточная характеристика СФ комплексно сопряжена с Фурье-образом сигнала с точностью до какого-то постоянного коэффициента. Импульсная характеристика повторяет форму сигнала, частотная характеристика повторяет спектр сигнала, только комплексно сопряжена.
Комплексное сопряжение. Если есть комплексное число в котором есть реальная и мнимая часть, то комплексное число сопряженное, это число у которого меняется знак мнимой части: c=a+jb и c=a-jb.

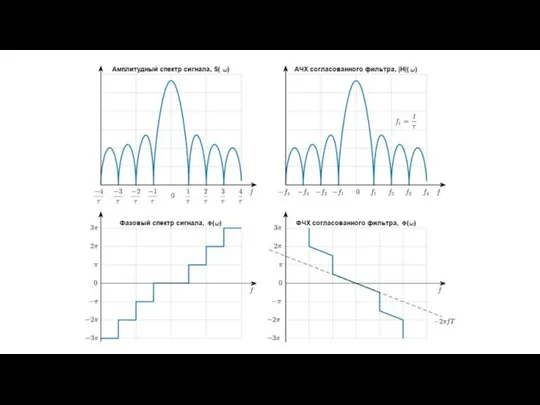
АЧХ и ФЧХ согласованного фильтра
Из передаточной характеристики H(f) получаем АЧХ и ФЧХ. Чтобы получить АЧХ нужно у этой функции взять модуль. АЧХ согласованного фильтра с точностью до постоянного коэффициента k повторяет амплитудный спектр сигнала:
ФЧХ согласованного фильтра повторяет фазовый спектр сигнала с обратным знаком и с учетом задержки:
где ψs(f) — фазовый спектр сигнала.

Отклик согласованного фильтра
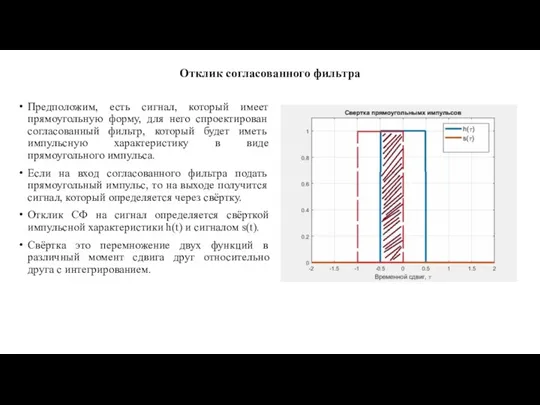
Предположим, есть сигнал, который имеет прямоугольную форму, для него спроектирован согласованный фильтр, который будет иметь импульсную характеристику в виде прямоугольного импульса.
Если на вход согласованного фильтра подать прямоугольный импульс, то на выходе получится сигнал, который определяется через свёртку.
Отклик СФ на сигнал определяется свёрткой импульсной характеристики h(t) и сигналом s(t).
Свёртка это перемножение двух функций в различный момент сдвига друг относительно друга с интегрированием.

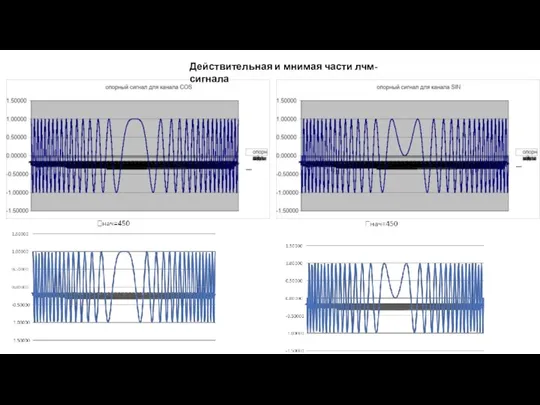
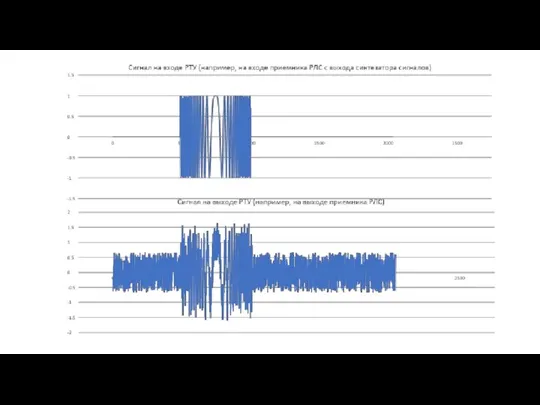
Действительная и мнимая части лчм-сигнала