Демонстрационный вариант 2009г.

Часть 1
№ 1
Расположите в порядке возрастания числа:
0,0902; 0,09; 0,209.
1) 0,209; 0,0902; 0,09
2) 0,09; 0,0902; 0,209
3) 0,09; 0,209; 0,0902
4) 0,0902; 0,09; 0,209

Часть 1
№ 2
Какое из чисел √0,004, √4000, √400 является
рациональным?
1) √0,004
2) √4000
3) √400
4) ни одно из этих чисел

Часть 1
№ 3
Дневная норма потребления витамина С
составляет 60 мг. Один мандарин в среднем
содержит 35 мг витамина С.
Сколько примерно процентов дневной
нормы витамина С получил человек,
съевший один мандарин?
1) 170% 2) 58% 3) 17% 4) 0,58%

Часть 1
№ 4
Найдите значение выражения
при а = 8,4; b = –1,2; с = – 4,5.
Ответ: __________________
а + b
с
– 1,6

Часть 1
№ 5
Цена килограмма орехов a рублей. Сколько
рублей надо заплатить за 300 граммов этих
орехов?
1) 300 (р.)
2) 300a (р.)
3) 0,3a(р.)
4) 10a (р.)
a
3

Часть 1
№ 6
В каком случае выражение преобразовано в
тождественно равное?
1) 3(x−y) = 3x−y 2) (3+x)(x−3) = 9−x2
3) (x−y)2 = x2−y2 4) (x+3)2 = x2+6x+9

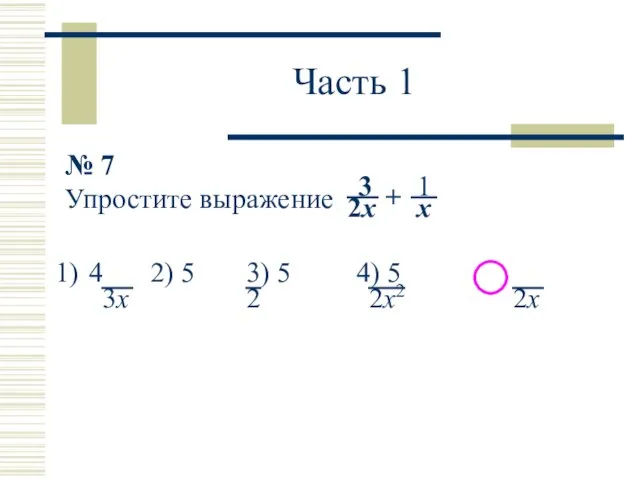
Часть 1
№ 7
Упростите выражение
4 2) 5 3) 5 4) 5
1
3
x
+
2x
2x2
2
2x
3x

Часть 1
№ 8
Найдите частное
Ответ запишите в виде десятичной дроби.
Ответ: ______________________
2,4 ·10- 5
2 ·10- 3
0,012

Часть 1
№ 9
Решите уравнение 3 – 2х = 6 – 4(х + 2).
Ответ: ______________________
Решение

Часть 1
№ 10
Прямая y = 2x пересекает параболу
y = – x2 + 8 в двух точках. Вычислите
координаты точки А.
Ответ: ______________________
Решение

Часть 1
№ 11
Путь от поселка до железнодорожной станции
пешеход прошел за 4 ч, а велосипедист проехал
За 1,5 ч. Скорость велосипедиста на 8 км/ч
больше скорости пешехода. С какой скоростью
ехал велосипедист?
Какое уравнение соответствует условию
задачи, если буквой х обозначена скорость
велосипедиста (в км/ч)?

Часть 1
№ 12
Решите неравенство 10x − 4(2x − 3) > 4.
1) х > – – 2) x > 8 3) x > – 4 4) x < – 4
4
1
Решение

Часть 1
№ 13.
На рисунке изображен график функции
y = x2 + 2x. Используя график, решите
неравенство x2 + 2x > 0.
1) (−∞;0) 2) (−∞;−2)∪(0;+∞)
3) (–2; 0) 4) (−2;+∞)

Часть 1
№ 14
Каждой последовательности, заданной формулой n-го члена (левый столбец), поставьте в соответствие верное утверждение (правый столбец).
А) xn = n2 1) Последовательность – арифметическая прогрессия
Б) yn = 2n 2) Последовательность – геометрическая прогрессия
В) zn = 2n 3) Последовательность не является прогрессией
Ответ:

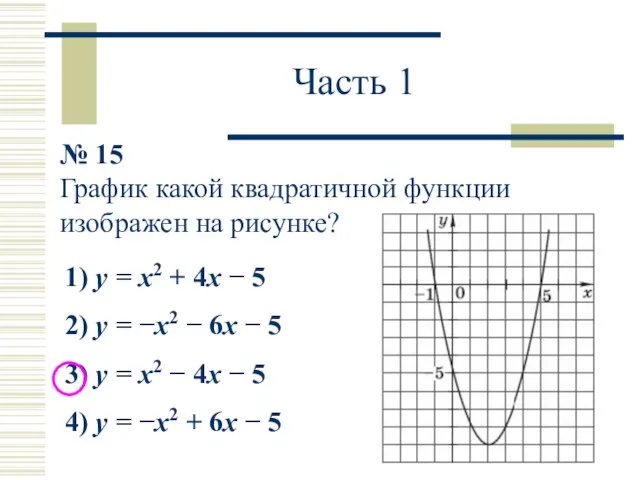
Часть 1
№ 15
График какой квадратичной функции
изображен на рисунке?
1) y = x2 + 4x − 5
2) y = −x2 − 6x − 5
3) y = x2 − 4x − 5
4) y = −x2 + 6x − 5

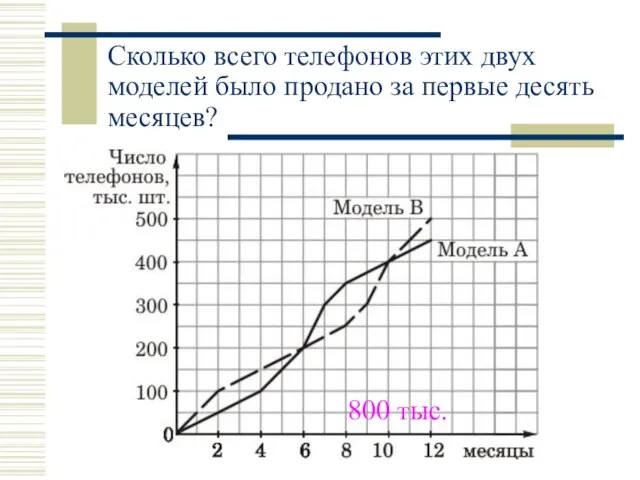
Часть 1
№ 16
Фирма начала продавать две новые модели
телефонов — А и В. На графиках показано,
как росло в течение года количество
проданных телефонов. (По горизонтальной
оси откладывается время, прошедшее с
начала продаж, в месяцах; по вертикальной
— число телефонов, проданных с начала
продаж, в тыс. шт.). Сколько всего
телефонов этих двух моделей было продано
за первые десять месяцев?

Сколько всего телефонов этих двух моделей было продано за первые десять месяцев?
800 тыс.

Часть 2
№ 17. Постройте график функции
Укажите наименьшее значение
этой функции.
Решение

Часть 2
№ 18
Выясните, имеет ли корни уравнение
х2 + 2х√5 + 2х = – 11
Решение

Часть 2
№ 19
Найдите сумму всех натуральных чисел, не
превосходящих 160, которые не делятся на 4.
Решение

Часть 2
№ 20
Найдите наименьшее значение выражения
(2х + у + 3)2 + (3х – 2у + 8)2
и значения х и у, при которых оно
достигается.
Решение

Часть 2
№ 21
Найдите все значения k, при которых
прямая y = kx пересекает в трех различных
точках ломаную, заданную условием:
2х + 4, если x < – 3
y = – 2, если – 3 ≤ x ≤ 3
2x – 8, если х > 3.
Решение

Формулы сокращенного умножения

Решение
3 – 2х = 6 – 4(х + 2)
3 – 2х = 6 – 4х – 8
– 2х + 4х = 6 – 8 – 3
2х = – 5
х = – 2,5
Ответ: – 2,5

Решение:
2x = – x2 + 8
x2 + 2x – 8 = 0
По теореме Виета:
Если x = 2, то у = 2 ⋅ 2 = 4

Решение
10x − 4(2x − 3) > 4
10х – 8х + 12 > 4
2х > 4 – 12
2х > – 8
х > – 4

Решение:
Графиком функции
является парабола, ветви которой направлены вверх, т. к. а > 0.
M(x0, y0) – вершина параболы:
х0 = – 4 , у0 = 8 – 16 + 5 = – 3
Прямая х = – 4 ось симметрии параболы.
Нули функции:
Дополнительные точки:
Справочный материал

Решение
х2 + 2х√5 + 2х = – 11
Представим уравнение в виде
х2 + 2(√5 + 1)х + 11 = 0
Определим знак дискриминанта:
D1 = (√5 + 1)2 – 11 = 5 + 2√5 + 1 – 11 = 2√5 – 5
Так как 2√5 – 5 = √20 – √25 < 0, то
уравнение корней не имеет.
Ответ: не имеет.

Решение
Пусть S - искомая сумма; S = S1 − S2, где S1 - сумма всех натуральных чисел, не превосходящих 160, S2 - сумма всех
натуральных чисел, кратных 4 и не превосходящих 160.
S1
В последовательности (ап) чисел, кратных 4 и не
превосходящих 160, а1 = 4, ап = 160. Найдем число членов этой последовательности. Так как она задается формулой
ап = 4п, то 4п = 160, п = 40.
S2
S = 161 · 80 – 82 · 40 = 40(322 – 82) = 40 · 240 = 9600

Решение
Значение, равное 0, достигается только в том случае, когда 2x + y + 3 и 3x – 2y + 8 равны нулю одновременно.
Составим систему уравнений 2x + y + 3 = 0
3x – 2y + 8 = 0.
Решив её, получим: х = – 2, у = 1.
Таким образом, наименьшее значение выражения равно 0, оно достигается при х = – 2, у = 1.
Ответ: наименьшее значение выражения равно 0, оно достигается при х = – 2, у = 1.