Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений

Содержание
Дискретизация
Частотная область
Гребенчатый фильтр
Теорема Найквиста-Котельникова
Дискретизация аналогового сигнала
Ряд Котельникова и Ряд Уиттакера
Теорема (Найквиста-Котельникова)
Алиасинг
Префильтрация
Алгоритм растеризации Гупты-Спрулла

Дискретизация
Этот раздел посвящен проблемам представления непрерывного двумерного цветового сигнала, которым является изображение, на дискретной растровой сетке.
Процесс получения дискретной аппроксимации непрерывного сигнала называется дискретизацией(англ. sampling).
Изображение в компьютере хранится в дискретном виде.
Для получения такого дискретного представления из непрерывных аналоговых изображений реального мира (как мы их видим глазами или через оптические устройства) и применяется дискретизация.
Дисплей фактически осуществляет реконструкцию аналогового изображения по его дискретизированному представлению.

Обработка сигналов
Наиболее корректно рассматривать возникающие проблемы в рамках теории обработки сигналов (англ. signal processing).
Двумерное изображение можно представлять как двумерный сигнал, рассматривая его как отображение
, где C - атрибут изображения, - интенсивность ( C - отрезок) или цвет; в последнем случае чаще всего C - RGB-куб
В аналоговой форме этот сигнал непрерывный (определенный на прямоугольнике D ), а в дискретной - определенный лишь на точках растра D
Теория обработки сигналов рассматривает периодические сигналы, определенные на всем континууме .
Поэтому для рассмотрения изображений, определенных на прямоугольнике, поступают двояко: либо трактуют как сигнал, равный 0 везде кроме данного прямоугольника, либо считают длину и ширину периодами и производят "замощение" всей плоскости сдвинутыми на периоды копиями изображения.

Частотная область
Сигналы рассматривают как в пространственной области (англ. spatial domain) - это обычная область определения , так и в частотной области (англ. frequency domain), которая получается как область определения коэффициентов разложения сигнала по тригонометрической системе Фурье.
Частотная область представляет из себя .
Частотное представление F(f) для одномерной функции I(x) рассчитывается при помощи преобразования Фурье

Гребенчатый фильтр
Обычно дискретизация происходит путем измерения сигнала (взятия значения функции) через равные промежутки в области определения. Эта операция математически описывается как умножение функции I(x) на гребенчатый фильтр, состоящий из последовательности равномерно сдвинутых функций Дирака :
где T = 1/fs - период, а fs - частота дискретизации Интересным свойством функции Comb является то, что ее преобразование Фурье также есть функция Comb, но с другими амплитудой (не 1, а fs ) и частотой (также fs ).

Теорема Найквиста-Котельникова
Теорема Найквиста-Котельникова дает ответ на вопрос, какой частоты дискретизации fs достаточно для того, чтобы не произошло потери информации, т.е. чтобы по дискретизованному сигналу можно было восстановить исходный.
Применительно к изображениям "Какая разрешающая способность должна быть у растра, чтобы он сохранил все детали исходного аналогового изображения".
Хотя потеря информации даже в случае соблюдения условий теоремы Котельникова произойдет из-за того, что значения дискретизованной функции (растрового изображения) в компьютере сами хранятся с ограниченной точностью.

Дискретизация аналогового сигнала
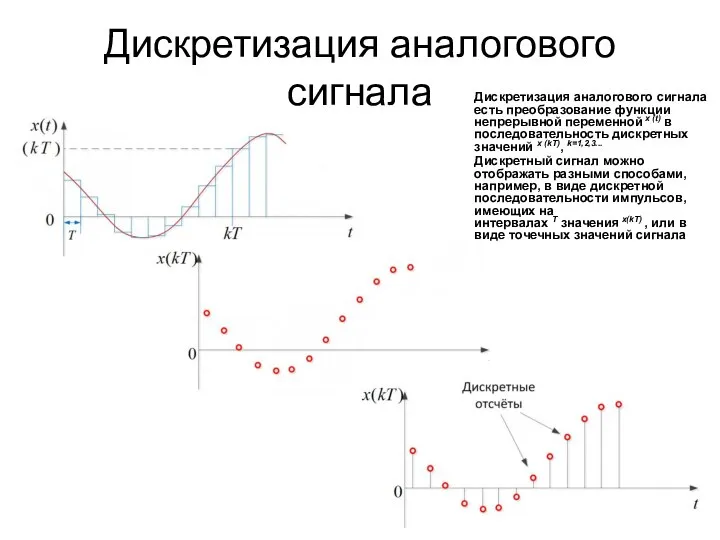
Дискретизация аналогового сигнала есть преобразование функции непрерывной переменной x (t) в последовательность дискретных значений x (kT), k=1,2,3...
Дискретный сигнал можно отображать разными способами, например, в виде дискретной последовательности импульсов, имеющих на интервалах T значения x(kT) , или в виде точечных значений сигнала

Ряд Котельникова
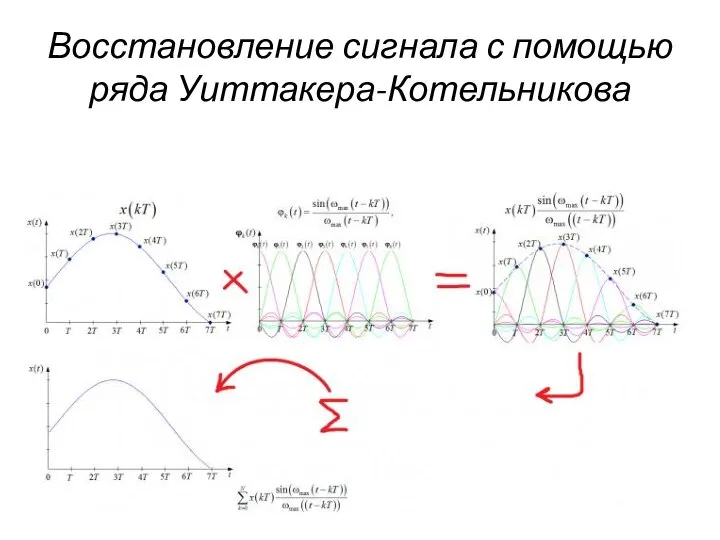
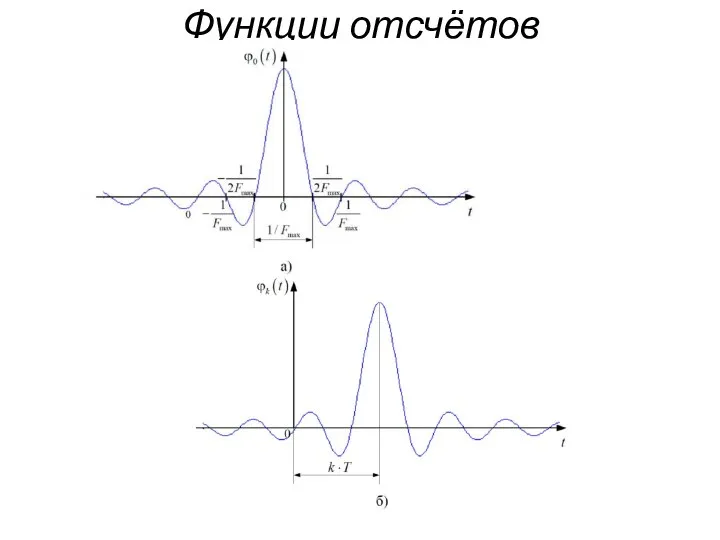
Члены ряда Котельникова представляют собой функции отсчётов, сдвинутых друг относительно друга по времени на величину T, умноженных на величину дискретного значения сигнала x(kt).
Суммирование конечного числа членов ряда позволяет получить сигнал, который будет приближаться к аналоговому сигналу

Ряд Котельникова и Ряд Уиттакера

Теорема отсчетов Котельникова

Функции отсчётов

Восстановление сигнала с помощью ряда Уиттакера-Котельникова

Величина шага отсчета
При малом шаге последовательность отсчетов достаточно точно описывает сигнал, а при большом шаге по отсчетам нельзя восстановит форму сигнала, так как пропущены его характерные экстремальные точки.
Как же часто следует брать отсчеты, чтобы по ним можно было полностью восстановить сигнал?
Ответ на этот вопрос дает теорема, доказанная в 1933 г. Советским ученым академиком В.А.Котельниковым. и названная его именем.
Согласно этой теореме любой непрерывный сигнал с конечным спектром (имеющим максимальное значение ) можно представить в виде дискретных отсчетов , частота дискретизации которых должна быть выбрана не менее чем в два раза выше максимального значения спектра сигнала:, передать его по линии связи, а затем восстановить исходный аналоговый сигнал.

Физический смысл теоремы Котельникова.
Теорема Котельникова утверждает, что если требуется передать непрерывный сигнал с ограниченным спектром по каналу связи, то можно не передавать все его значения: достаточно лишь передать его мгновенные значения (отсчеты) через интервал .
Поскольку сигнал полностью определяется этими значениями, то по ним он может быть восстановлен на приемном конце системы связи.
Для этого достаточно соединить отсчеты плавной кривой. Это можно объяснить тем, что сигнал между отсчетами может изменяться только плавно, так как частоты выше дающие быстрые изменения, в сигнале отсутствуют.
Отсчеты берутся достаточно часто, и тем чаще, чем выше максимальная частота .
Пример
Пусть есть речевой сигнал. Он содержит частоты от 300 Герц до 3 килогерц. Для его передачи по цифровому каналу связи вам потребуется "выхватывать" мгновенные значения этого сигнала с частотой, в два раза превышающей самую высокочастотную компоненту сигнала, т. е. 6 кГц. Иными словами, шесть тысяч раз в секунду вы будете измерять значение сигнала, который изменяется не чаще трех тысяч раз в секунду.

Теорема (Найквиста-Котельникова)
В доказательстве теоремы и далее будет использоваться операция свертки функций I(x), J(x), определяемая так:
Теорема (Найквиста-Котельникова). Для того чтобы сигнал I(x) можно было восстановить по его дискретному образу, его спектр должен быть ограничен максимальной частотой fH и частота дискретизации fs должна быть более 2fH.
Пусть Is(x) - дискретный образ исходного сигнала I(x), как обычно, T = 1/fs - период дискретизации, тогда
Образом функции Comb в частотной области является функция
а Фурье-образ I(x) по-прежнему будем обозначать F(f).
Умножение функций в пространственной области соответствует их свертке (будем обозначать ее * ) в частотной и наоборот.

Теорема
Соответственно, рассмотрим свертку F и FComb, являющуюся Фурье-образом Is(x) (обозначим его Fs(f) ):
(*)
где переход (1) произошел благодаря сдвигающему свойству дельта-функции при свертке. Как видно из последнего выражения, Fs(f) представляет собой бесконечную сумму функций F(f), умноженных на fs и сдвинутых на fs относительно друг друга, поэтому при условии fs > 2fH носители соседних сдвинутых версий не пересекаются, и отдельно, взяв центральную копию F(f) (k = 0) и применив к ней обратное преобразование Фурье, можно получить исходный сигнал I(x). Центральная копия берется путем умножения Fs(f) на прямоугольную функцию где,
Т.е. , - образ исходной функции получен. Заметим, этому умножению в частотной области соответствует свертка в пространственной области.

Интерполяционная формула Найквиста-Шеннона
Применив обратное преобразование Фурье к
получим функцию
Применив свертку с Is(x), получаем
где переход (2) также произошел благодаря сдвигающему свойству дельта-функции при свертке. Последняя формула называется Интерполяционной формулой Найквиста-Шеннона

Пример
Для завершения доказательства осталось показать, что невозможно однозначно восстановить сигнал при .
Приведем соответствующий пример.
Зафиксируем две частоты - fs и fH, ; для упрощения рассуждений предположим, что fs > fH (в общем случае может быть более двух наложений сдвинутых образов, что усложнит построение контрпримера).
Из формулы (*) следует, что Фурье-образ Is(x) является периодической функцией с периодом fs, поэтому вся информация для восстановления содержится в одном периоде (например ).

Пример не однозначности образа
Рассмотрим две функции, Фурье-образы которых равны
(функция однозначно задается своим Фурье-образом). При дискретизации с частотой fs в соответствии с формулой (*)
Фурье-образ в интервале для обеих функций будет равен
Таким образом, в этом случае однозначная реконструкция невозможна.

Искажение сигнала и борьба с этим эффектом
Как было показано при доказательстве теоремы Найквиста-Котельникова, при недостаточной частоте дискретизации восстановленный сигнал будет искажен.
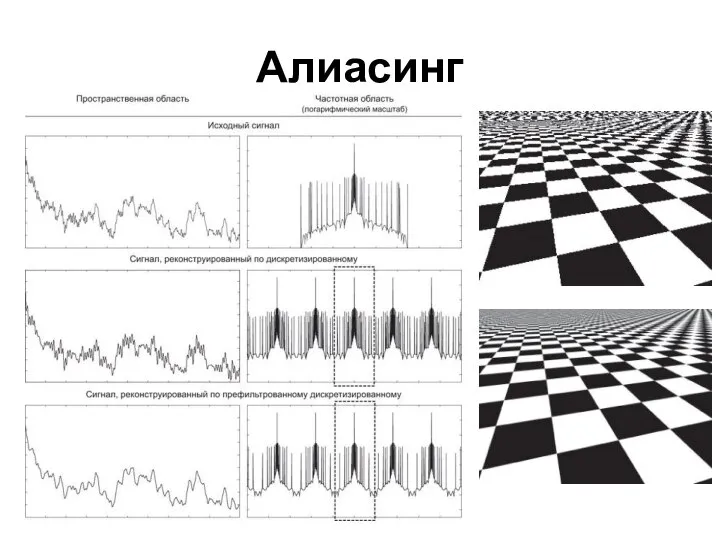
Это наглядно можно наблюдать в частотной области (см. рис.), т.к. при этом копии частотного спектра исходного сигнала будут суммироваться в пересекающихся областях, что даст мнимое увеличение веса компонент с этими частотами в спектре, некую подмену высокочастотных компонент низкочастотными, эффект, известный как алиасинг (англ. aliasing).
Особенно наглядно этот эффект можно наблюдать на резких контрастных изменениях яркости

Алиасинг

Префильтрация
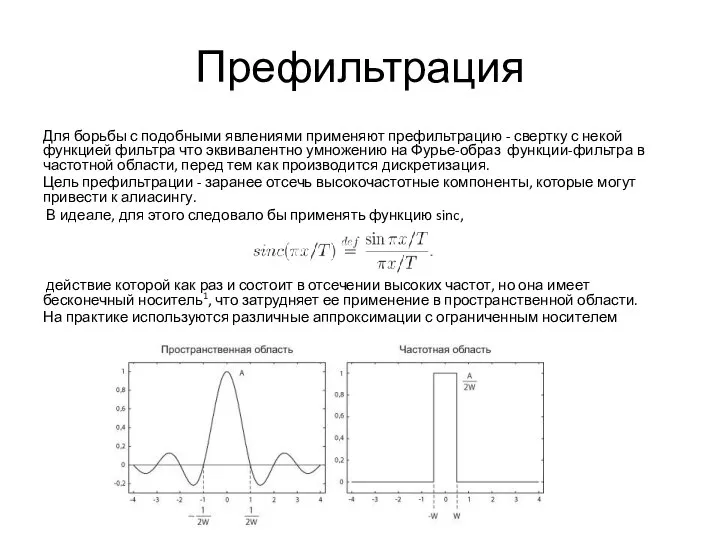
Для борьбы с подобными явлениями применяют префильтрацию - свертку с некой функцией фильтра что эквивалентно умножению на Фурье-образ функции-фильтра в частотной области, перед тем как производится дискретизация.
Цель префильтрации - заранее отсечь высокочастотные компоненты, которые могут привести к алиасингу.
В идеале, для этого следовало бы применять функцию sinc,
действие которой как раз и состоит в отсечении высоких частот, но она имеет бесконечный носитель1, что затрудняет ее применение в пространственной области.
На практике используются различные аппроксимации с ограниченным носителем

Префильтрация
В двумерном случае фильтрация описывается следующим образом: интенсивность пикселя I(x, y) с центром в точке (x, y)будет определяться формулой двумерной свертки
(1)
где F(s, t) - функция фильтра с центром в 0, supp(F) - ее носитель (область, где она не равна 0 ), Img(x, y) - непрерывное аналоговое изображение.

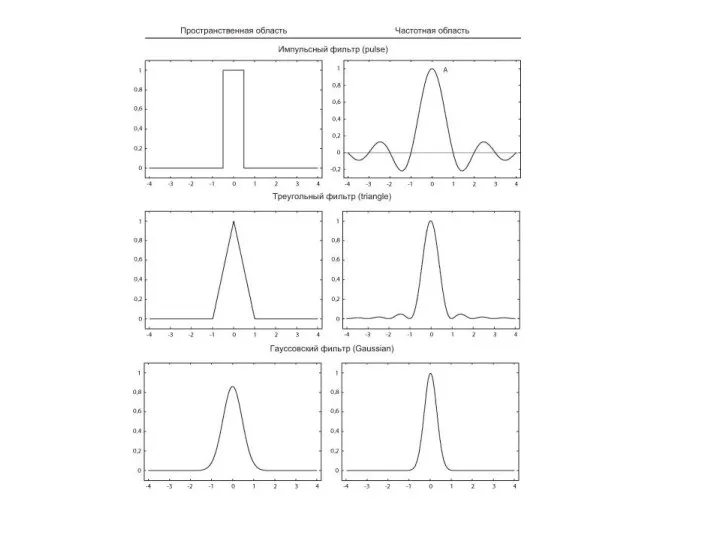
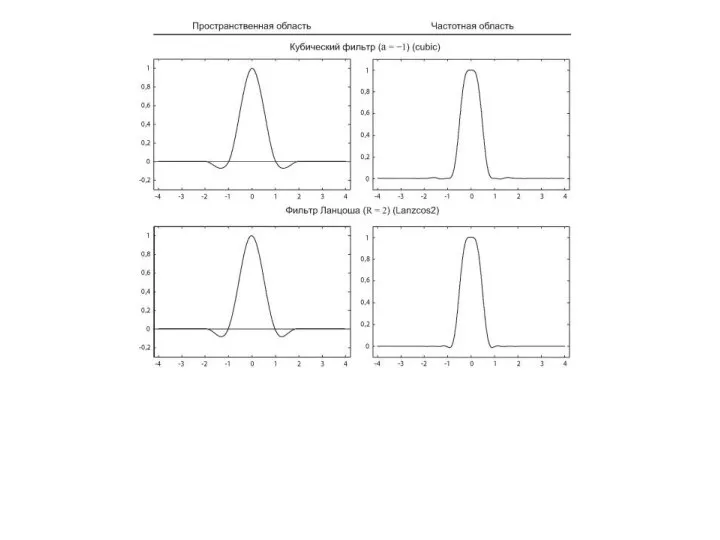
Одномерные функции-фильтры для антиалиасинга

Комментарий
Гауссовский фильтр обычно применяется с (так он лучше всего приближает sinc в частотной области), R берется порядка 2-3.
У кубического фильтра присутствует параметр , с помощью которого можно регулировать степень размытия (увеличение a ) или, наоборот, более четкой передачи краев несмотря на некоторый алиасинг (уменьшение a ), стандарным компромиссным значением является a = -1.
Для Lanzcos, который представляет собой обрезанный и сглаженный sinc, радиус R обычно равен 2 (так называемый Lanzcos2 ), реже - до 4. Большие значения не используются ввиду того, что носитель, а значит, и область интегрирования при свертке, будет слишком большой.
Понятно, что для дискретизации достаточно знать значения префильтрованной функции только в точках дискретизации..

Двумерные аналоги
Двумерные аналоги одномерного фильтра f11(x) строятся двумя путями:
как функция от радиуса:
как произведение:
Первый вариант - более корректный, но второй обладает свойством сепарабельности, т.е. в выражении можно двумерное интегрирование разбить на два одномерных:
В случае передискретизации интегрирование заменяется суммированием и в этом случае быстрее производить вычисления в два этапа, каждый из которых состоит в дискретной свертке по одному измерению и может быть вычислен достаточно эффективно (в том числе и с применением параллельных алгоритмов).
В алгоритмах растеризации с префильтрацией более популярны фильтры первого типа, а для геометрических преобразований, где происходит передискретизация - второго.

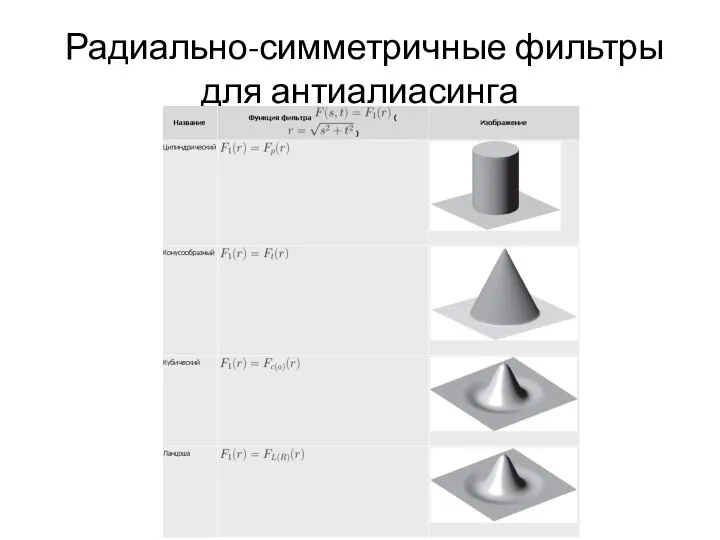
Радиально-симметричные фильтры для антиалиасинга

Одномерные функции-фильтры для антиалиасинга

Комментарий
Двумерные аналоги фильтров, приведены в (для простоты частота дискретизации равна 1, произвольный случай получается масштабированием по осям).
Прямоугольный фильтр соответствует либо цилиндру (первый тип), либо параллелепипеду с квадратным основанием (англ. Box filter) (второй тип);
треугольный соответствует либо конусу, либо пирамиде соответственно.
По смыслу прямоугольные и треугольные аналоги соответствуют так называемым невзвешенной и взвешенной площадным выборкам.
Если рассмотреть Фурье-образы их одномерных аналогов на , можно заметить, что взвешенная площадная выборка лучше отфильтровывает высокие частоты, поэтому рекомендуется применять именно ее.

Антиалиасинг или Фильтрация-сглаживание
(англ. antialiasing) - устранение видимых артефактов дискретизации, особенно для изображений линий или краев объектов. Возможны два основных подхода.
Учет эффектов дискретизации в алгоритмах построения изображений. То есть, фактически, встраивание в них префильтрации.
Адаптивная дискретизация с постфильтрацией.
Получение нового дискретизированного изображения по другому дискретизированному с помощью дискретной фильтрации, т.н. постфильтрации.
Данный подход может быть эффективен при переходе от промежуточной большей частоты дискретизации к меньшей.
Процесс растеризации с увеличенной по отношению к требуемой частотой первичной дискретизации с последующей постфильтрацией называется супердискретизацией (англ. supersampling).
Первичная частота дискретизации может варьироваться в разных частях изображения в зависимости от его свойств.

Растеризация с антиалиасингом
При растеризации абстрактно определенных примитивов (точек, линий, многоугольников) можно рассматривать их как двумерный сигнал и применить к нему префильтрацию как описано в предыдущем разделе.
В качестве одной из моделей понятия растра рассматривалось замощение плоскости, где каждый пиксель представляет собой квадрат. При растеризации этому квадрату нужно приписать цвет так, чтобы при взгляде на изображение растра на каком-либо устройстве вывода воспринимаемая картинка была наиболее похожа на исходный непрерывный двумерный сигнал.
Заметим, что выражение (1) линейно по Img и, следовательно, обладает свойством суперпозиции по отношению к Img.
Т.е. если Img состоит из нескольких непересекающихся объектов, то в (1) достаточно будет просуммировать вклад от этих объектов.
Понятно, что с увеличением радиуса фильтра изображение будет все более сглаженным и даже размытым, а с уменьшением радиуса уменьшится его эффект для антиалиасинга.

Алгоритм Гупты-Спрулла
Данный алгоритм для растеризации отрезков с целочисленными координатами концов был предложен Гуптой и Спруллом .
В нем предполагается использование радиально-симметричного фильтра (такого как конический).
Пусть его радиус равен R. Для того чтобы выяснить, каким цветом следует закрасить пиксель, необходимо посчитать значение свертки фильтра с функцией прямой ( I = 1 в вытянутом прямоугольнике толщиной t и 0 вне него), см. рис.

Алгоритм Гупты-Спрулла
Обозначим результат этой операции FR,t(r), где r - расстояние от центра закрашиваемого пикселя до центральной оси прямой.
Заметим, что FR,t(r) = 0 для r > R + t/2.
Идея алгоритма состоит в модификации алгоритма Брезенхема для одновременной закраски нескольких пикселей разной интенсивности в столбце.
Так же, как и в алгоритме Брезенхема, речь идет о случае наклона прямой меньше чем на 45.
Случай вертикального наклона аналогично просто сводится к первому случаю.

Алгоритм Гупты-Спрулла
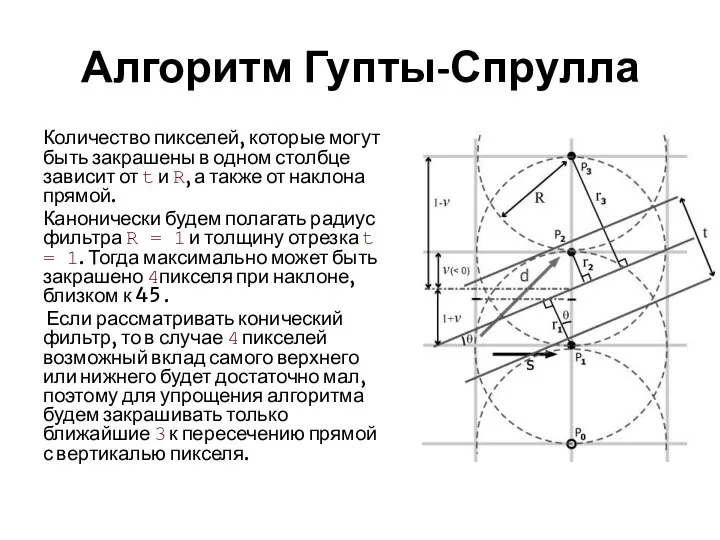
Количество пикселей, которые могут быть закрашены в одном столбце зависит от t и R, а также от наклона прямой.
Канонически будем полагать радиус фильтра R = 1 и толщину отрезка t = 1. Тогда максимально может быть закрашено 4пикселя при наклоне, близком к 45 .
Если рассматривать конический фильтр, то в случае 4 пикселей возможный вклад самого верхнего или нижнего будет достаточно мал, поэтому для упрощения алгоритма будем закрашивать только ближайшие 3 к пересечению прямой с вертикалью пикселя.

Алгоритм Гупты-Спрулла

Алгоритм Гупты-Спрулла
Пусть функция round находит номер интервала по действительному значению в [0,R + t/2]. Тогда, модифицируя алгоритм Брезенхема, получаем следующий алгоритм:
// plot(x,y,I) закрашивает пиксель (x,y) с интенсивностью I
e = 2b - a;
Delta eS = 2b;
Delta eD = 2b - 2a;
denom = 1/(2*sqrt(a*a+b*b));
fixPart = 2a*denom;
// фикс. часть r_1 и r_3
// (x,y) - Координаты текущей точки
x= 0; y = 0; while( x < a ) { av2 = (e+a)*denom;
plot(x, y-1, ITable[round(fixPart+av2)] );
plot(x, y, ITable[round(abs(av2))] );
plot(x, y+1, ITable[round(fixPart-av2)] );
if( e > 0 ) {
// d : диагональное смещение
x++;
y++; e += Delta eD; } else {
// s : горизонтальное смещение
x++; e += Delta eS; } }