Двоичная система счисления.Количество информации.

Единица измерения количества информации
За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающие неопределенность в два раза.
Такая единица называется «Бит».

Количество возможных событий и количество информации.
N=2I
где N – количество возможных событий. I – количество информации.

Например:
Если мы получили 4 бита информации, то количество возможных событий составило:
N = 24 = 16
При игре «Крестики-нолики» на поле 8х8 перед первым ходом существует 64 возможных события (64 различных варианта расположения «крестика»):
64=2I,
так как 64=26, то получим:
26=2I,
Следовательно I=6 битов.

Кодирование информации
Кодирование – это операция преобразования знаков или групп знаков одной знаковой системы в знаки или группы знаков другой знаковой системы.

Двоичное кодирование информации в компьютере
У компьютера для кодирования информации применяется только два бесспорных состояния логических элементов или выключено, или включено. Посему, в двоичном счете имеется всего лишь только две цифры со значениями 0 и 1.
Пакет двоичных цифр от 00000000 до 11111111 – 1 байт.
1байт = 8 бит

Перевод числа из одной системы счисления в другую.
Представим десятичное число 446 в следующем виде
44610=400+40+6=4*102+4*101+6*100
Пусть дано число, в котором N цифр. i-ю цифру обозначим через ai, число примет вид anan-1….a2a1
anan-1….a2a1 = an*10n-1+an-1*10n-2 + …. + a2*101+a1*100
ai – символы из набора "0123456789"

Заменим 10 на 2 и получим формулу для определения двоичного числа:
anan-1….a2a1 = an * 2n-1 + an-1 * 2n-2 + …. + a2 * 21 + a1 * 20
где ai это символ из набора "01"
1012 = 1*22 + 0*21 + 1*20 = 4+0+1=510
110012 = 1*24+1*23+0*22+0*21+1*20=16+8+0+0+1=2510

Для того, чтобы преобразовать десятичное число в двоичное, его нужно разложить по степеням двойки.
Пример: 3510
22 (4), 23(8), 24(16),25(32) –мало, 26(64) - много, оставляем 25(32)
35 - 25(32) = 3, остаток 3
представим в виде степени двойки 3
3 - 21(2) = 1, остаток 1
представим в виде степени двойки 1
1 - 20(1) = 0
Старшая степень была 5, следовательно в уравнении должно быть (n-1=5, n=6) шесть слагаемых. Уравнение примет вид:
3510=1*25 + 0*24 + 0*23 + 0*22 + 1*21 + 1*20=1000112

Разложим приведенным выше методом 4410
25(32) < 44<26(64) – ближайшая степень двойки 5, следовательно двоичное число будет состоять из 6 знаков.
44 - 25(32) = 12, остаток 12.
Представим в виде степени двойки 12, ближайшая степень 3
12 - 23(8) = 4, остаток 4.
Представим в виде степени двойки 4, ближайшая степень 2
4 - 22(4)=0, остаток 0.
В уравнении будет 6 слагаемых:
4410 = 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 0*20=1011002

Рассмотрим ещё один способ перевода целого десятичного числа в двоичную систему счисления
AЦД = an * 2n-1 + an-1 * 2n-2 + …. + a2 * 21 + a1 * 20
Разделим AЦД на основание двоичной системы (на 2). Частное от деления будет an* 2n-2 + an-1* 2n-3 + …. + a2
а остаток равен a1
Разделив на втором шаге целое частное число ещё на 2 остаток будет равен a2
После N-ого шага деления получаем последовательность остатков
a1 a2 a3….. an
Эта последовательность совпадает с обратной последовательность цифр целого двоичного числа
А2= an an-1..... a2a1

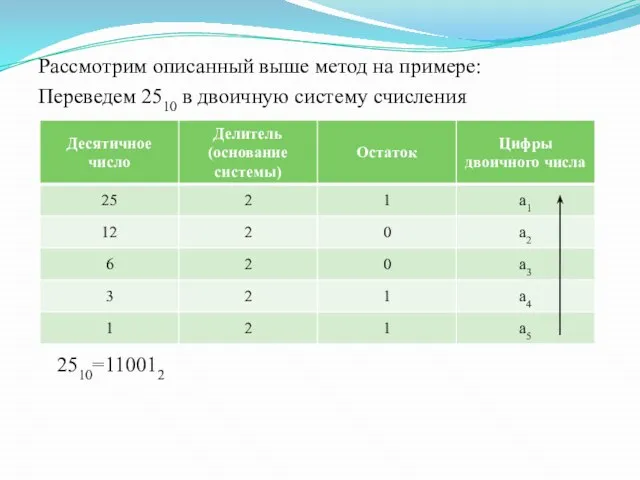
Рассмотрим описанный выше метод на примере:
Переведем 2510 в двоичную систему счисления
2510=110012

Сложение двоичных чисел на примере: 100112 + 100012.
Первый разряд: 1+1 = 2. Записываем 0 и 1 на ум пошло.
Второй разряд: 1+0+1(запомненная единица) =2. Записываем 0 и 1 на ум пошло.
Третий разряд: 0+0+1(запомненная единица) = 1. Записываем 1.
Четвертый разряд 0+0=0. Записываем 0.
Пятый разряд 1+1=2. Записываем 0 и добавляем к шестым разрядом 1.

Вычитание двоичных чисел на примере 11102-1012
Первый разряд. 0-1. Не хватает единицы. Занимаем её в старшем разряде. Единица из старшего разряда переходит в младший, как две единицы (потому что старший разряд представляется двойкой большей степени) 2-1 =1. Записываем 1.
Второй разряд. Единицу этого разряда мы занимали, поэтому сейчас в разряде 0.
0-0=0. Записываем 0.
Третий разряд. 1-1=0. Записываем 0.
Четвертый разряд. От 1 нечего отнимать. Записываем 1.

Умножение двоичных чисел на примере 10112 * 1012
Это умножение можно свести к сумме трёх порязрядных умножений:
1011 * 1 + 1011 * 0 + 1011 * 100 = 1011 +101100 = 110111

Деление двоичных чисел на примере 1010001012/11012

Самостоятельная работа
1. Перевести в двоичную систему счисления:
7510, 3810, 2510
2. Перевести в десятичную систему счисления:
10012, 110012, 11112
3. Вычислить и перевести ответ в десятичную систему счисления следующие выражения (Пример ответа – А10 (B2) ):
А. 110012+11112, 10002+1002
Б. 111100112 – 100101112, 1000010002 – 101100112
В. 11102 * 10102, 11112 * 10012
Г. 1110100010012 : 1111012, 1011110011012 : 1101012
Удачи!

Ответы:
1. 10010112 , 1001102 , 110012
2. 910, 2510, 1510
3. А. 4010 (1010002), 1210 (11002)
Б. 9210(10111002), 8910(10101012)
В. 14010(100011002), 13510(100001112)
Г. 6110(1111012), 5710(1110012)