Электростатика

2.1. Силовые линии электростатического поля
2.2. Поток вектора напряженности
2.3. Теорема Остроградского-Гаусса
2.4. Дифференциальная форма теоремы2.4. Дифференциальная форма теоремы 2.4. Дифференциальная форма теоремы Остроградского-Гаусса
2.5. Вычисление электростатических полей с помощью теоремы Остроградского-Гаусса
2.5.1. Поле бесконечной однородно заряженной плоскости
2.5.2. Поле двух равномерно заряженных плоскостей
2.5.3. Поле заряженного бесконечного цилиндра (нити)
2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью заряда, но разным знаком
2.5.5. Поле заряженного пустотелого шара
2.5.6. Поле объемного заряженного шара
Тема 2. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА
2.1. Силовые линии электростатического поля
2.2. Поток вектора напряженности
2.3. Теорема Остроградского-Гаусса
2.4. Дифференциальная форма теоремы2.4. Дифференциальная форма теоремы 2.4. Дифференциальная форма теоремы Остроградского-Гаусса
2.5. Вычисление электростатических полей с помощью теоремы Остроградского2.5. Вычисление электростатических полей с помощью теоремы Остроградского 2.5. Вычисление электростатических полей с помощью теоремы Остроградского -2.5. Вычисление электростатических полей с помощью теоремы Остроградского - 2.5. Вычисление электростатических полей с помощью теоремы Остроградского - Гаусса
2.5.1. Поле бесконечной однородно заряженной плоскости
2.5.2. Поле двух равномерно заряженных плоскостей
2.5.3. Поле заряженного бесконечного цилиндра (нити)
2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью заряда, но разным знаком
2.5.5. Поле заряженного пустотелого шара
2.5.6. Поле объемного заряженного шара

2.1. Силовые линии электростатического поля
Теорема Остроградского-Гаусса, которую мы докажем и обсудим позже, устанавливает связь между электрическими зарядами и электрическим полем. Она представляет собой более общую и более изящную формулировку закона Кулона.

Остроградский Михаил Васильевич (1801 – 1862)
отечественный математик и механик. Учился в Харьковском ун-те (1816 – 1820), совершенствовал знания в Париже (1822 – 1827).
Основные работы в области математического анализа, математической физики, теоретической механики. Решил ряд важных задач гидродинамики, теории теплоты, упругости, баллистики, электростатики, в частности задачу распространения волн на поверхности жидкости (1826 г.). Получил дифференциальное уравнение распространения тепла в твердых телах и жидкостях. Известен тео­ремой Остроградского-Гаусса в электро­статике (1828 г.).

Гаусс Карл Фридрих (1777 – 1855) немецкий математик, астроном и физик.
Исследования посвящены многим разделам физики.
В 1832 г. создал абсолютную систему мер (СГС), введя три основных единицы: единицу времени – 1 с, единицу длины – 1 мм, единицу массы – 1 мг.
В 1833 г. совмест­но с В. Вебером построил первый в Герма­нии электромагнитный телеграф.
Еще в 1845 г. пришел к мысли о конечной скорости распростране­ния электромагнитных взаимодействий. Изу­чал земной магнетизм, изобрел в 1837 г. униполярный магнитометр, в 1838 г. – бифилярный. В 1829 г.
Сформулировал принцип наименьшего принуждения (принцип Гаусса).
Один из первых высказал в 1818 г. предположение о возможности существования неевклидовой геометрии.

Основная ценность теоремы Остроградского-Гаусса состоит в том, что она позволяет глубже понять природу электростатического поля и устанавливает более общую связь между зарядом и полем.

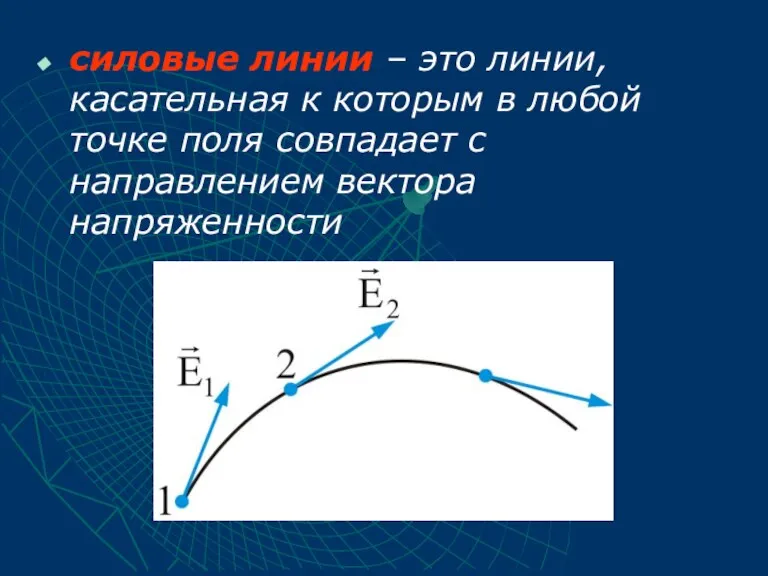
силовые линии – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности

Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению, т.е. Однородное электростатическое поле изображается параллельными силовыми линиями на равном расстоянии друг от друга

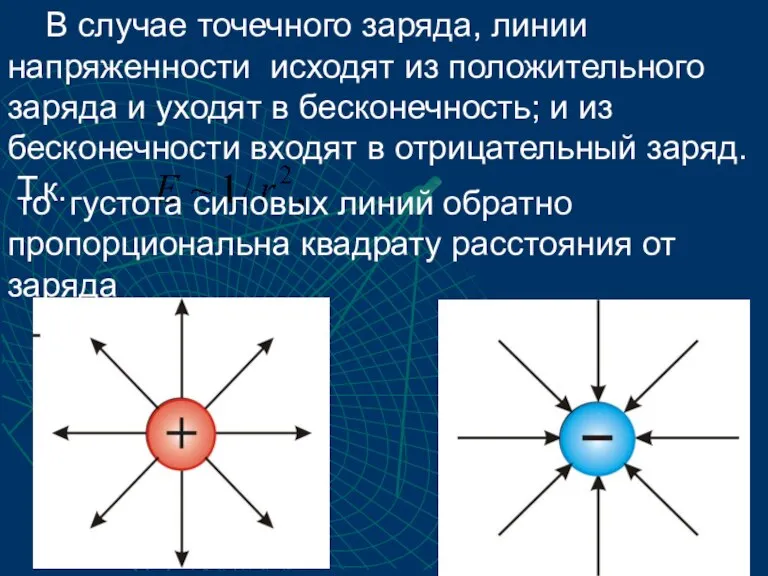
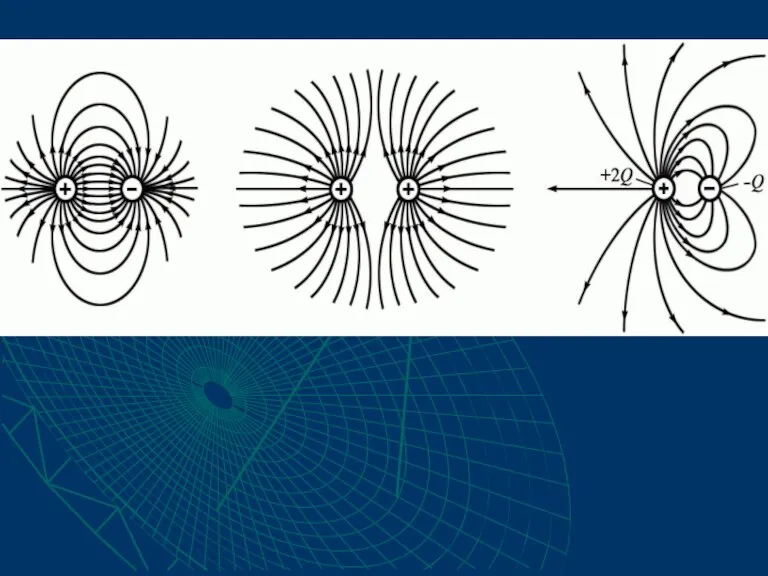
В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в бесконечность; и из бесконечности входят в отрицательный заряд.
Т.к.
то густота силовых линий обратно пропорциональна квадрату расстояния от заряда

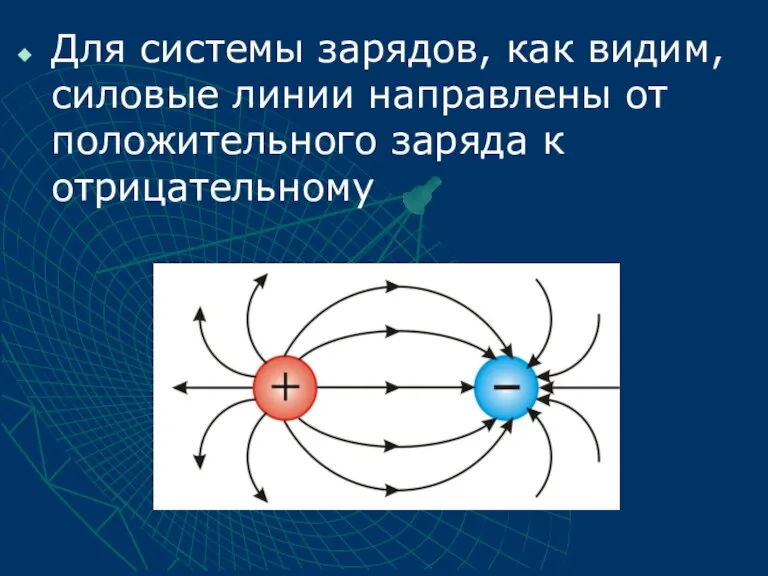
Для системы зарядов, как видим, силовые линии направлены от положительного заряда к отрицательному

Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к вектору напряженности пересекало такое их число, которое равно модулю вектора напряженности , т.е.

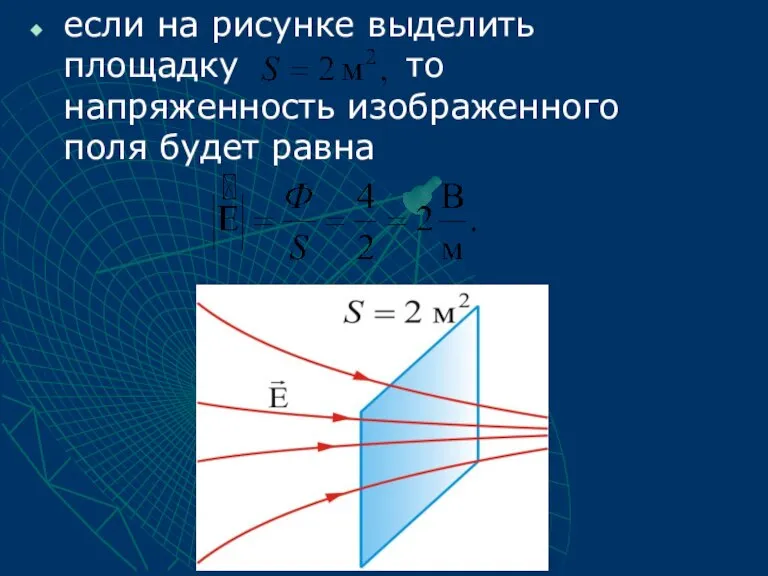
если на рисунке выделить площадку то напряженность изображенного поля будет равна

2.2. Поток вектора напряженности
Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф через эту поверхность
В векторной форме можно записать – скалярное произведение двух векторов, где вектор .

Таким образом, поток вектора есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.

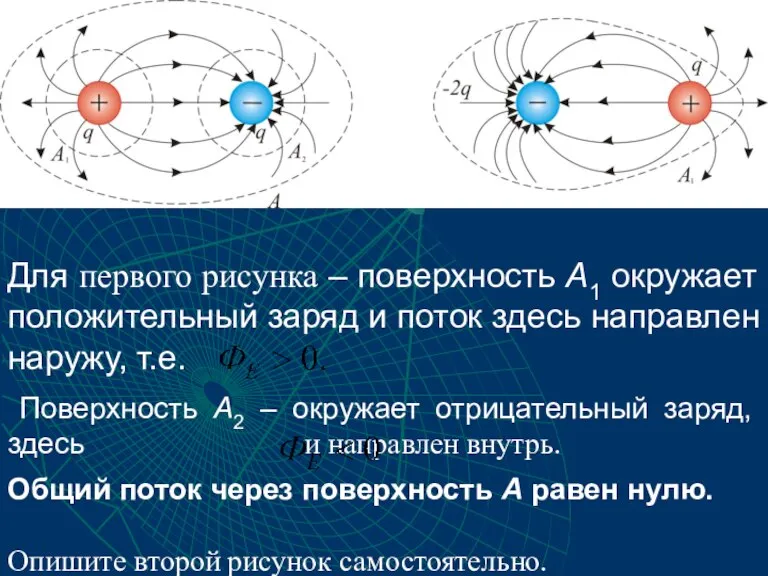
Для первого рисунка – поверхность А1 окружает положительный заряд и поток здесь направлен наружу, т.е.
Поверхность А2 – окружает отрицательный заряд, здесь и направлен внутрь.
Общий поток через поверхность А равен нулю.
Опишите второй рисунок самостоятельно.

2.3. Теорема Остроградского-Гаусса
Итак, по определению, поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность S.

поток вектора напряженности через произвольную элементарную площадку dS будет равен:
Т.е. в однородном поле
В произвольном электрическом поле

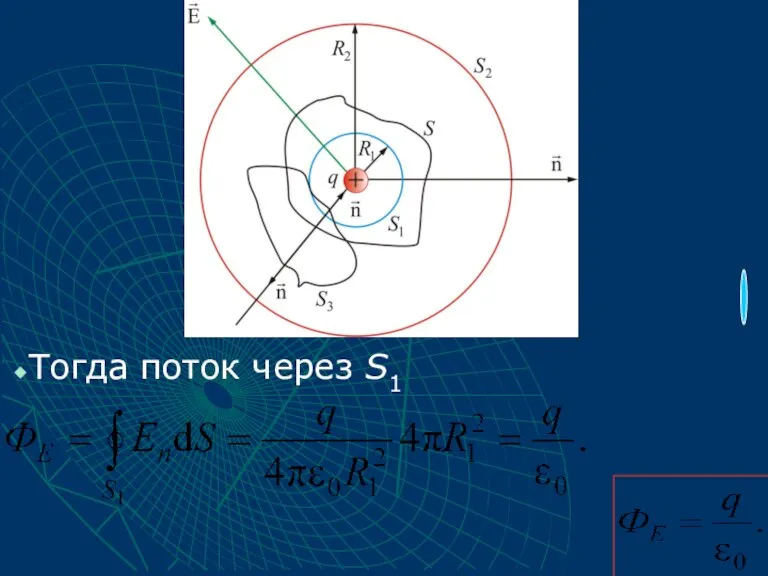
Подсчитаем поток вектора через произвольную замкнутую поверхность S, окружающую точечный заряд q . Окружим заряд q сферой S1.

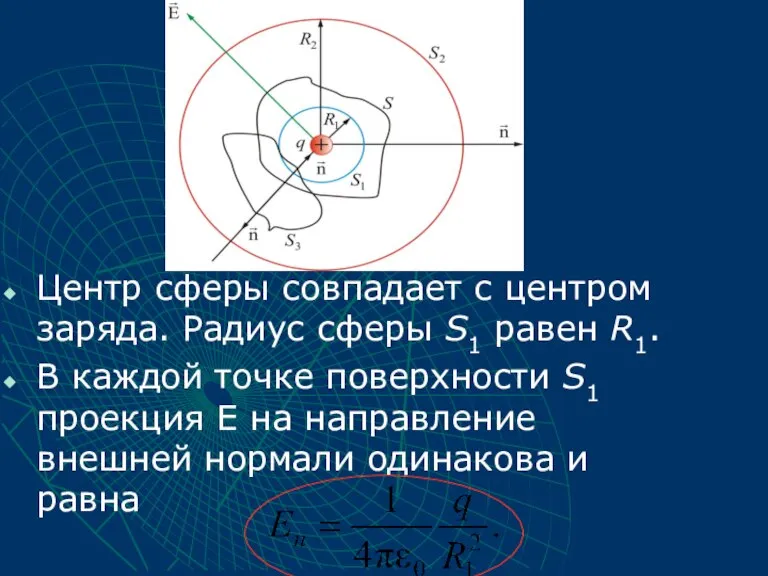
Центр сферы совпадает с центром заряда. Радиус сферы S1 равен R1.
В каждой точке поверхности S1 проекция Е на направление внешней нормали одинакова и равна

Тогда поток через S1

Подсчитаем поток через сферу S2, имеющую радиус R2:

Из непрерывности линии следует, что поток и через любую произвольную поверхность S будет равен этой же величине:
– теорема Гаусса для одного заряда.

Для любого числа произвольно расположенных зарядов, находящихся внутри поверхности:
– теорема Гаусса для нескольких зарядов.
Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0.

Полный поток проходящий через S3, не охватывающую заряд q, равен нулю:

Таким образом, для точечного заряда q, полный поток через любую замкнутую поверхность S будет равен:
– если заряд расположен внутри замкнутой поверхности;
– если заряд расположен вне замкнутой поверхности;
этот результат не зависит от формы поверхности, и знак потока совпадает со знаком заряда.

Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах пространства:
Здесь dV – физически бесконечно малый объем, под которым следует понимать такой объем, который с одной стороны достаточно мал, чтобы в пределах его плотность заряда считать одинаковой, а с другой – достаточно велик, чтобы не могла проявиться дискретность заряда, т.е. то, что любой заряд кратен целому числу элементар-ных зарядов электрона или протона .

Суммарный заряд объема dV будет равен:
Тогда из теоремы Гаусса можно получить:
– это ещё одна форма записи теоремы Остроградского-Гаусса, если заряд неравномерно распределен по объему.

2.4. Дифференциальная форма теоремы Остроградского-Гаусса
Пусть заряд распределен в пространстве ΔV, с объемной плотностью . Тогда

Теперь устремим , стягивая его к интересующей нас точке. Очевидно, что при этом будет стремиться к ρ в данной точке, т.е.
Величину, являющуюся пределом отношения к ΔV, при , называют дивергенцией поля Е и обозначается .

Дивергенция поля Е
. (2.4.1)
Аналогично определяется дивергенция любого другого векторного поля.
Из этого определения следует, что дивергенция является скалярной функцией координат.
В декартовой системе координат

Итак,
(2.4.3)
Это теорема Остроградского-Гаусса в дифференциальной форме.
Написание многих формул упрощается, если ввести векторный дифференциальный оператор (Набла)
где i, j, k – орты осей (единичные векторы).

Сам по себе оператор смысла не имеет. Он приобретает смысл в сочетании с векторной или скалярной функцией, на которую символично умножается:
дифференциальная форма теоремы Остроградского-Гаусса.

В тех точках поля, где – (положительные заряды) источники поля,
где – стоки (отрицательные заряды).
Линии выходят из источников и заканчиваются в стоках.

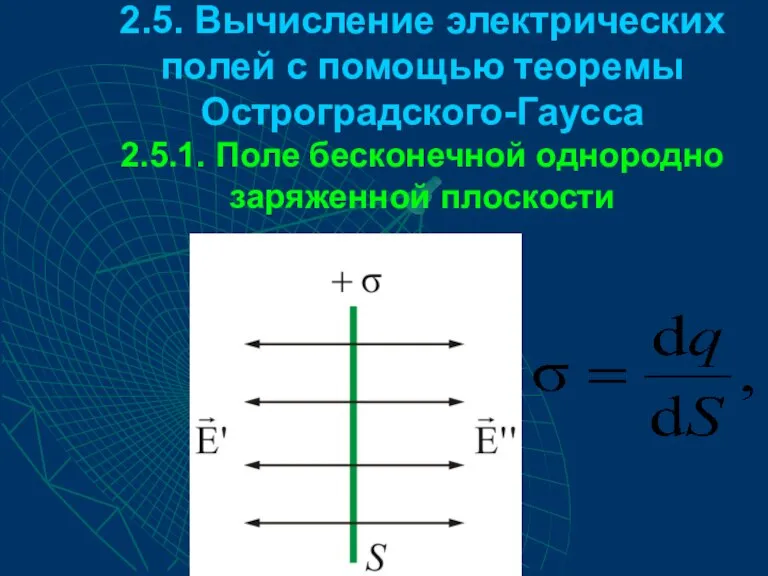
2.5. Вычисление электрических полей с помощью теоремы Остроградского-Гаусса
2.5.1. Поле бесконечной однородно заряженной плоскости

Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:
dq – заряд, сосредоточенный на площади dS;
dS – физически бесконечно малый участок поверхности.

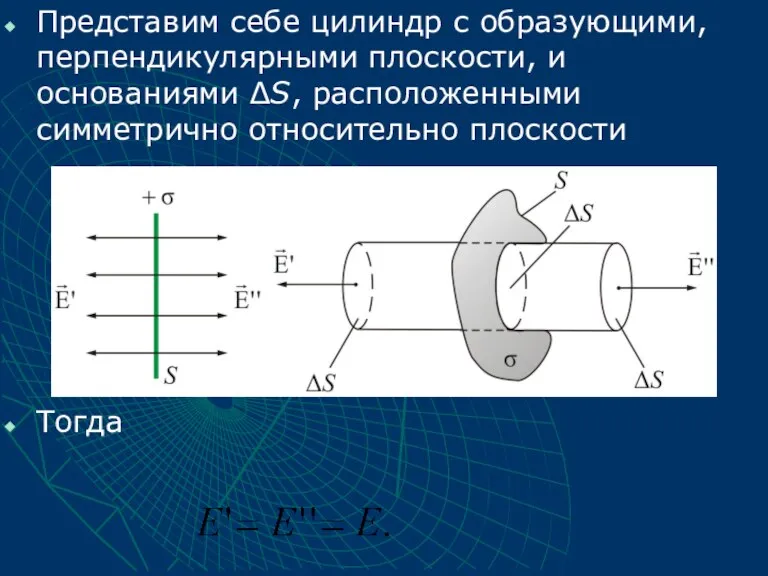
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости
Тогда

Суммарный поток через замкнутую поверхность (цилиндр) будет равна:
Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского-Гаусса получим:
откуда видно, что напряженность поля плоскости S равна:
(2.5.1)

2.5.2. Поле двух равномерно заряженных плоскостей
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ

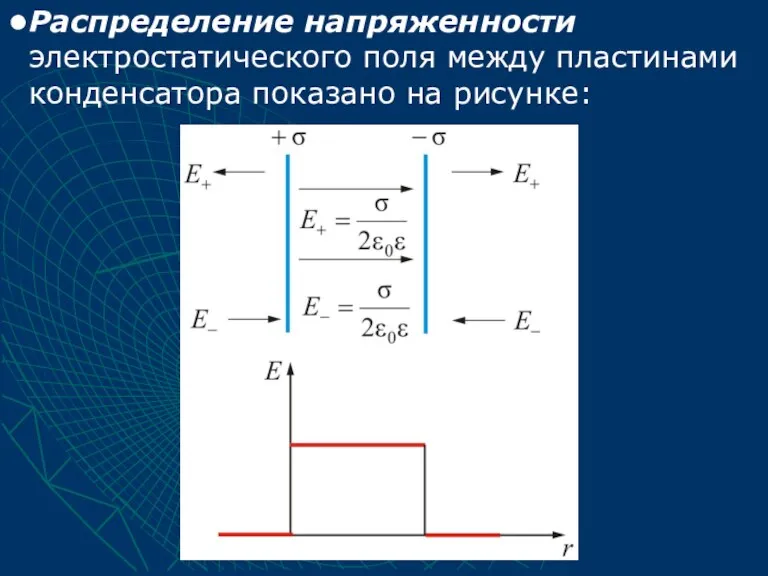
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей
Вне плоскостей напряженность поля
Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).

Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке:

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
т.е.
Механические силы, действующие между заряженными телами, называют пондермоторными.

Сила притяжения между пластинами конденсатора:
где S – площадь обкладок конденсатора.
Т.к.
Это формула для расчета пондермоторной силы

2.5.3. Поле заряженного бесконечного цилиндра (нити)
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью
где dq – заряд, сосредоточенный на отрезке цилиндра

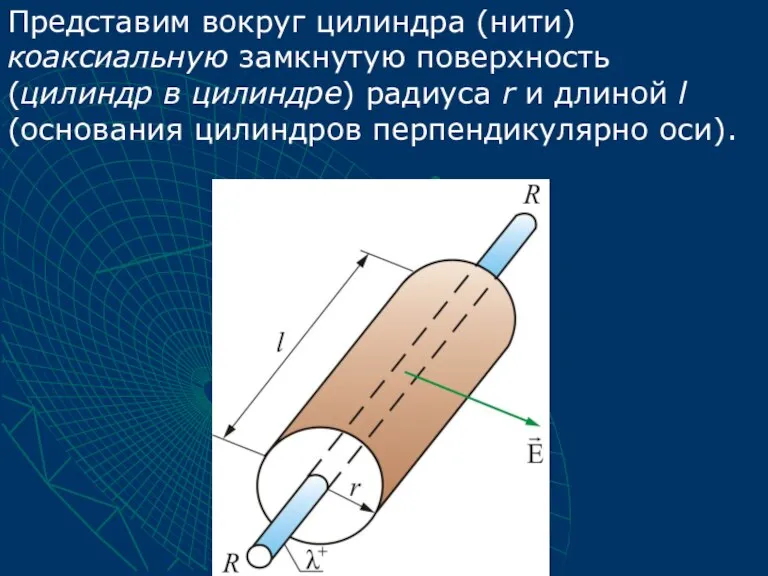
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси).

Для оснований цилиндров
для боковой поверхности т.е. зависит от расстояния r.
Следовательно, поток вектора через рассматриваемую поверхность, равен

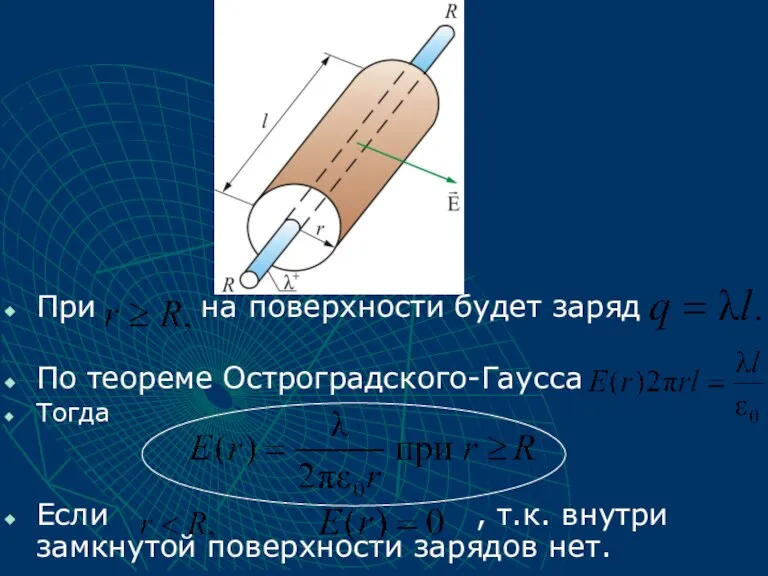
При на поверхности будет заряд
По теореме Остроградского-Гаусса
Тогда
Если , т.к. внутри замкнутой поверхности зарядов нет.

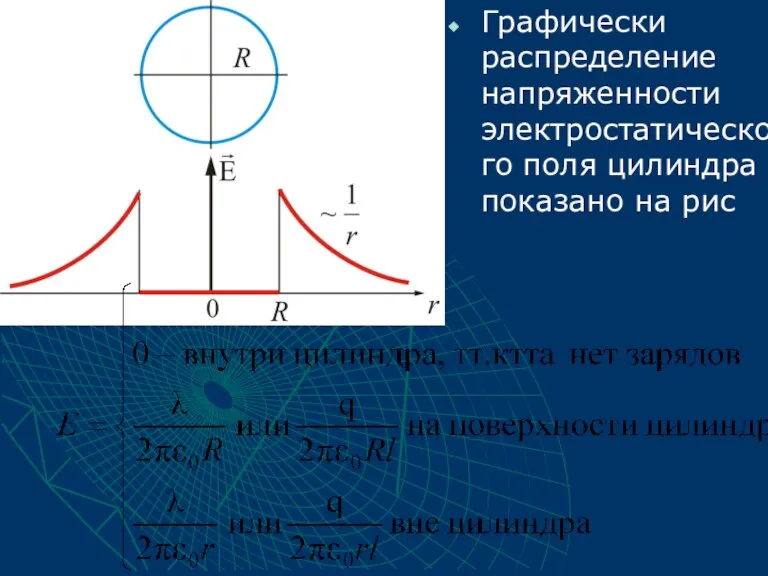
Графически распределение напряженности электростатического поля цилиндра показано на рис

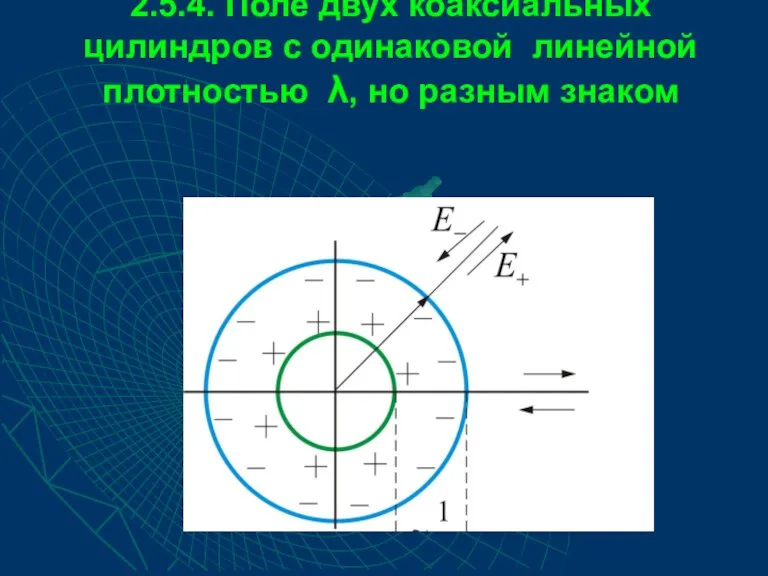
2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком

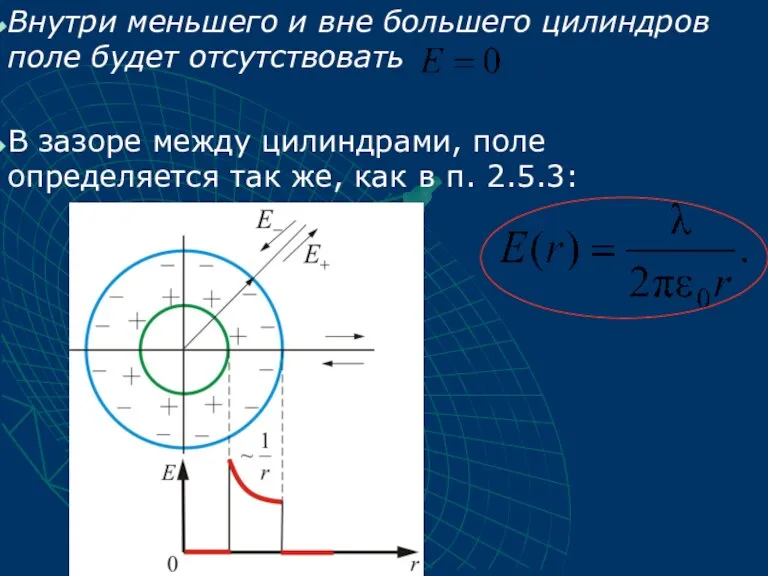
Внутри меньшего и вне большего цилиндров поле будет отсутствовать
В зазоре между цилиндрами, поле определяется так же, как в п. 2.5.3:

Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).
Таким образом для коаксиальных цилиндров имеем:

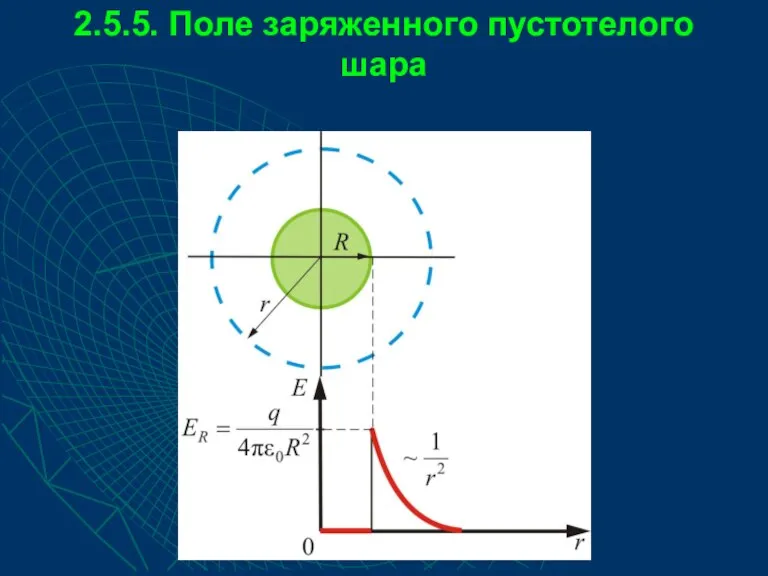
2.5.5. Поле заряженного пустотелого шара

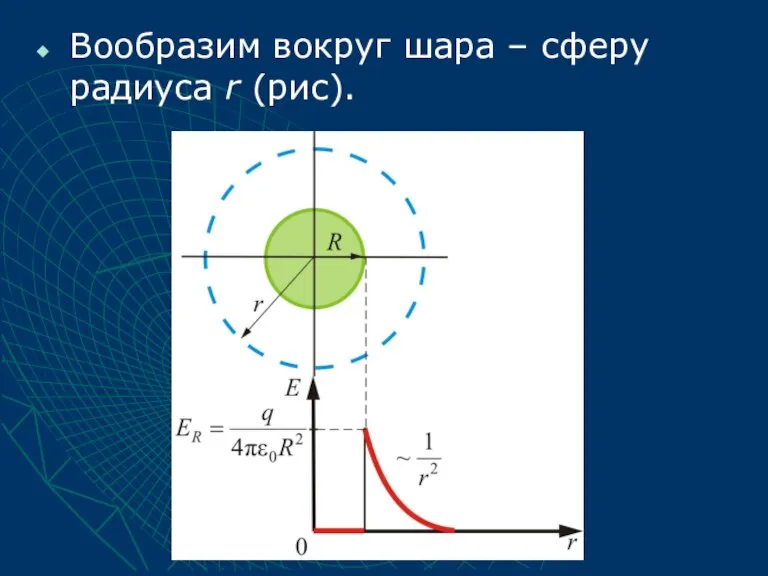
Вообразим вокруг шара – сферу радиуса r (рис).

Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
откуда поле вне сферы:
Внутри сферы, при поле будет равно нулю, т.к. там нет зарядов:

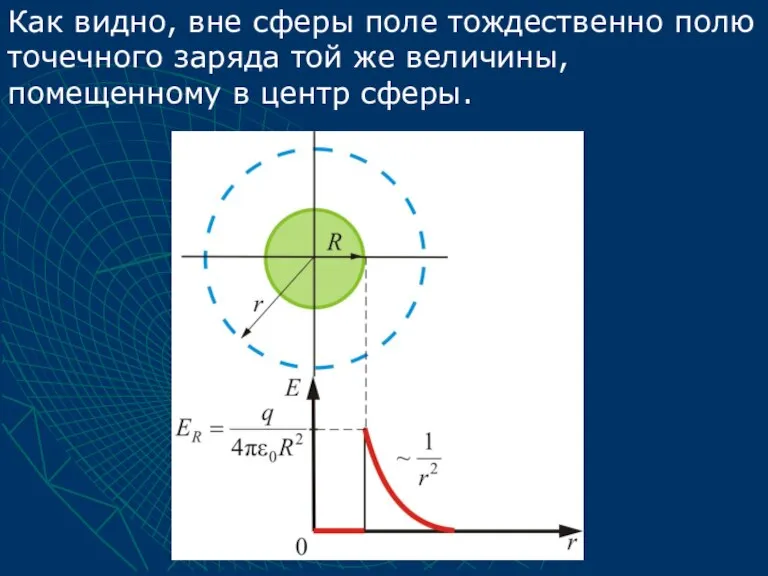
Как видно, вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.

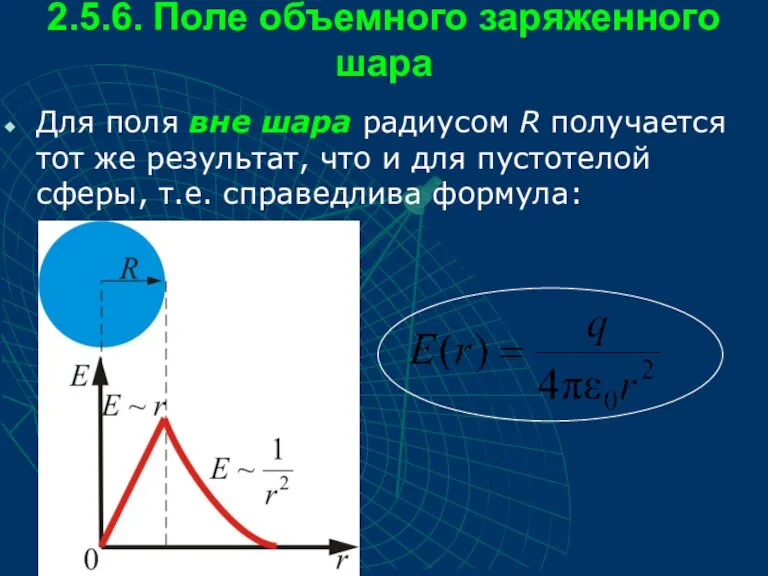
2.5.6. Поле объемного заряженного шара
Для поля вне шара радиусом R получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула:

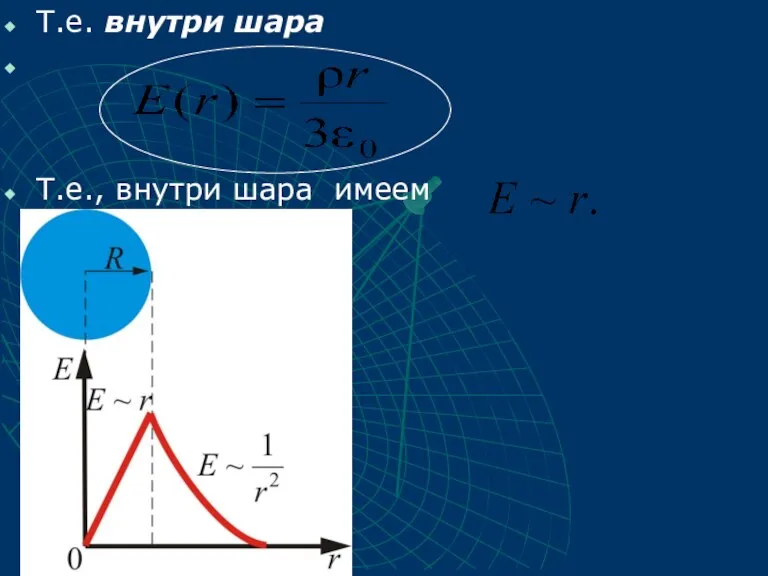
Внутри шара при сферическая поверхность будет содержать в себе заряд, равный
где ρ – объемная плотность заряда: объем шара:
Тогда по теореме Остроградского-Гаусса запишем

Т.е. внутри шара
Т.е., внутри шара имеем

Таким образом, имеем:
поле объемного заряженного шара