Содержание
- 2. Фигура. Мера, диаметр фигуры. Ранг дробления Под фигурой будем понимать один из следующих геометрических объектов: I.
- 3. Определение 2.
- 4. Определение 3. Диаметром фигуры называется максимальное расстояние между двумя любыми точками фигуры Пример 1.
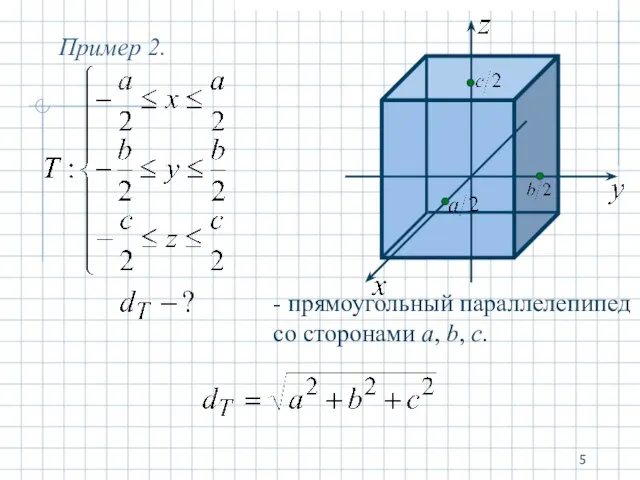
- 5. Пример 2. - прямоугольный параллелепипед со сторонами a, b, c.
- 6. В дальнейшем будем часто использовать следующий прием: разбиение (дробление) фигуры Ф на n непересекающихся областей Ф1,
- 7. Задача о вычислении массы фигуры Рассмотрим фигуру Ф. I. Если Ф однородная фигура, то Решение -
- 8. II. Если Ф - неоднородная фигура Выполним следующие действия: 1. Разобьем Ф на Ф1, Ф2, …
- 9. - приближение!
- 10. - точный результат 4. Вычисление массы mФ
- 11. Определение интеграла по фигуре Выполним последовательность действий, аналогичную п. 2. 1. Разобьем Ф на Ф1, Ф2,
- 12. 3. Организуем последовательность дроблений имеем последовательность интегральных сумм Определение. Интегралом функции f(P) на фигуре Ф называется
- 13. Теорема (о существовании интеграла по фигуре) Если то существует интеграл по фигуре 1. функция f(P) непрерывна
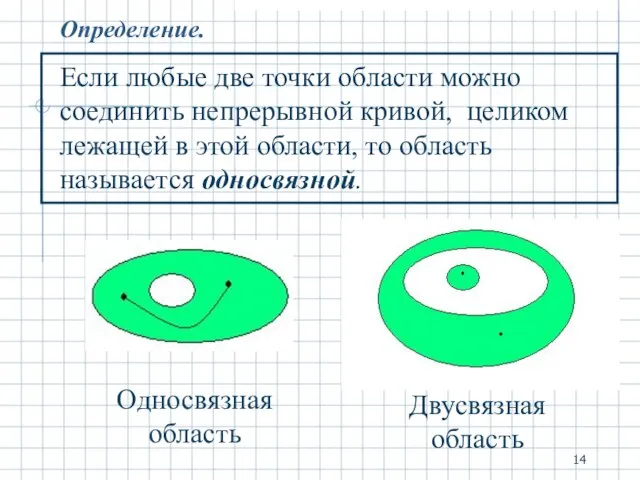
- 14. Определение. Если любые две точки области можно соединить непрерывной кривой, целиком лежащей в этой области, то
- 15. Классификация интегралов по фигуре - определенный интеграл 2. Ф – дуга линии L - криволинейный интеграл
- 16. - двойной интеграл - площадь элементарной поверхности - поверхностный интеграл первого рода
- 17. - тройной интеграл Фигура – пространственная область
- 18. Механический смысл интегралов по фигуре см.вопрос 2
- 19. Геометрический смысл интегралов по фигуре Из пункта 4 В частности: Полученными формулами необходимо уметь пользоваться и
- 20. Свойства интегралов, выраженные равенствами 1. Доказываются с помощью определения! 2. линейность 3. - аддитивность
- 21. Свойства интегралов, выраженные неравенствами 2. Если то то
- 22. 3. Если то
- 24. Скачать презентацию


















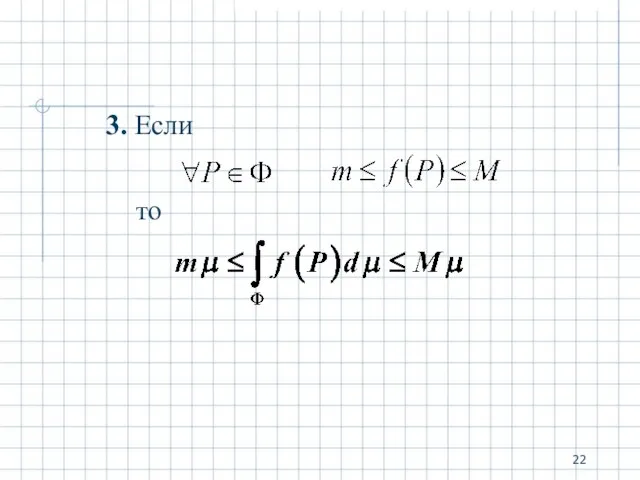
 Коммуникативная грамматика
Коммуникативная грамматика Решение полиномов. Корни полинома
Решение полиномов. Корни полинома Английские школы
Английские школы Логические законы
Логические законы Профессия нефтяник
Профессия нефтяник Технология двойного отжима - 2
Технология двойного отжима - 2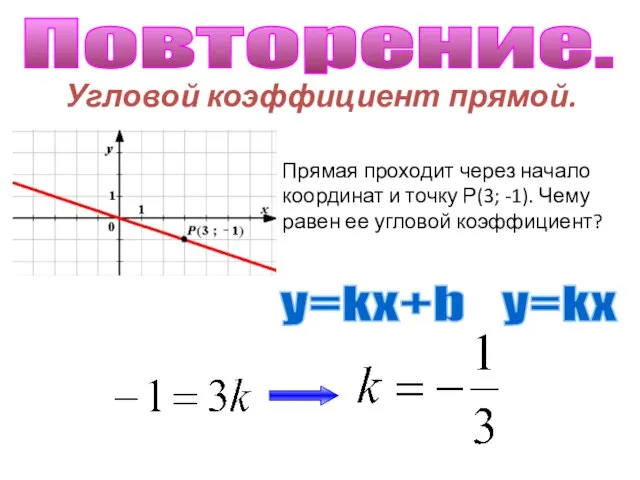 Угловой коэффициент прямой
Угловой коэффициент прямой Инновационные центры, технопаркии частно-государственное партнёрство
Инновационные центры, технопаркии частно-государственное партнёрство Aus der Geschichte der Filmkunst
Aus der Geschichte der Filmkunst Совершенствование эффективности процессов управления сбытовой деятельностью на предприятии ООО Хеленпро
Совершенствование эффективности процессов управления сбытовой деятельностью на предприятии ООО Хеленпро «Ломоносов был великий человек…» (А.С.Пушкин)
«Ломоносов был великий человек…» (А.С.Пушкин) Восторжествует ли дрбро над злом?
Восторжествует ли дрбро над злом? Современные тенденции в декорировании десертов
Современные тенденции в декорировании десертов Правила для города
Правила для города ВОЛОГДА
ВОЛОГДА Измеряем эффективностьКреативКлиентыWe Did It Конкурс рецептов от ТМ «Стожар» Месяц активности: загружено более 400 рецептов после мо
Измеряем эффективностьКреативКлиентыWe Did It Конкурс рецептов от ТМ «Стожар» Месяц активности: загружено более 400 рецептов после мо Program flow and Data collections
Program flow and Data collections Поздравление менеджерам
Поздравление менеджерам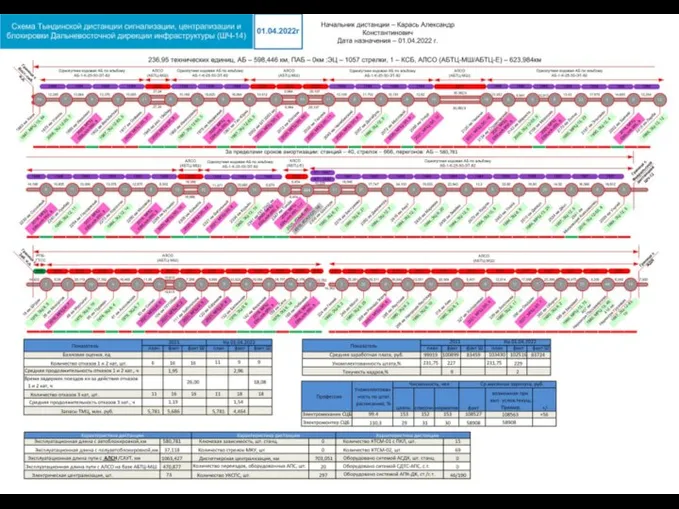 ШЧ-14 на 01 09 22
ШЧ-14 на 01 09 22 Экономика "развитого социализма" (Урок-семинар)
Экономика "развитого социализма" (Урок-семинар) Экспо (Expo) индустрияландыруд ың нышаны және техникалық
Экспо (Expo) индустрияландыруд ың нышаны және техникалық Форс-мажор в договорах оказания МТУ
Форс-мажор в договорах оказания МТУ Природа Африки
Природа Африки Чарльз Райт Миллс
Чарльз Райт Миллс Урок с экологическим содержанием по теме "Тепловые явления" 8 класс
Урок с экологическим содержанием по теме "Тепловые явления" 8 класс Иван Крамской
Иван Крамской Present Simple & Present Continuous
Present Simple & Present Continuous  Доросан. Фармакотерапевтическая характеристика.
Доросан. Фармакотерапевтическая характеристика.