Содержание
- 2. Определение функции. Среди перечисленных ниже зависимостей укажите только те, которые представляют собой функцию: у = х2
- 3. Область определения и область значений функции. Укажите область определения функций: Для функций, записанных выше, укажите область
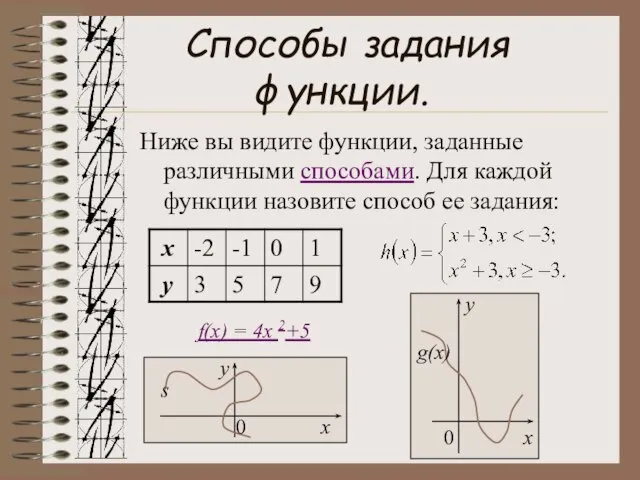
- 4. Способы задания функции. Ниже вы видите функции, заданные различными способами. Для каждой функции назовите способ ее
- 5. Виды функций. Были изучены следующие виды функций: линейная; прямая и обратная пропорциональность; дробно-линейная; квадратичная; y =
- 6. Функции у = [x], y = {x}, y= sgn x. Графики каких функций изображены на рисунках?
- 7. Выводы. Итак, в результате работы над проектом мы изучили свойства и построили графики следующих функций: линейной;
- 8. Самостоятельная работа. Самостоятельная работа состоит из двух частей: компьютерный тест; письменная работа по карточкам.
- 9. Функцией называется зависимость одной переменной от другой, при которой каждому значению независимой переменной ставится в соответствие
- 10. Существуют различные способы задания функции: аналитический; табличный; графический; кусочное задание.
- 11. Аналитический способ задания функции. Задание функции с помощью формулы (аналитического выражения) называют аналитическим способом задания функции.
- 12. Табличный способ задания функции. Функцию можно задать таблицей, где перечисляются все значения аргумента и функции. Такой
- 13. Графический способ задания функции. Задание функции с помощью графика называется графическим способом. Графиком функции у =
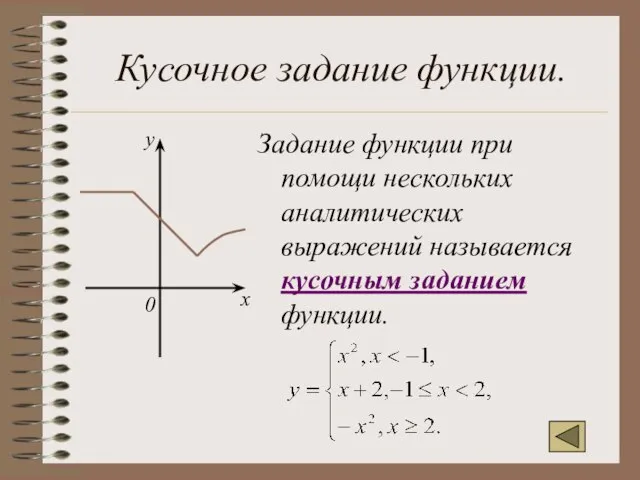
- 14. Кусочное задание функции. Задание функции при помощи нескольких аналитических выражений называется кусочным заданием функции. х у
- 15. Множество всех значений аргумента, при которых данная функция принимает числовое значение, называют областью определения этой функции.
- 16. Множество всех значений функции, которые она принимает при допустимых значениях аргумента, называют областью значений функции.
- 18. Скачать презентацию



![Функции у = [x], y = {x}, y= sgn x. Графики каких](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/349529/slide-5.jpg)









 Живая и неживая природа.
Живая и неживая природа. Занятость и безработица
Занятость и безработица Ортологическая разминка
Ортологическая разминка Стратегический анализ внешней среды организации
Стратегический анализ внешней среды организации Салонные женские стрижки
Салонные женские стрижки Пермский филиал ГУ ВШЭ Архипов Валерий Михайлович, зам. директора ПФ ГУ-ВШЭ, доцент каф.фин.менеджмента ПФ ГУ-ВШЭ. Ведерников Серге
Пермский филиал ГУ ВШЭ Архипов Валерий Михайлович, зам. директора ПФ ГУ-ВШЭ, доцент каф.фин.менеджмента ПФ ГУ-ВШЭ. Ведерников Серге Фотоэффект (11 класс)
Фотоэффект (11 класс) Что такое мастер-класс?
Что такое мастер-класс? ВЫСТУПЛЕНИЕ РУКОВОДИТЕЛЯ ГМО Белковой Елены Александровны
ВЫСТУПЛЕНИЕ РУКОВОДИТЕЛЯ ГМО Белковой Елены Александровны Выбор и обоснование выбора материала для ________________. Образец презентации по материаловедению
Выбор и обоснование выбора материала для ________________. Образец презентации по материаловедению Оценка и развитие бизнеса
Оценка и развитие бизнеса Ambient Media Что это такое? Что это такое? Ambient против классик и Ambient против классик и Эффективност ь Эффективност ь For ex. For ex. Вывод ы Вывод
Ambient Media Что это такое? Что это такое? Ambient против классик и Ambient против классик и Эффективност ь Эффективност ь For ex. For ex. Вывод ы Вывод Оценка движимого имущества. Практика решения задач
Оценка движимого имущества. Практика решения задач Разделы информатики, используемые в олимпиадных задачах
Разделы информатики, используемые в олимпиадных задачах РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК
РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК В объятьях двух морей новый
В объятьях двух морей новый Итоги 2009 – 2010 учебного года в 1 – 4 классахПедсовет 30.08 .2010г.
Итоги 2009 – 2010 учебного года в 1 – 4 классахПедсовет 30.08 .2010г.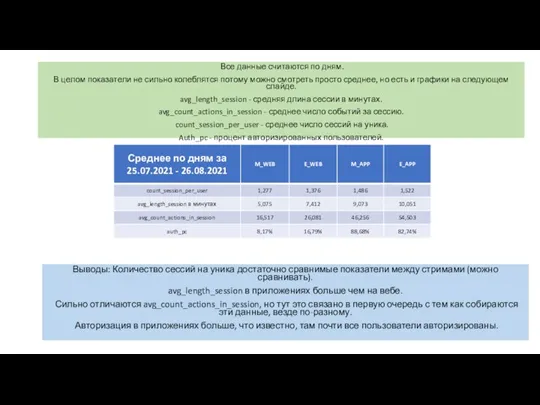 Количество сессий на уника
Количество сессий на уника Сказка о стране чисел
Сказка о стране чисел Актуальные проблемы литературы ХХ века и современной литературы
Актуальные проблемы литературы ХХ века и современной литературы Брейн-ринг Волшебные сказки
Брейн-ринг Волшебные сказки Стили в архитектуре
Стили в архитектуре O
O Мисс Филология
Мисс Филология Презентація Івкової Ольги ФГН-1,філологія, група 2
Презентація Івкової Ольги ФГН-1,філологія, група 2 Humor in advertising
Humor in advertising Презентация на тему Что мы знаем о тексте 5 класс
Презентация на тему Что мы знаем о тексте 5 класс Приготовление рабочих растворов
Приготовление рабочих растворов