Галерея числовых диковинок

В мире чисел, встречаются подлинные диковинки, редкие экземпляры, обладающие исключительными свойствами. Из таких необыкновенных чисел можно было бы составить своего рода музей числовых редкостей, настоящую «арифметическую кунсткамеру».

Число 365
365 = 10 x 10 + 11 x 11 + 12 x 12
т.е 365 равно сумме квадратов трех последовательных чисел, начиная с 10.
102 + 112 + 122 = 100 + 122 + 144 = 365
Но это еще не все, - тому же равна сумма квадратов двух следующих чисел, 13 и 14:
132 + 142 = 169 + 196 = 365

На указанном свойстве числа 365 основана задача С.А. Рачинского, изображенная на известной картине «Устный счет» Богданова-Белинского
102 + 112 + 122 + 132 + 142
365
= ?

Три Девятки
Любопытная особенность числа 999 проявляется при умножении на него другого трехзначного числа.
573 * 999 = 572 427
572=573-1 4-дополнение 5 до 9
2-дополнение 7 до 9
Решение:
573 * 999 = 573 * (1000 - 1) =
573000 -573 = 572427

Число Шехерезады
При умножении на него трехзначного числа получается результат, состоящий из самого умноженного числа, только написанного дважды.
873 x 1001 = 873873.
207 x 1001 =207207 и т. д.
Так как:
873 х 1001 = 873 х 1000 + 873 = 873000 + 873
На таких свойствах числа основаны некоторые «фокусы», в том числе и фокус Шехерезады.

Числовые пирамиды

Как объяснить своеобразные результаты умножения?
Чтобы постичь эту странную закономерность, возьмем для примера какой-нибудь из средних рядов нашей числовой пирамиды:
123456 х 9 + 7
Вместо умножения на 9 можно умножить на (10-1), т.е. приписать 0 и вычесть множимое:
123456х9+7=1234560+7-123456=
1 234 567
- 123 456
1 111 111

Пирамида 2:

Пирамида 3

Магические кольца
На каждом кольце написаны шесть цифр в одном и том же порядке, именно они образуют число 142 857.

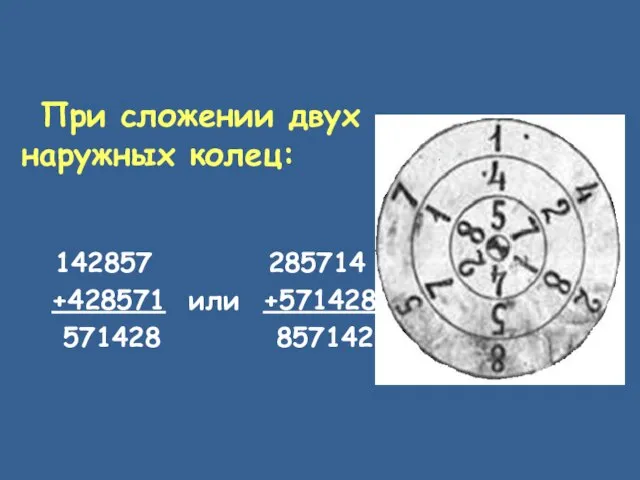
При сложении двух наружных колец:
142857 285714
+428571 или +571428
571428 857142

Тот же ряд цифр в той же последовательности получим при вычитании чисел на кольцах
428571 714285
-142857 или -142857
285714 571428

Если умножить число 142 857 на 2, на 3, на 4, на 5 или на 6, — то получим снова то же число, лишь передвинутое, в круговом порядке, на одну или несколько цифр:
142 857 * 2 = 285 714
142 857 * 3 = 428 571
142 857 * 4 = 571 428
142 857 * 5 = 714 285
142 857 * 6 = 837 142

Значит, число 142 857 не что иное, как седьмая часть 999 999 и дробь
142857 = 1
999999 7
если мы станем превращать 1/7 в десятичную дробь
1:7=0,142857 142857…