GOODNESS OF FIT

We used OLS method to develop an equation to describe the quantitative dependence between Y and X. Although the least squares method results in the line that fits the data with minimum distances, the regression equation is not a perfect predictor, unless all observed data points fall on the predicted regression line. We cannot expect all data points to fall exactly on the regression line. The regression line serves only as an approximate predictor of a Y value for a given value of X (or given values of X1, X2, …, Xk). Therefore, we need to develop a statistic that measures the variability of the actual values from the predicted Y values.
The differences between an observed Y value and the Y value predicted from the sample regression equation ( ) is called a residual.
residual for i-th observation
actual value of Y for i-th observation
estimated value of the dependent variable using regression equation (simple or multiple) for i-th observation
RESIDUALS

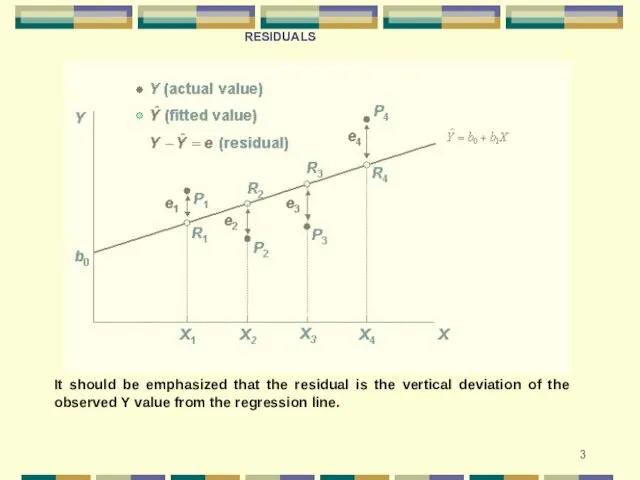
It should be emphasized that the residual is the vertical deviation of the observed Y value from the regression line.
RESIDUALS

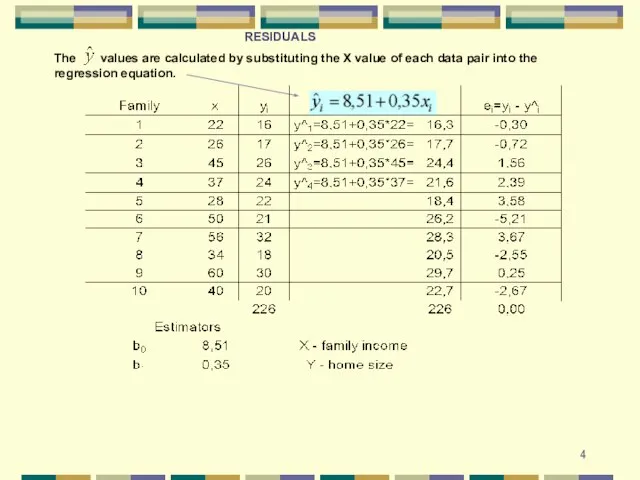
The values are calculated by substituting the X value of each data pair into the regression equation.
RESIDUALS

RESIDUALS

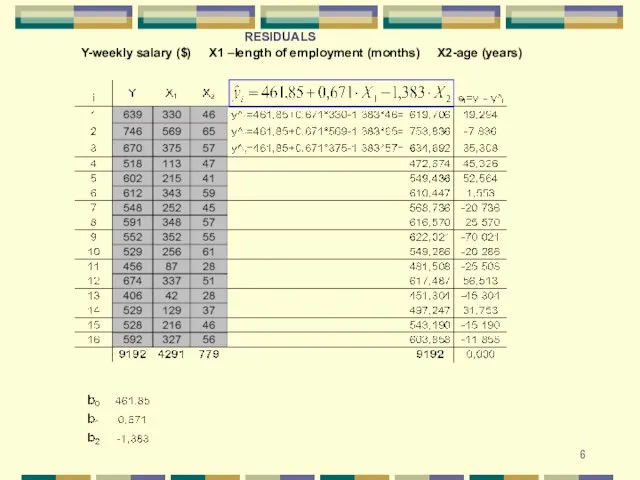
Y-weekly salary ($) X1 –length of employment (months) X2-age (years)
RESIDUALS

The residual is the vertical deviation of the observed Y value from the regression surface.
RESIDUALS

The measure of variability around the line of regression is called the standard error of the estimate (or estimation). It measures the typical difference between the actual values and the Y values predicted by the regression equation. This can be seen by the formula for the standard error of the estimate:
standard error of the estimate
sample Y values
values of Y calculated from the regression equation
sample size
number of predictors
It is measured in units of the dependent variable Y.
STANDARD ERROR OF THE ESTIMATE IS A MEASURE OF THE VARIABILITY, OR SCATTER, OF THE OBSERVED SAMPLE Y VALUES AROUND THE REGRESSION LINE.
STANDARD ERROR OF THE ESTIMATE

Let’s calculate standard error of estimation for our simple regression equation (X – family income, Y – home size. If you are lost, see slide no. 4)
STANDARD ERROR OF THE ESTIMATE

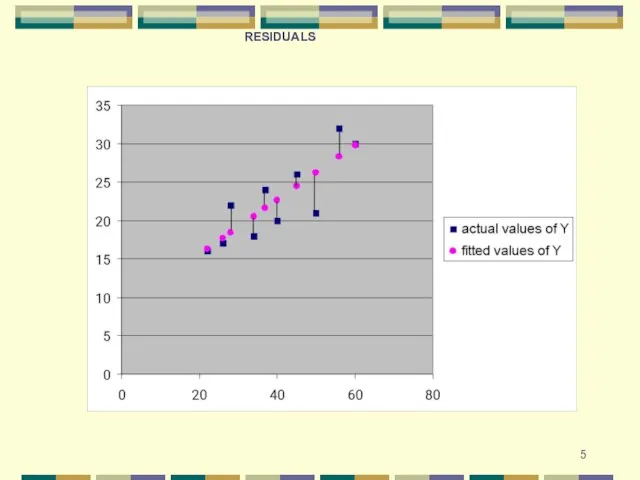
THE ACTUAL VALUES OF HOME SIZE DIFFER FROM THE ESTIMATED VALUES (USING REGRESSION EQUATION) OF HOME SIZE FOR 308 SQUARE FEET, ON AVERAGE.
What does it mean?
To answer this question, you must refer to the units in which the Y variable is measured.
Home size is measured in hundreds of square feet.
STANDARD ERROR OF THE ESTIMATE

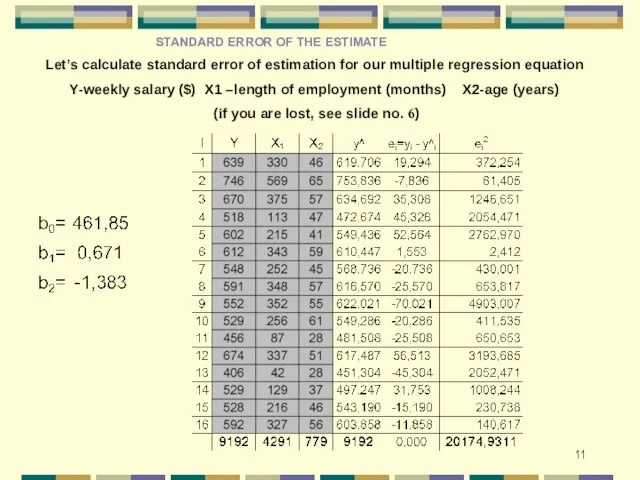
Let’s calculate standard error of estimation for our multiple regression equation
Y-weekly salary ($) X1 –length of employment (months) X2-age (years)
(if you are lost, see slide no. 6)
STANDARD ERROR OF THE ESTIMATE

What does it mean?
To answer this question, you must refer to the units in which the Y variable is measured.
THE ACTUAL VALUES OF WEEKLY SALARY DIFFER FROM THE ESTIMATED VALUES (USING REGRESSION EQUATION) FOR 39,39 $, ON AVERAGE.
THE MEAN DIFFERENCES BETWEEN THE ACTUAL AND PREDICTED VALUES OF WEEKLY SALARY ARE EQUAL 39,39 $, ON AVARAGE.
Variable Y is weekly salary. Its unit is $.
STANDARD ERROR OF THE ESTIMATE

COEFFICIENT OF RESIDUAL’S VARIABILITY
Coefficient of residual variability measures a percent of standard error of the estimate from the mean Y value. Its unit is %. We calculate it using formula:
Good model is a regression model with Ve lower than 15%.

For our examples:
COEFFICIENT OF RESIDUAL’S VARIABILITY

HOW GOOD IS OUR MODEL?
In order to examine how well the independent variable (or variables) predicts the dependent variable in our model, we need to develop several measures of variation. The first measure, the TOTAL SUM OF SQUARES (SST), is a measure of variation (or scatter) of the Y values around the mean. The total sum of squares can be subdivided into explained variation (or REGRESSION SUM OF SQUARES, SSR), that is attributable to the relationship between the independent variable (or variables) and the dependent variable, and unexplained variation (or ERROR SUM OF SQUARES, SSE), that which is attributable to factors other than the relationship between the independent variable (or variables) and the dependent variable.

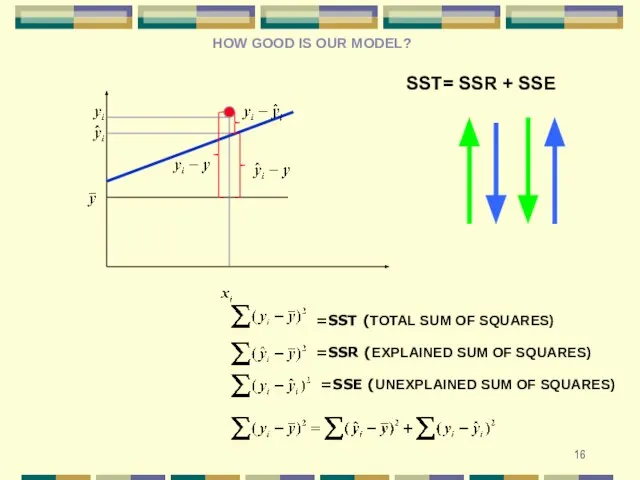
HOW GOOD IS OUR MODEL?
SST= SSR + SSE
=SST (TOTAL SUM OF SQUARES)
=SSR (EXPLAINED SUM OF SQUARES)
=SSE (UNEXPLAINED SUM OF SQUARES)

Y
Variance to be
explained by predictors
HOW GOOD IS OUR MODEL?

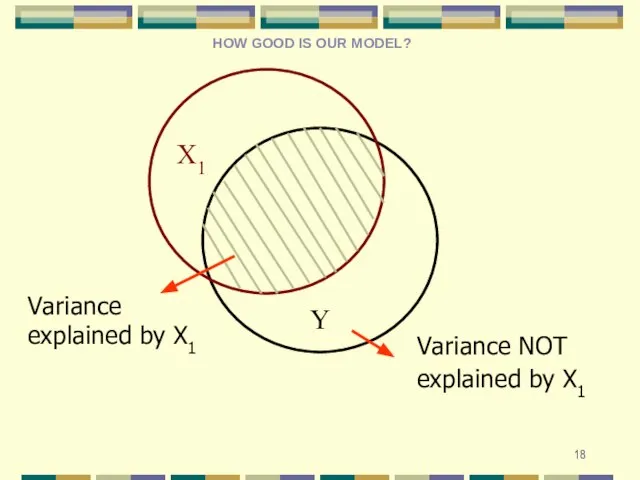
Y
X1
Variance NOT
explained by X1
Variance explained by X1
HOW GOOD IS OUR MODEL?

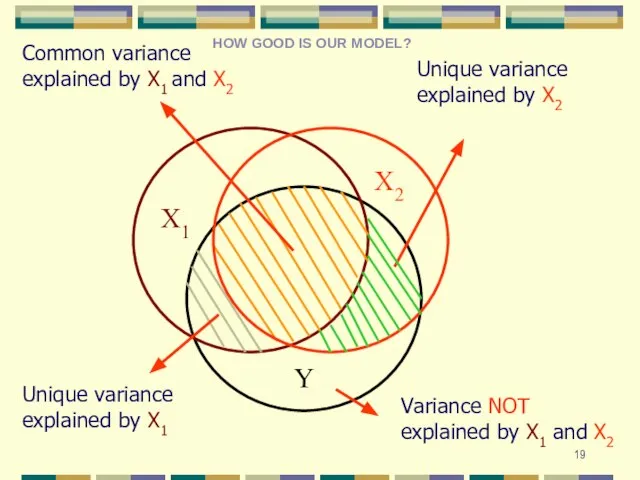
Y
X1
Variance NOT
explained by X1 and X2
Unique variance explained by X1
Unique variance explained by X2
X2
Common variance explained by X1 and X2
HOW GOOD IS OUR MODEL?

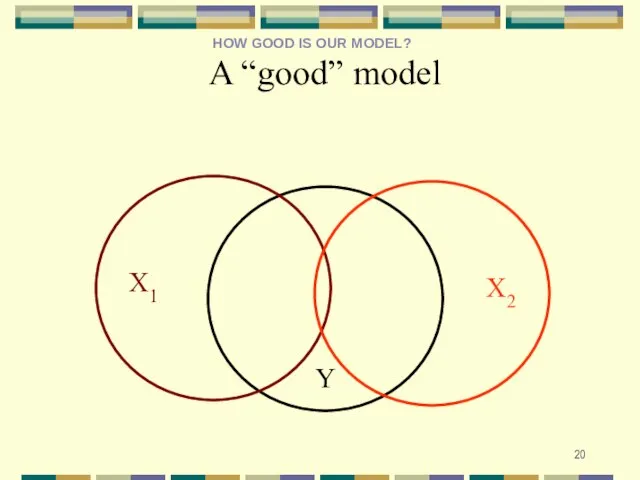
Y
X1
X2
A “good” model
HOW GOOD IS OUR MODEL?

The coefficient of determination, R2, of the fitted regression is defined as the proportion of the total sample variability explained by the regression and is
DETERMINATION COEFFICIENT
and it follows that
R2 gives the proportion of the total variation in the dependent variable explained by the independent variable (or variables).
If R2 = 1, then ???
If R2 = 0, then ???

INDETERMINATION COEFFICIENT
The coefficient of indetermination, , of the fitted regression is defined as the proportion of the total sample variability unexplained by the regression and is
and it follows that
gives the proportion of the total variation in the dependent variable unexplained by the independent variable (or variables).
If it’s equal to 1, then ???
If it’s equal to 0, then ???

ADJUSTED COEFFICIENT OF DETERMINATION
The adjusted coefficient of determination, R2, is defined as
We use this measure to correct for the fact that non-relevant independent variables will result in some small reduction in the error sum of squares. Thus the adjusted R2 provides a better comparison between multiple regression models with different numbers of independent variables. Since R2 always increases with the addition of a new variable, the adjusted R2 compensates for added explanatory variables.
or

COEFFICIENT OF MULTIPLE CORRELATION
The coefficient of multiple correlation, is the correlation between the predicted value and the observed value of the dependent variable:
and is equal to the square root of the coefficient of determination.
We use R as another measure of the strength of the linear relationship between the dependent variable and the independent variable (or variables). Thus it is comparable to the correlation between Y and X in simple regression.

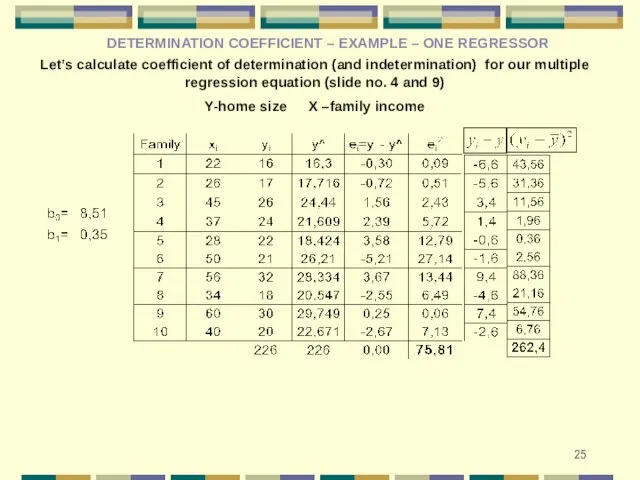
DETERMINATION COEFFICIENT – EXAMPLE – ONE REGRESSOR
Let’s calculate coefficient of determination (and indetermination) for our multiple regression equation (slide no. 4 and 9)
Y-home size X –family income

The coefficient of determination should be calculated as follows:
It’s easy to provide the coefficient of indetermination:
IT CAN BE SAID THAT 29% OF THE VARIABILITY IN HOME SIZES (Y) REMAINS UNEXPLAINED BY THE FAMILY INCOME. THEREFORE, 71% OF THE VARIABILITY IN HOME SIZES (Y) IS EXPLAINED BY THE PREDICTOR.
WE HAVE ACCOUNTED FOR 71% OF THE TOTAL VARIATION IN THE HOME SIZES BY USING INCOME AS A PREDICTOR OF HOME SIZE.
DETERMINATION COEFFICIENT – EXAMPLE – ONE REGRESSOR

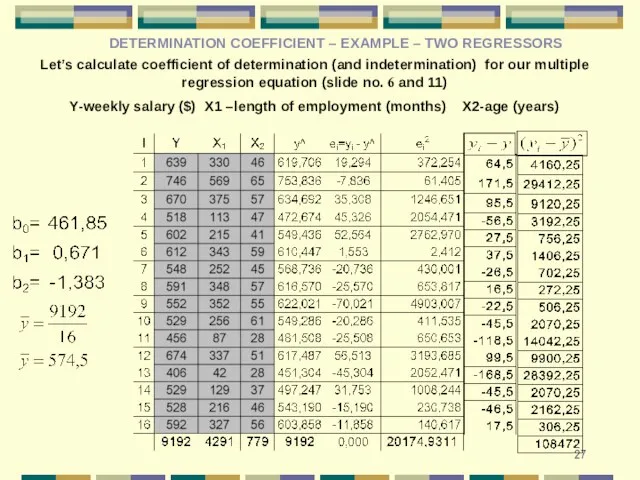
Let’s calculate coefficient of determination (and indetermination) for our multiple regression equation (slide no. 6 and 11)
Y-weekly salary ($) X1 –length of employment (months) X2-age (years)
DETERMINATION COEFFICIENT – EXAMPLE – TWO REGRESSORS

The coefficient of determination should be calculated as follows:
It’s easy to provide the coefficient of indetermination:
IT CAN BE SAID THAT 18,6% OF THE VARIABILITY IN WEEKLY SALARY (Y) REMAINS UNEXPLAINED BY LENGTH OF EMPLOYMENT (X1) AND THE AGE (X2) OF EMPLOYEES. THEREFORE, 81,4% OF THE VARIABILITY IN WEEKLY SALARY (Y) IS EXPLAINED BY THESE TWO PREDICTORS.
DETERMINATION COEFFICIENT – EXAMPLE – TWO REGRESSORS

We can compare these two models using adjusted coefficient of determination.
For regression model with one regressor (see slide 26) :
For regression model with two predictors (see slide 28):
This is better result of goodness of fit.
ADJUSTED COEFFICIENT OF DETERMINATION - EXAMPLE