Графы. Степень вершины. Подсчет числа ребер графа

Разминка…
Вставьте недостающие слова в предложения
(граф, титул, ребро, вершина)
Всем известно, что слово «граф» означает дворянский титул, например, граф Лев Николаевич Толстой. А вот в математике …
Граф – это конечная совокупность вершин,
некоторые из которых соединены ребрами.

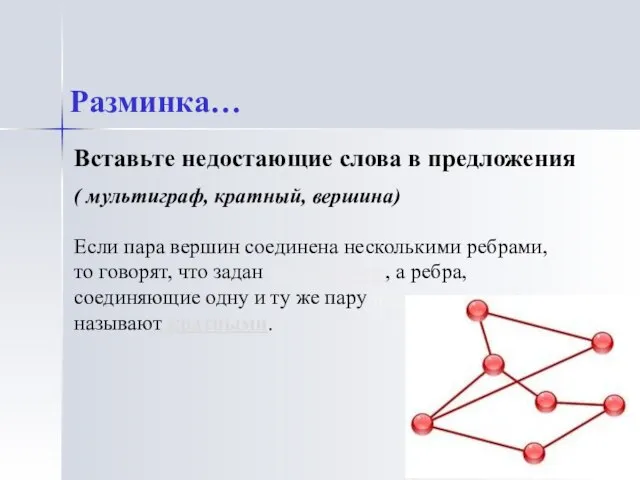
Если пара вершин соединена несколькими ребрами,
то говорят, что задан мультиграф, а ребра,
соединяющие одну и ту же пару вершин,
называют кратными.
Вставьте недостающие слова в предложения
( мультиграф, кратный, вершина)
Разминка…

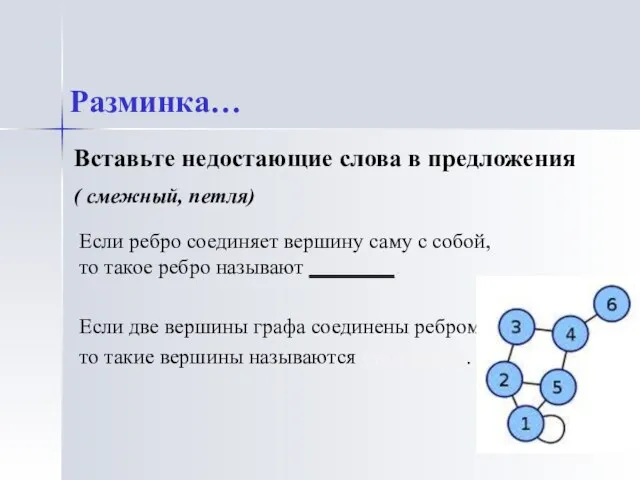
Если ребро соединяет вершину саму с собой,
то такое ребро называют ________.
Если две вершины графа соединены ребром,
то такие вершины называются смежными.
Разминка…
Вставьте недостающие слова в предложения
( смежный, петля)

В стране Знак есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9.
Путешественник обнаружил, что два города соединены дорогой в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3.
Домашняя задачка
Условие

Постройте граф, обозначив вершины графа цифрами (названия городов).
Соедините ребрами те вершины, которые удовлетворяют условию задачи.
Посчитайте количество ребер.
Можно ли долететь по воздуху из города 1 в город 9 ?
Домашняя задачка
Задания

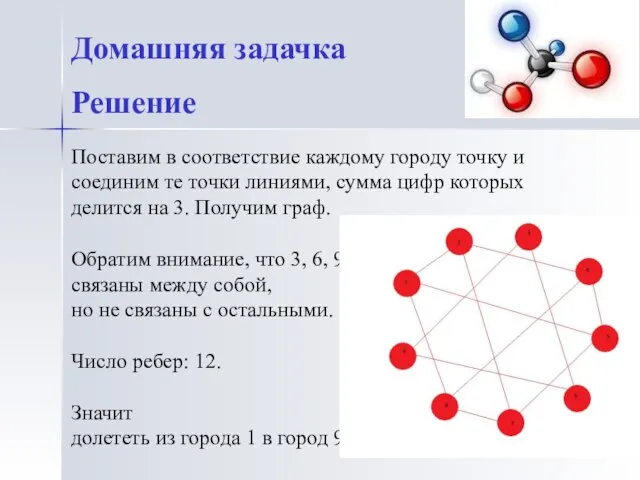
Поставим в соответствие каждому городу точку и соединим те точки линиями, сумма цифр которых делится на 3. Получим граф.
Обратим внимание, что 3, 6, 9
связаны между собой,
но не связаны с остальными.
Число ребер: 12.
Значит
долететь из города 1 в город 9 нельзя.
Домашняя задачка
Решение

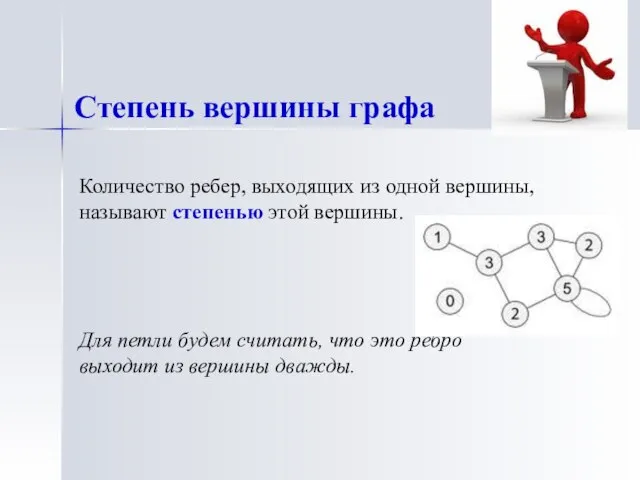
Количество ребер, выходящих из одной вершины,
называют степенью этой вершины.
Для петли будем считать, что это ребро
выходит из вершины дважды.
Степень вершины графа

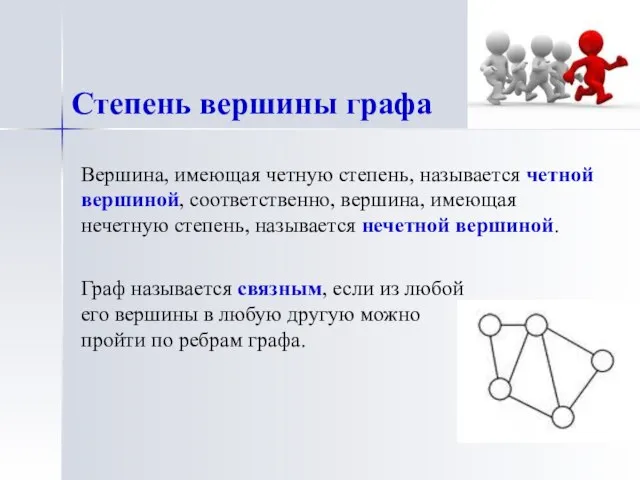
Вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
Граф называется связным, если из любой
его вершины в любую другую можно
пройти по ребрам графа.
Степень вершины графа

Количество ребер графа равно половине суммы степеней его вершин.
Пусть граф имеет n вершин, тогда число ребер равно:
Подсчет числа ребер графа

Рассмотрим утверждение о количестве ребер на примере:
Задача: в государстве 100 городов, из каждого выходит 2 дороги, кроме столицы, откуда выходит 6 дорог. Сколько всего дорог в государстве?
Решение: сложим количества дорог, выходящих из всех городов: 99*2+6=204. Это число - количество концов всех дорог. Поскольку каждая дорога имеет 2 конца, то количество дорог будет вдвое меньше, а именно 102.
Подсчет числа ребер графа

Теорема. Количество вершин нечетной степени любого графа всегда четно.
Степень вершины графа
Доказательство: Количество ребер графа равно половине суммы степеней его вершин.
Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной.
А это возможно только в том случае, если граф содержит четное число нечетных вершин.