Индивидуально-ориентированная система обучения(ИОСО)

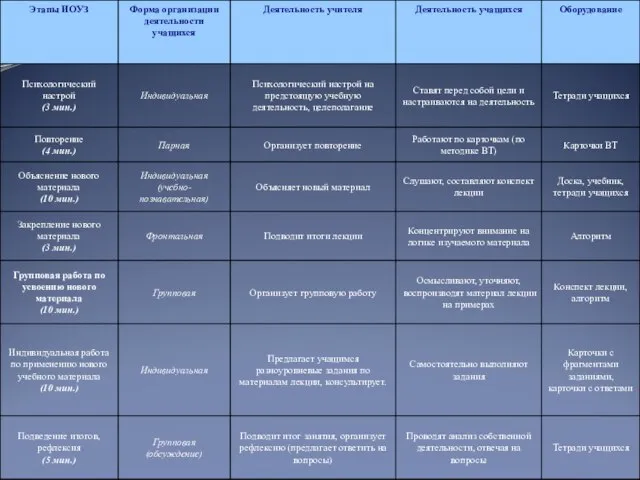
Основная идея ИОСО
Движение в своем темпе при прохождении коллективного маршрута
Выбор уровня при изучении учебного материала
Систематичность и последовательность при усвоении учебного материала

Принципы построения
Открытости
Универсальности

Календарно-тематический план (КТП)
План соответствует принципу открытости
Учтен трёхуровневый подход в организации обучения по теории Гальперина - поэтапное формирование умственных действий (понимание, усвоение, применение)

Организация учебного процесса при ИОСО
(среднее и старшее звено)
Лекционный блок (понимание нового материала)
Лабораторный блок (усвоение и применение изученного материала)
Комбинированное занятие (самостоятельное изучение нового материала)

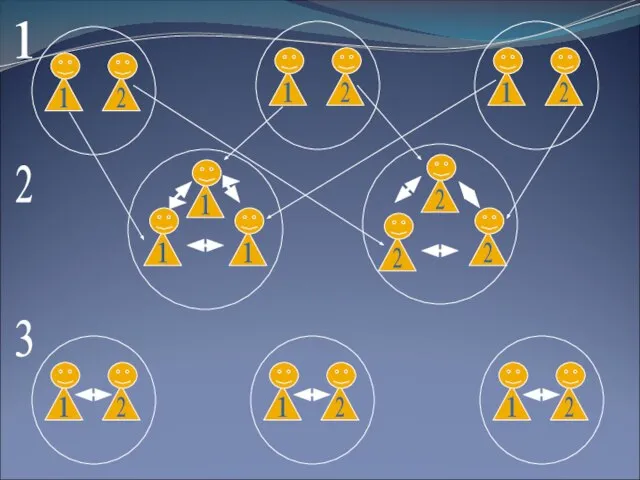
Организация учебного процесса при ИОСО (начальные классы)
I – комбинированное учебное занятие направленное на изучения нового материала
II – комбинированное учебное занятие направленное на усвоение изученного
III – комбинированное учебное занятие направленное на применение полученных знаний

Индивидуально-ориентированный учебный план по предмету (ИОУП)
Поуровневые фрагменты – задания:
Нормативный - «3» (воспроизведение и истолкование основного содержания параграфа, темы)
Компетентный - «4» (развитие у учащихся умений распознавать, действовать по алгоритму, осуществлять)
Творческий – «5» (развитие у учащихся умений решать учебные задачи с измененными условиями, исследовательских умений, творческого подхода к изучению учебного материала)

Организация выполнения ИОУП
ИОУП должны быть у каждого ученика.
Выполнение должно быть поэтапное.
Учащиеся не могут сдавать в день более, чем одну тему.
В случае пропусков занятий, учащиеся не освобождаются от отработки учебных заданий.
Учащийся сам выбирает уровень выполнения на «3», на «4», на «5».
Ребенок имеет право на пересамоопределение.
ИОП должен содержать задания минимум на 2 темы вперед.
Ребенок имеет право на опережение (кроме 1-3 классов)
Допускается пересдача. Действует правило 5 минут.

Лекционное занятие
Математика, 7 класс
Тема урока «Разложение разности квадратов на множители»
Глава V. Формулы сокращенного умножения (20 часов)
Урок № 8

План урока
Целеполагание
Работа в парах по карточкам (ВТ)
Объяснение нового материала (лекция)
Работа в группе по усвоению нового учебного материала
Индивидуальная работа по карточкам (фрагменты-задания)
ДЗ, подведение итога занятия (достиг ли своей цели? за счет чего достиг цели?).

Алгоритм применения формулы разности квадратов
Представить уменьшаемое и вычитаемое в виде квадрата одночлена (выделить квадраты одночленов);
К полученной разности квадратов применить формулу:
- в первой скобке записать разность полученных одночленов
(не меняя их порядок!),
- во второй скобке записать сумму этих же одночленов.
Например:
Разложить на множители выражение: 25а2 – 81b4
1. Сначала представим уменьшаемое и вычитаемое в виде квадрата одночлена:
25а2 = 52а2 = (5а)2; 81b4 = 92(b2)2 = (9b2)2.
Получим: 25а2 – 81b4 = (5а)2 – (9b2)2
2. К полученной разности (5а)2 – (9b2)2 применим формулу:
в первой скобке запишем разность одночленов 5а и 9b2 (не меняя их порядок) –
(5а – 9b2),
во второй скобке запишем сумму этих же одночленов – (5а + 9b2).
Окончательно получим:
25а2 – 81b4 = (5а)2 - (9b2)2 = (5а – 9b2)(5а + 9b2).

Ю.Н.Макарычев, Н.Г.Миндюк, Алгебра, 7 класс, п.34, стр.152
Пример 1. Разложим на множители выражение 36 – а2.
Так как 36 = 62, то 36 – а2 = 62 – а2 = (6 – а)(6 + а).
Пример 2. Представим в виде произведения многочлен
– 25 + х2.
Поменяем местами слагаемые. Получим выражение х2 – 25. Так как 25 = 52, то
х2 – 25 = х2 – 52 = (х – 5)(х + 5).

1
2
3

Ю.Н.Макарычев, Н.Г.Миндюк, Алгебра, 7 класс, п.34, стр.152
Пример 1. Разложим на множители выражение 36 – а2.
Так как 36 = 62, то 36 – а2 = 62 – а2 = (6 – а)(6 + а).
с2 – 91 =
Пример 2. Представим в виде произведения многочлен
– 25 + х2.
Поменяем местами слагаемые. Получим выражение х2 – 25. Так как 25 = 52, то
х2 – 25 = х2 – 52 = (х – 5)(х + 5).
– у2 + 16 =