Содержание
- 2. 1. Поняття криволінійної трапеції. 2. Площа криволінійної трапеції. Формула Ньютона-Лейбніца. 3. Визначений інтеграл. 4. Застосування визначеного
- 3. КРИВОЛІНІЙНА ТРАПЕЦІЯ Розглянемо функцію , яка є неперервною на відрізку і набуває на цьому проміжку невід'ємних
- 4. ПРИКЛАДИ КРИВОЛІНІЙНИХ ТРАПЕЦІЙ ФІГУРИ, ЩО НЕ Є КРИВОЛІНІЙНИМИ ТРАПЕЦІЯМИ Обґрунтувати чому.
- 5. ПЛОЩА КРИВОЛІНІЙНОЇ ТРАПЕЦІЇ S – площа криволінійної трапеції; F (x) – будь-яка первісна функції f(x) на
- 6. ЗАДАЧА: Знайти площу фігури, обмеженої лініями y = cos x, y = 0, x = 0,
- 7. ВИЗНАЧЕНИЙ ІНТЕГРАЛ Означення. Нехай F – первісна функції f на проміжку I, числа a і b
- 8. ІСТОРИЧНА ДОВІДКА “Розумом він перевершив рід людський ” – ці слова написані нащадками про видатного англійського
- 9. АЛГОРИТМ ЗНАХОДЖЕННЯ ІНТЕГРАЛА ЗА ФОРМУЛОЮ НЬЮТОНА-ЛЕЙБНІЦА знайти будь-яку первісну F функції f на відрізку [a; b];
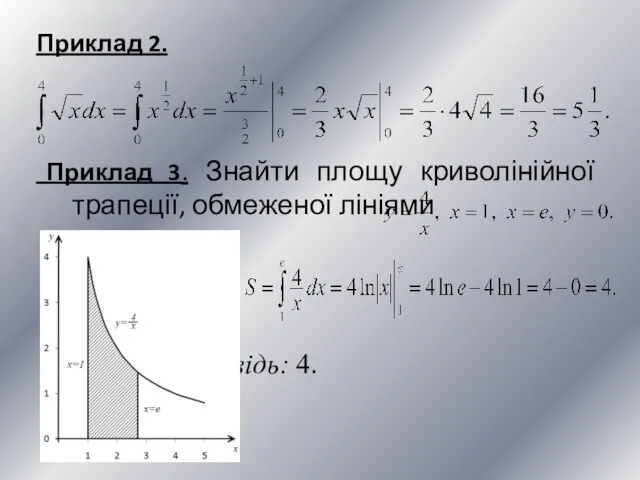
- 10. Приклад 2. Приклад 3. Знайти площу криволінійної трапеції, обмеженої лініями Відповідь: 4.
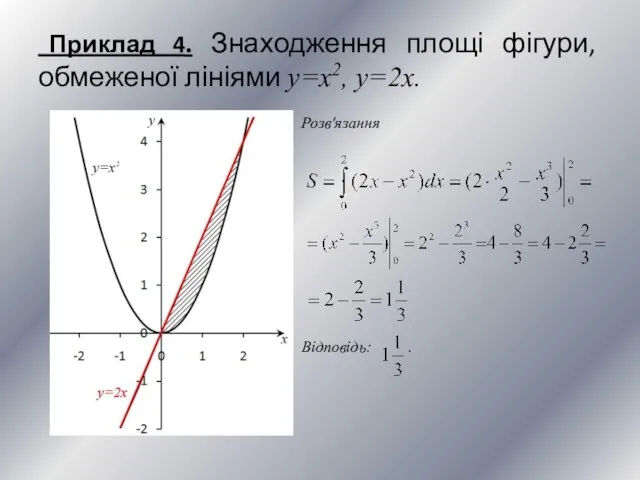
- 11. Приклад 4. Знаходження площі фігури, обмеженої лініями y=x2, y=2x. Розв'язання Відповідь: .
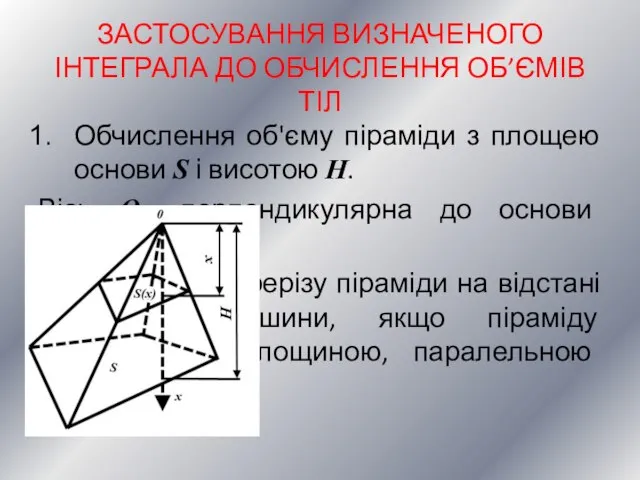
- 12. ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ДО ОБЧИСЛЕННЯ ОБ’ЄМІВ ТІЛ Обчислення об'єму піраміди з площею основи S і висотою
- 13. За властивістю площ подібних фігур:
- 14. а) кругового циліндра: S - площа основи циліндра, H – висота циліндра. ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ДО
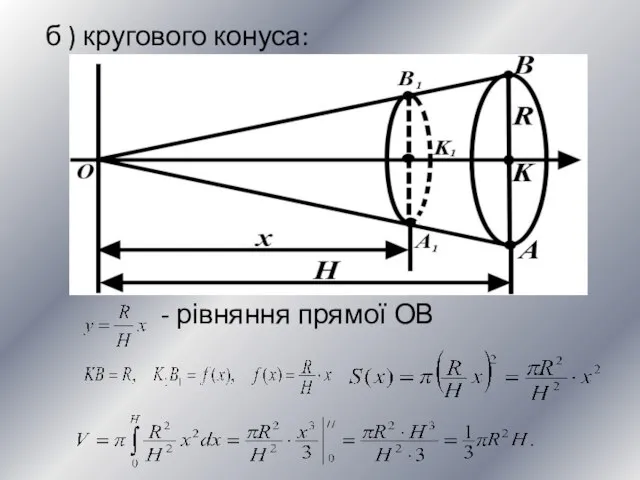
- 15. б ) кругового конуса: - рівняння прямої ОВ
- 16. Об'єм тіла, утвореного обертанням криволі-нійної трапеції, обмеженої лініями Розв'язання. Формула обчислення об'єму тіла, утвореного обертанням криволінійної
- 17. Застосування визначеного інтеграла у фізиці Обчислення шляху за відомим законом зміни швидкості. Відомо, що шлях ,
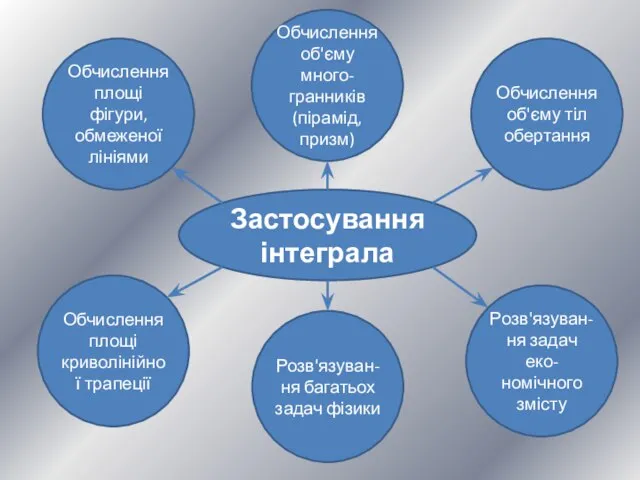
- 18. Застосування інтеграла Обчислення площі фігури, обмеженої лініями Обчислення об'єму много-гранників (пірамід, призм) Обчислення об'єму тіл обертання
- 19. Реклама Я – Інтеграл. Я все можу: обчислити і площу криволінійної трапеції, і площу фігури, обмеженої
- 20. Методичні рекомендації Слайди 2, 3 використовуються для формування поняття криволінійної трапеції Слайди 4, 5 доцільно використовувати
- 22. Скачать презентацию














 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр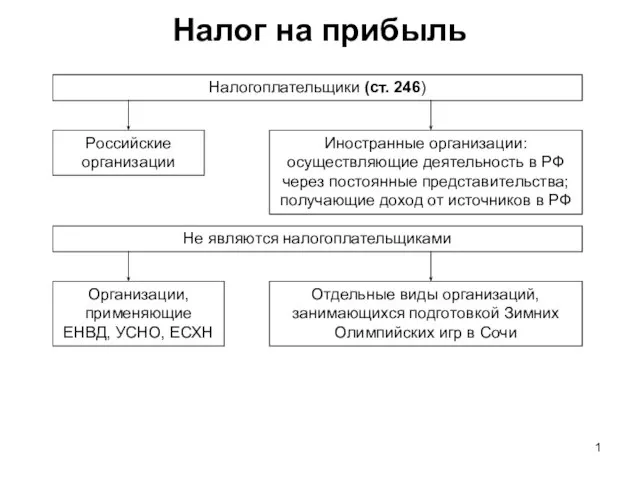 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология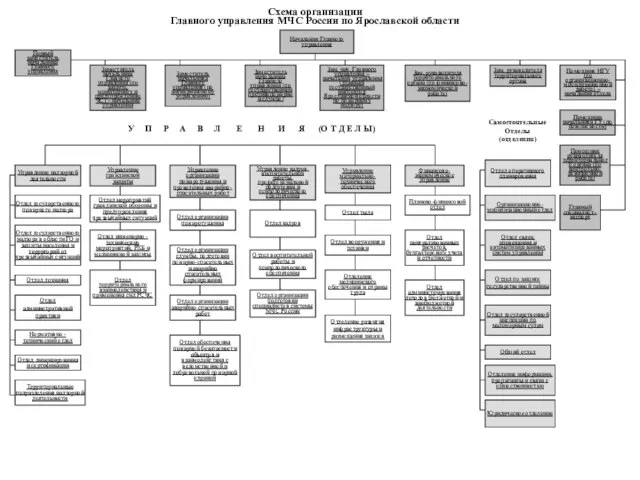 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва