Интегральное исчисление.Нахождение площадей фигур в среде Mathcad

ПЛОЩАДЬ ФИГУРЫ
Для нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом, пределы интегрирования находятся в точках пересечения заданных кривых

РАБОТА В MATHCAD
В среде Mathcad для определения пределов интегрирования используется функция root(f(x),x), а для нахождения определенного интеграла – соответствующий шаблон на наборной панели Calculus

ФОРМУЛИРОВКА ЗАДАНИЯ
Найти площадь фигуры, ограниченной кривыми:

РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Для определения пределов интегрирования необходимо будет построить графики обеих функций, графически определить приближенные значения, а потом, используя функцию root(f(x),x), найти точные значения пределов интегрирования
Для построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)

РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Зададим обе функции:

РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Построим графики этих функций:

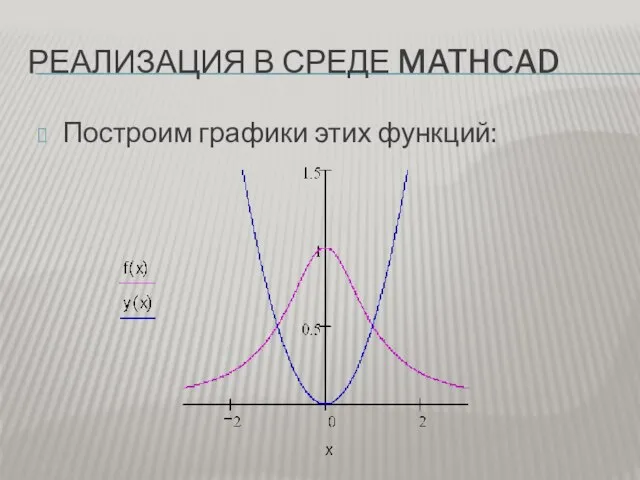
РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
По графику определилась фигура, площадь которой нужно найти:
Зададим эту новую функцию в Mathcad

РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Также графически определились приближенные пределы интегрирования
Зададим приближенное значение нижнего предела интегрирования:

РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Точное значение нижнего предела интегрирования найдем с помощью функции root.
Будем учитывать, что вместо f(x), в функции root используется g(x):

РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Зададим приближенное значение верхнего предела интегрирования и найдем его точное значение:

РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Теперь можно найти значение интеграла фигуры g(x), ограниченной линиями f(x) и y(x):