Содержание
- 2. Решение алгебраической задачи геометрическим методом. I 1)Построение геометрической модели задачи , т.е. перевод её на язык
- 3. Задача 1.Чтобы ликвидировать опоздание на 1 час , поезд на перегоне в 720км увеличил скорость ,
- 4. S1 = S2, т. .к. S1 + S2 = S3; S1 = x; S2 = 10EF,
- 5. Алгебраический метод Х (км/ч) – скорость поезда по расписанию.
- 6. Теорема Если через произвольную точку Е диагонали АС прямоугольника АВСD проведены прямые FM II AB и
- 8. Скачать презентацию
Слайд 2Решение алгебраической задачи геометрическим методом.
I
1)Построение геометрической модели задачи , т.е. перевод
Решение алгебраической задачи геометрическим методом.
I
1)Построение геометрической модели задачи , т.е. перевод

2)Решение получившейся геометрической задачи;
3)Перевод полученного ответа с геометрического языка на естественный.
II
1)При решении задачи этим методом четко определяется начало действия;
2)Графическая иллюстрация облегчает проведение анализа, составления уравнений, помогает найти несколько способов решения;
3)Расширяется область использования графиков, повышается графическая культура учеников;
4)Совершенствуется техника решения уравнений (разделений переменных);
5)Реализуются внутрипредметные (алгебра и геометрия) и межпредметные (математика и физика) связи.
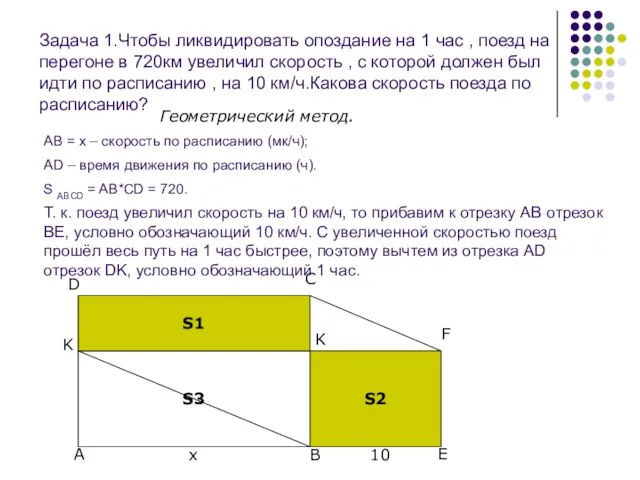
Слайд 3Задача 1.Чтобы ликвидировать опоздание на 1 час , поезд на перегоне в
Задача 1.Чтобы ликвидировать опоздание на 1 час , поезд на перегоне в
S3
S2
S1
A
B
E
x
10
K
D
C
F
Геометрический метод.
K
АВ = х – скорость по расписанию (мк/ч);
AD – время движения по расписанию (ч).
S ABCD = AB*CD = 720.
Т. к. поезд увеличил скорость на 10 км/ч, то прибавим к отрезку АВ отрезок ВЕ, условно обозначающий 10 км/ч. С увеличенной скоростью поезд прошёл весь путь на 1 час быстрее, поэтому вычтем из отрезка AD отрезок DK, условно обозначающий 1 час.
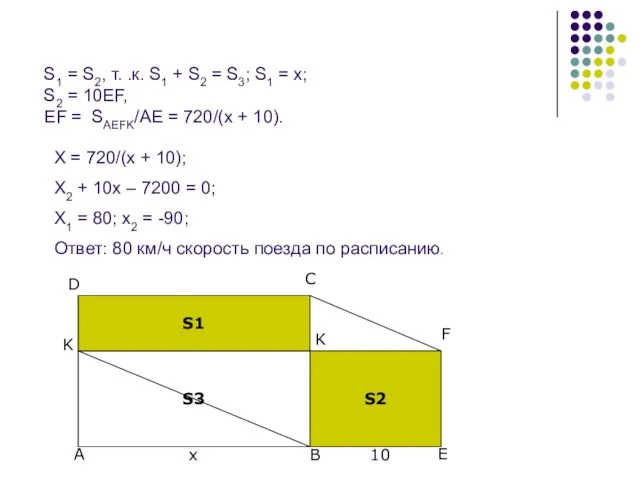
Слайд 4S1 = S2, т. .к. S1 + S2 = S3; S1 =
S1 = S2, т. .к. S1 + S2 = S3; S1 =
S3
S2
S1
A
B
E
x
10
K
D
C
F
K
Х = 720/(х + 10);
Х2 + 10х – 7200 = 0;
Х1 = 80; х2 = -90;
Ответ: 80 км/ч скорость поезда по расписанию.
Слайд 5 Алгебраический метод
Х (км/ч) – скорость
поезда
по расписанию.
Алгебраический метод
Х (км/ч) – скорость
поезда
по расписанию.

Слайд 6 Теорема
Если через произвольную точку Е диагонали АС прямоугольника АВСD проведены прямые
Теорема
Если через произвольную точку Е диагонали АС прямоугольника АВСD проведены прямые
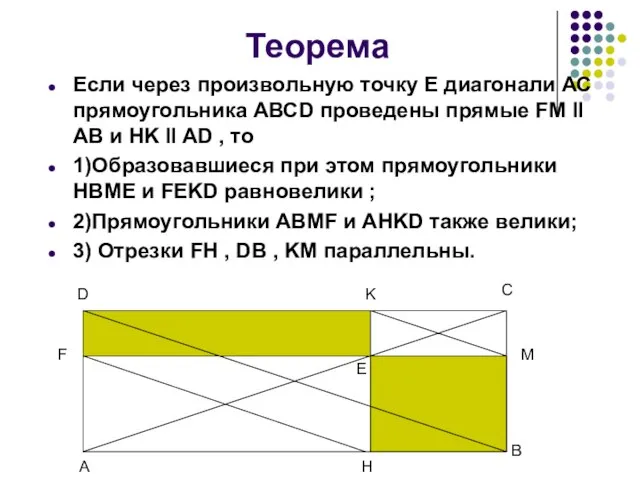
1)Образовавшиеся при этом прямоугольники HBME и FEKD равновелики ;
2)Прямоугольники ABMF и AHKD также велики;
3) Отрезки FH , DB , KM параллельны.
D
K
C
M
B
H
A
F
E
 Всё о профессии ХИРУРГА
Всё о профессии ХИРУРГА Стабилизационный фонд РФ
Стабилизационный фонд РФ Русская трапеза
Русская трапеза Star Hour
Star Hour Бизнес-план антикафе Час за минуту
Бизнес-план антикафе Час за минуту Разработка алгоритмов
Разработка алгоритмов  Урок истории в 5 классе по теме: «Поход Александра Македонского на восток»
Урок истории в 5 классе по теме: «Поход Александра Македонского на восток» Жанры изобразительного искусства
Жанры изобразительного искусства Подготовка к ЕГЭ (задание В7).» Презентация по математике для урока по теме: «Нахождение значения выражения
Подготовка к ЕГЭ (задание В7).» Презентация по математике для урока по теме: «Нахождение значения выражения Терморегуляторы. Комплект для управления снеготаянием
Терморегуляторы. Комплект для управления снеготаянием Федеральная миграционнная служба
Федеральная миграционнная служба Цветковые растения
Цветковые растения  Технология формирования диагностических навыков у обучающихся
Технология формирования диагностических навыков у обучающихся ОСЕВАЯ И ЦЕНТРАЛЬНАЯ Симметрии
ОСЕВАЯ И ЦЕНТРАЛЬНАЯ Симметрии Подведение итогов
Подведение итогов Золотые правила питания
Золотые правила питания Нижний Новгород 15 февраля 2012 г.
Нижний Новгород 15 февраля 2012 г. Лист — боковой орган побега
Лист — боковой орган побега Слагаемые успеха
Слагаемые успеха Поделки из вторсырья
Поделки из вторсырья Исследование демографической ситуации села Бала Верхоянского района Республики Саха (Якутия) по половозрастному составу
Исследование демографической ситуации села Бала Верхоянского района Республики Саха (Якутия) по половозрастному составу У истоков русской журналистики и журналистского образования в Санкт-Петербургском государственном университете
У истоков русской журналистики и журналистского образования в Санкт-Петербургском государственном университете Литературный турнир по произведениям русских писателей 20 века
Литературный турнир по произведениям русских писателей 20 века ПРЕЗЕНТАЦИЯ на QS-форуме КООМЕТ СИСТЕМЫ МЕНЕДЖМЕНТА КАЧЕСТВА ВНИИФТРИ
ПРЕЗЕНТАЦИЯ на QS-форуме КООМЕТ СИСТЕМЫ МЕНЕДЖМЕНТА КАЧЕСТВА ВНИИФТРИ Кадровый состав. В школе работает 24 педагога До 5 летОт 5 до10летОт10-15летБолее15лет 40119 Имеют категории высшуюпервуювторуюНе имеют ка
Кадровый состав. В школе работает 24 педагога До 5 летОт 5 до10летОт10-15летБолее15лет 40119 Имеют категории высшуюпервуювторуюНе имеют ка Путешествие на поезде «Здоровье» - презентация для начальной школы
Путешествие на поезде «Здоровье» - презентация для начальной школы Презентация на тему Хлеб - драгоценность
Презентация на тему Хлеб - драгоценность Особенности скелета человека связанные с прямохождением и трудовой деятельностью
Особенности скелета человека связанные с прямохождением и трудовой деятельностью