Содержание
- 2. Фотография здания, высоту которого я измерял.
- 3. Цель работы: Измерение высоты школьного здания. «Время от времени следует производить самые дикие эксперименты. Из них
- 4. І способ: Встанем перед школой в полдень (чем лучше будет определён момент полудня, тем точнее окажется
- 5. І І способ: Начнем эксперимент ровно в полдень. Измерения лучше проводить в самый длительный световой день,
- 6. І І І способ: Прикрепим к нити с одного конца груз и закинем нить так, чтобы
- 7. І V способ: Установим рейку перпендикулярно земле на расстоянии S от стены школы. Глаз наблюдателя расположим
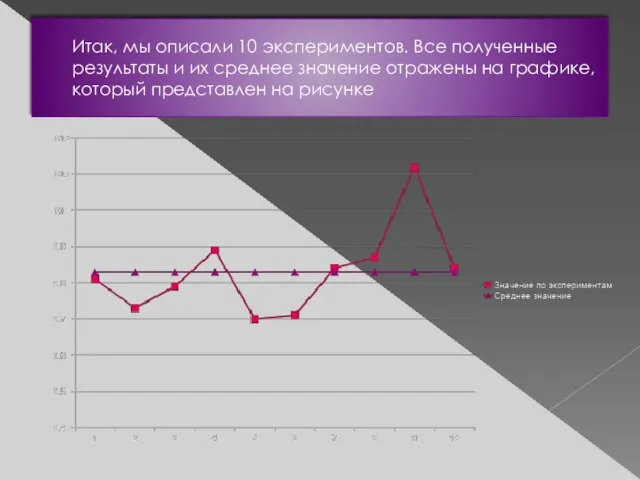
- 8. Итак, мы описали 10 экспериментов. Все полученные результаты и их среднее значение отражены на графике, который
- 9. ПОГРЕШНОСТЬ Найдём относительную погрешность: Где Hср – среднее значение высоты школы, а H max и H
- 11. Скачать презентацию







 Контрольний норматив. Тести і нормативи оцінки фізичної підготовленості студентів
Контрольний норматив. Тести і нормативи оцінки фізичної підготовленості студентів Inventions. Text provided by ukurcheev bogdan
Inventions. Text provided by ukurcheev bogdan Подходы к управлению
Подходы к управлению Колледж бодибилдеров
Колледж бодибилдеров Географические координаты
Географические координаты Презентация на тему Частушки
Презентация на тему Частушки СКАЗКА
СКАЗКА Проект «Первая помощь при переломах, вывихах и растяжении связок»
Проект «Первая помощь при переломах, вывихах и растяжении связок» Виртуальные машины
Виртуальные машины Презентация на тему "Формирование учебной мотивации у младших школьников" - скачать презентации по Педагогике
Презентация на тему "Формирование учебной мотивации у младших школьников" - скачать презентации по Педагогике Профессиональный клуб учителей
Профессиональный клуб учителей Сувенирная мастерская, 2 год обучения
Сувенирная мастерская, 2 год обучения БГТУ ВОЕНМЕХ им. Д.Ф. Устинова
БГТУ ВОЕНМЕХ им. Д.Ф. Устинова Пророки
Пророки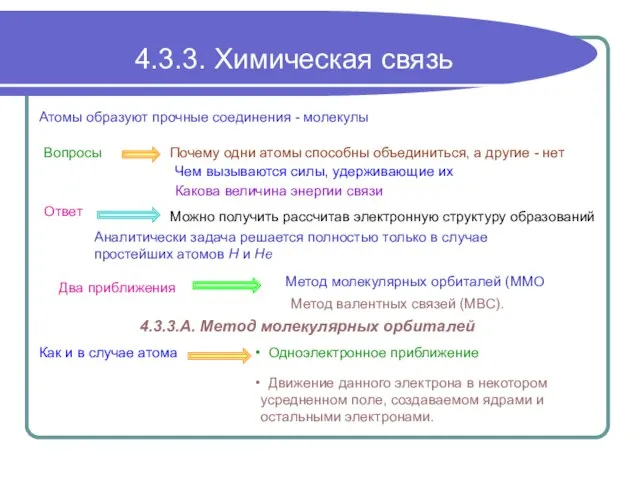 4.3.3. Химическая связь
4.3.3. Химическая связь Тема урока:Сделки и представительство.
Тема урока:Сделки и представительство. Мои пробабушка и продедушка
Мои пробабушка и продедушка Презентация на тему Изобразительное искусство классицизма и рококо
Презентация на тему Изобразительное искусство классицизма и рококо Проектирование блочной котельной
Проектирование блочной котельной Презентация на тему Характеристика стран ОПЕК
Презентация на тему Характеристика стран ОПЕК  Тренинг-семинар Твой характер – в твоих руках
Тренинг-семинар Твой характер – в твоих руках Мастер-класс Цветочное панно
Мастер-класс Цветочное панно Мастер-класс на тему: Мозаика из яичной скорлупы
Мастер-класс на тему: Мозаика из яичной скорлупы Соматоформды бұзылыстар
Соматоформды бұзылыстар Взаимодействие аллельных генов. Кодомирование
Взаимодействие аллельных генов. Кодомирование День Святого Валентина
День Святого Валентина IT-лицей Казанского федерального университета
IT-лицей Казанского федерального университета ПЕРИОДЫ ДЕТСКОГО ВОЗРАСТА. ЗНАЧЕНИЕ ГЕНЕТИЧЕСКИХ И НАСЛЕДСТВЕННЫХ факторов
ПЕРИОДЫ ДЕТСКОГО ВОЗРАСТА. ЗНАЧЕНИЕ ГЕНЕТИЧЕСКИХ И НАСЛЕДСТВЕННЫХ факторов