Содержание
- 2. Актуальность
- 3. Используемые определения Конфигурация - магнитное состояние системы спинов, которое характеризуется уникальным распределением магнитных моментов по направлениям
- 4. Используемые определения Спиновое стекло - магнитная фаза, в которую магнетик переходит ниже определённой критической температуры (температура
- 5. Совокупность элементов, по которым происходит протекание, называется перколяционным кластером. Будучи по своей природе связным случайным графом,
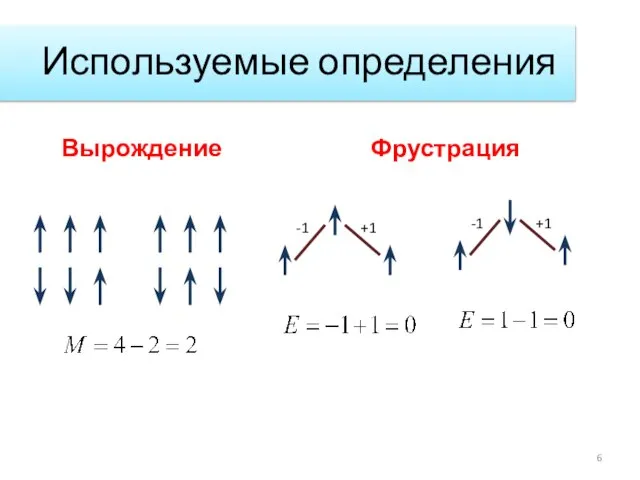
- 6. Используемые определения Фрустрация Вырождение
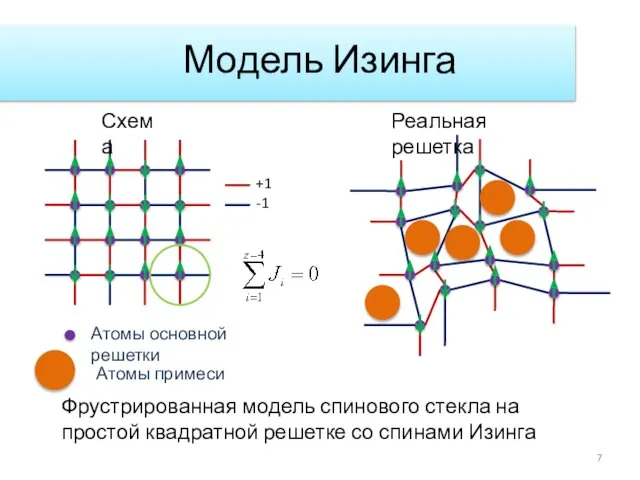
- 7. Модель Изинга +1 -1 Фрустрированная модель спинового стекла на простой квадратной решетке со спинами Изинга Схема
- 8. Модель Изинга Система описывается с помощью функционала энергии, называющегося гамильтонианом, который ассоциирует каждую уникальную конфигурацию системы
- 9. Модель Изинга При этом вероятность любой из возможных конфигураций задается распределением Гиббса. В нашей модели каждый
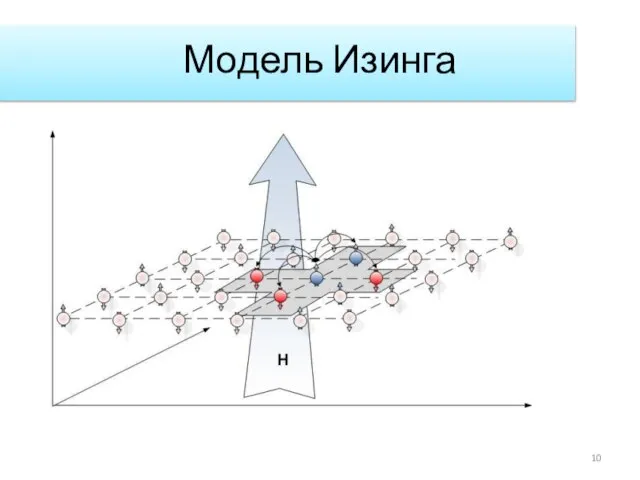
- 10. Модель Изинга
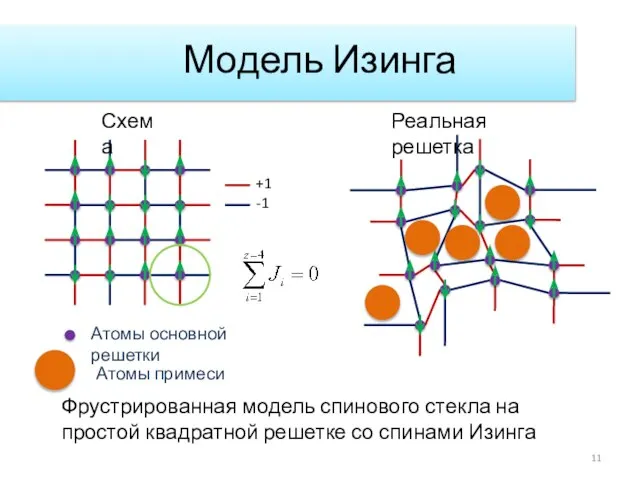
- 11. Модель Изинга +1 -1 Фрустрированная модель спинового стекла на простой квадратной решетке со спинами Изинга Схема
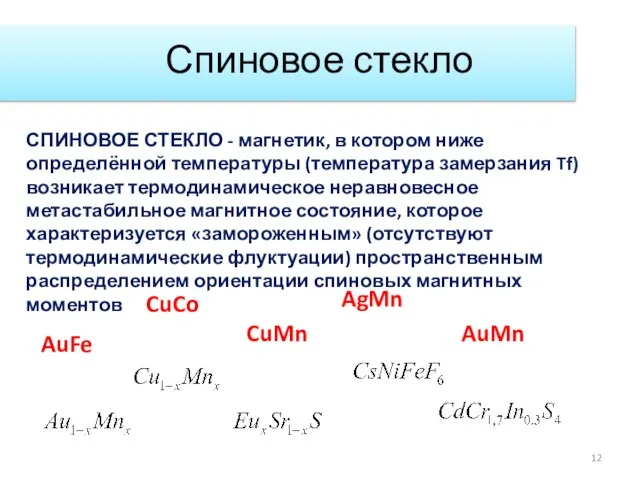
- 12. Спиновое стекло СПИНОВОЕ СТЕКЛО - магнетик, в котором ниже определённой температуры (температура замерзания Tf)возникает термодинамическое неравновесное
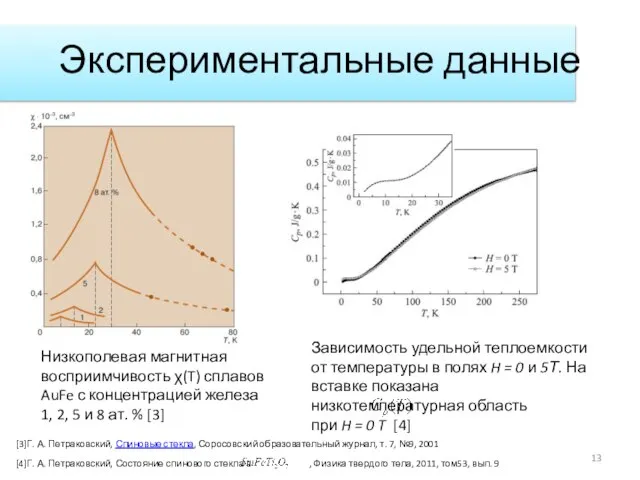
- 13. Экспериментальные данные Низкополевая магнитная восприимчивость χ(T) сплавов AuFe с концентрацией железа 1, 2, 5 и 8
- 14. Алгоритм Разработан программный инструментарий для моделирования динамики физических величин, характеризующих систему с заданным (в т.ч. знакопеременным)
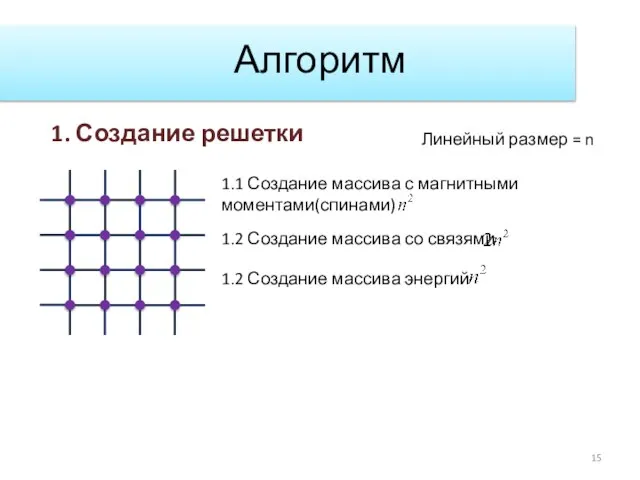
- 15. Алгоритм 1. Создание решетки 1.1 Создание массива с магнитными моментами(спинами) 1.2 Создание массива со связями 1.2
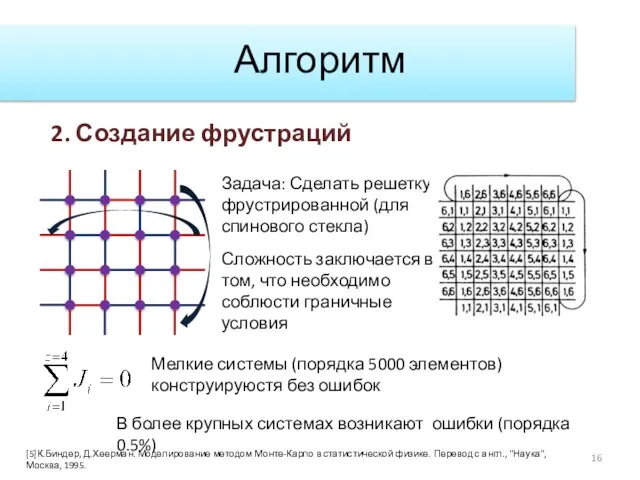
- 16. Алгоритм 2. Создание фрустраций Задача: Сделать решетку фрустрированной (для спинового стекла) Сложность заключается в том, что
- 17. Алгоритм 3. Монте-Карло При моделировании возможно задать количество Монте-Карло проходов Каждый Монте-Карло проход состоит: 1.Случайным образом
- 18. Алгоритм 4. Расчет параметра порядка Для разделения парамагнитной и спинстекольной фаз предлагается использовать параметр «порядка», который
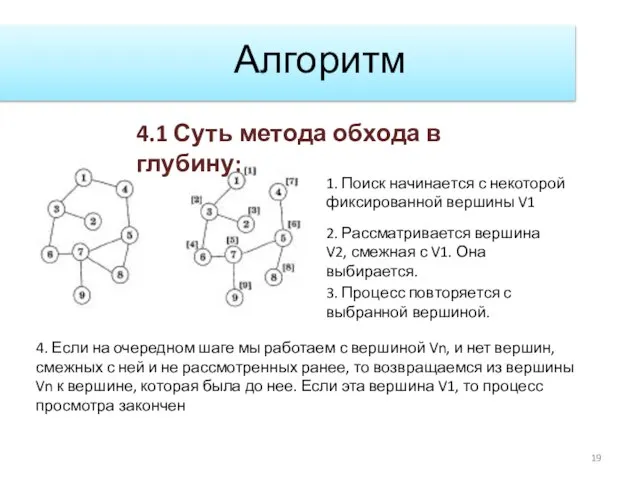
- 19. Алгоритм 4.1 Суть метода обхода в глубину: 2. Рассматривается вершина V2, смежная с V1. Она выбирается.
- 20. Алгоритм 4.2 Суть метода обхода в ширину: Такой порядок обхода обеспечивается благодаря тому, что создается очередь.
- 21. Алгоритм 5.Подсчет намагниченности, энергии. Вывод. Намагниченность считается простым суммированием всех спинов. Общая энергия считается суммированием всех
- 22. Результаты Ферромагнетик 2D ПК 4 соcеда Подпись указать -4, М, (-4)+(-2), число МК проходов, размер системы,
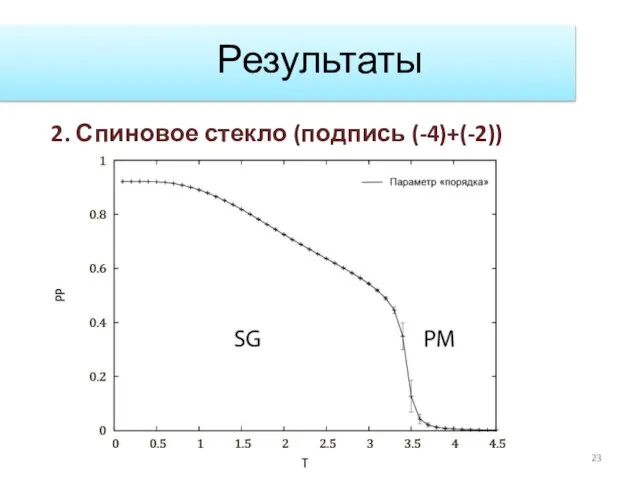
- 23. Результаты 2. Спиновое стекло (подпись (-4)+(-2))
- 24. Зависимость пп от числа проходов МК
- 25. Cверхмасшабирование и дальнейшее развитие исследований Будет проведено распараллеливание алгоритма с целью увеличения числа частиц в системе
- 26. Выводы Разработан алгоритм, написана программа ЭВМ на языке С#. Проведены численные эксперименты моделирующие поведение ферромагнетика, и
- 27. Заключение Закон температурного спада предлагаемого параметра «порядка» (-4) для ферромагнитной фазы совпадает с законом температурного поведения
- 29. Скачать презентацию
















 С ЧЕГО НАЧИНАЕТСЯ МОДЕРНИЗАЦИЯ?
С ЧЕГО НАЧИНАЕТСЯ МОДЕРНИЗАЦИЯ? Азбука потребителя
Азбука потребителя История лоскутного шитья
История лоскутного шитья Проект «Вековая история. Наша школа». Данный проект относится к предметной области окружающий мир. Участники проекта: обучающиес
Проект «Вековая история. Наша школа». Данный проект относится к предметной области окружающий мир. Участники проекта: обучающиес Учет и анализ в системе управления персоналом организации
Учет и анализ в системе управления персоналом организации Цивилизационный (духовно-культурный) подход к праву
Цивилизационный (духовно-культурный) подход к праву Олимпизм и воспитание
Олимпизм и воспитание Все профессии важны ! Все профессии нужны
Все профессии важны ! Все профессии нужны Презентация на тему ПЛАН работы РМО учителей математики на 2015-2017 год
Презентация на тему ПЛАН работы РМО учителей математики на 2015-2017 год Разработка урока по физике
Разработка урока по физике Аргументация в рекламе
Аргументация в рекламе Чем отличается Дед Мороз от Санта Клауса
Чем отличается Дед Мороз от Санта Клауса Home door. Люкс 1а медный антик/венге №32
Home door. Люкс 1а медный антик/венге №32 Сандро Боттичелли (1475-1510)
Сандро Боттичелли (1475-1510) Закрепление изученного
Закрепление изученного Проектирование бизнеса. Формы организации бизнеса и организационная структура
Проектирование бизнеса. Формы организации бизнеса и организационная структура Особова справа Белоуса Б.Г
Особова справа Белоуса Б.Г Jeu de société (les verbes)
Jeu de société (les verbes) Технические требования. Лист4
Технические требования. Лист4 Новая модель цивилизации
Новая модель цивилизации Открытие локального производства в России Реваз Хетагури Менеджер по операционной деятельности, Cisco Валерия Кашибадзе Менеджер
Открытие локального производства в России Реваз Хетагури Менеджер по операционной деятельности, Cisco Валерия Кашибадзе Менеджер  Натюрморт
Натюрморт Мы изучаем - баскетбол
Мы изучаем - баскетбол Н. В. Гоголь в разделе «Что такое слово и словесность» пишет: "Говорится все, записывается немногое, и только то, что нужно. Отсюда зн
Н. В. Гоголь в разделе «Что такое слово и словесность» пишет: "Говорится все, записывается немногое, и только то, что нужно. Отсюда зн Банкетные ведущие Свои
Банкетные ведущие Свои 5 Почему нужно быть терпимыми
5 Почему нужно быть терпимыми Председатель Комитета по транспортно-транзитной политике Н.А.Асаул Заседание Правительства Санкт-Петербурга 21 июля 2009 года Об отр
Председатель Комитета по транспортно-транзитной политике Н.А.Асаул Заседание Правительства Санкт-Петербурга 21 июля 2009 года Об отр «Россия должна стать самой привлекательной для жизни страной. Путь развития к 2020 году определен – это инновации: он связан, прежде
«Россия должна стать самой привлекательной для жизни страной. Путь развития к 2020 году определен – это инновации: он связан, прежде