Комбинаторные задачи (5 класс)

Рассмотреть решение комбинаторных задач, которые включены в учебник В. Я. Виленкина
« Математика», 5 класс, расширить знания .

Что такое комбинаторика?
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи,называется комбинаторикой.
« Комбинаторика»( лат. «combinare», соединять, сочетать)

Займёмся делом!
Задача 11. Запишите все трёхзначные числа, для записи которых употребляются только цифры 1,2.
Решение В записи числа на первом месте ( в разряде сотен) может стоять цифра 1 или цифра 2:

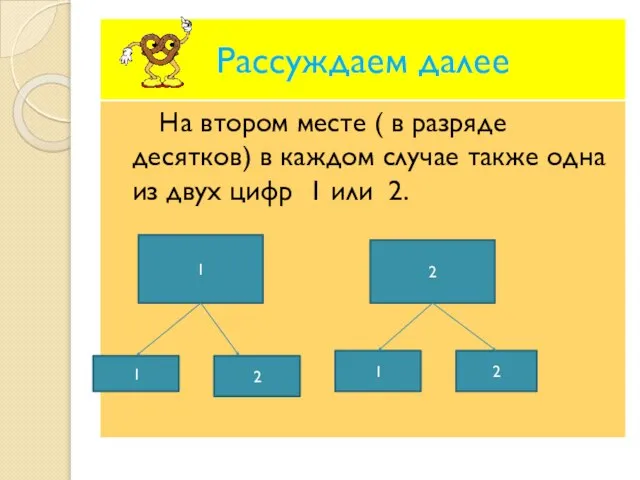
Рассуждаем далее
На втором месте ( в разряде десятков) в каждом случае также одна из двух цифр 1 или 2.
1
2
1
2
1
2

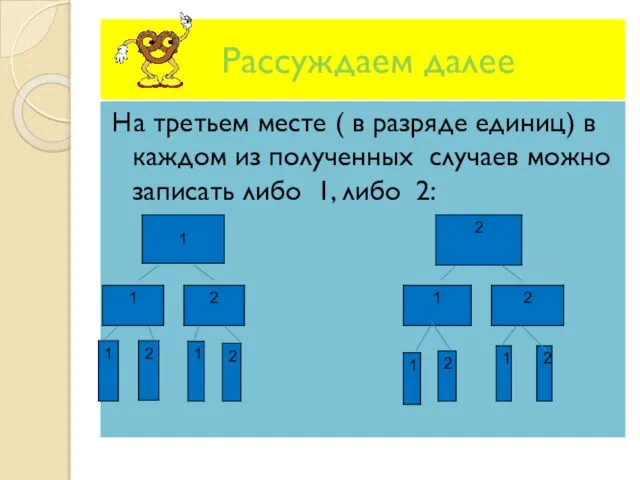
Рассуждаем далее
На третьем месте ( в разряде единиц) в каждом из полученных случаев можно записать либо 1, либо 2:

Вывод:
В итоге мы видим, что получилось восемь чисел: 111,112,121,122,211,212,221,222
Задача12 . Запишите все трёхзначные числа, для записи которых употребляются числа 0,7.

Задача №96
Решение. Президентом фирмы можно избрать одного из 5 человек. После того как президент избран, вице- президентом можно выбрать любого из четырёх оставшихся членов правления.
1
2
3
4
5
2
3
4
5
1
3
4
5
1
2
4
5
1
2
3
5
1
2
3
4
Значит выбрать президента можно пятью способами, и для каждого выбранного президента четырьмя способами можно выбрать вице- президента. Следовательно , общее число способов выбрать президента и вице- президента фирмы равно 5*4=20

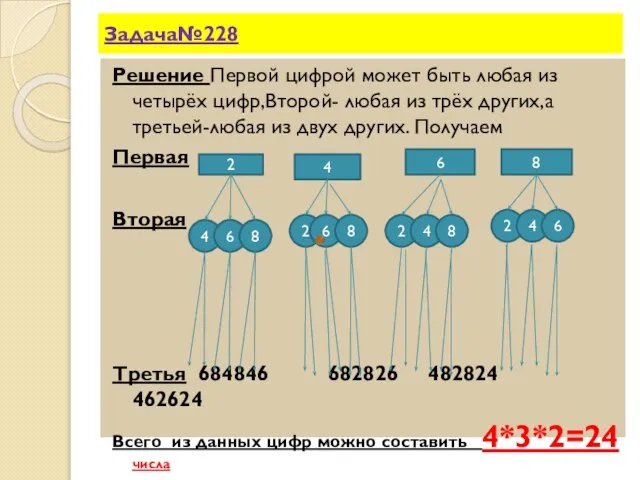
Задача№228
Решение Первой цифрой может быть любая из четырёх цифр,Второй- любая из трёх других,а третьей-любая из двух других. Получаем
Первая
Вторая
Третья 684846 682826 482824 462624
Всего из данных цифр можно составить 4*3*2=24 числа
2
4
6
8
4
6
8
2
6
8
2
4
8
2
4
6

Можно заглянуть в будущее!
Размещением из n элементов по k (k любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов. n!
Подсмотрим формулу An = -------
( n-k)!
В задаче№228,где надо найти количество трёхзначных чисел, которые можно составить из цифр 3,4,6,8,как раз и надо число размещений из 4 элементов по 3.
4! 1*2*3*4
Ищем A4 =----- =-------------= 24 УРА!
(4-3)! 1
k
3

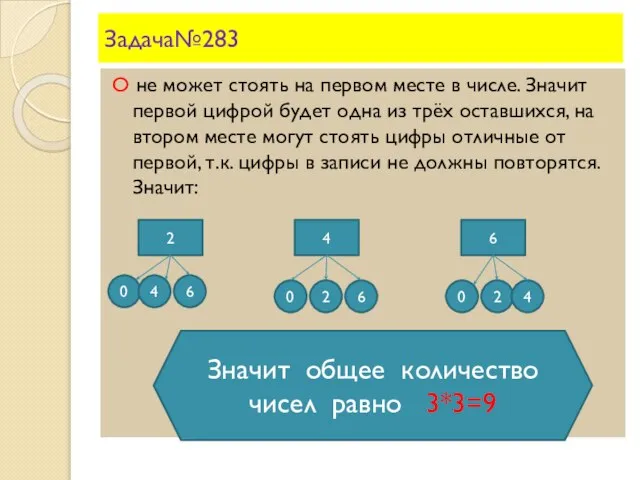
Задача№283
О не может стоять на первом месте в числе. Значит первой цифрой будет одна из трёх оставшихся, на втором месте могут стоять цифры отличные от первой, т.к. цифры в записи не должны повторятся. Значит:
2
4
6
0
4
6
0
2
6
0
2
4
Значит общее количество чисел равно 3*3=9

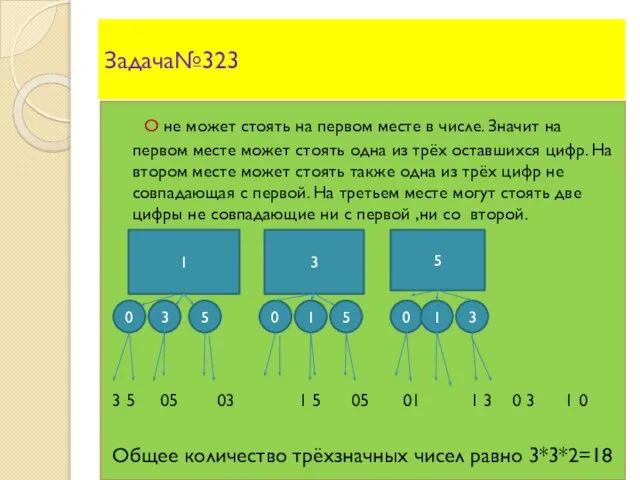
Задача№323
О не может стоять на первом месте в числе. Значит на первом месте может стоять одна из трёх оставшихся цифр. На втором месте может стоять также одна из трёх цифр не совпадающая с первой. На третьем месте могут стоять две цифры не совпадающие ни с первой ,ни со второй.
о второй циф
3 5 05 03 1 5 05 01 1 3 0 3 1 0
Общее количество трёхзначных чисел равно 3*3*2=18
1
3
5
0
3
5
0
1
5
0
1
3

Задача№356
На первом месте может стоять любая из пяти цифр, на втором месте может стоять любая из четырёх цифр , отличная от первой
3 5 7 9 1 5 7 9 1 3 7 9 1 3 5 9 1 3 5 7
1
3
5
7
9
Количество двузначных чисел равно 5*4=20

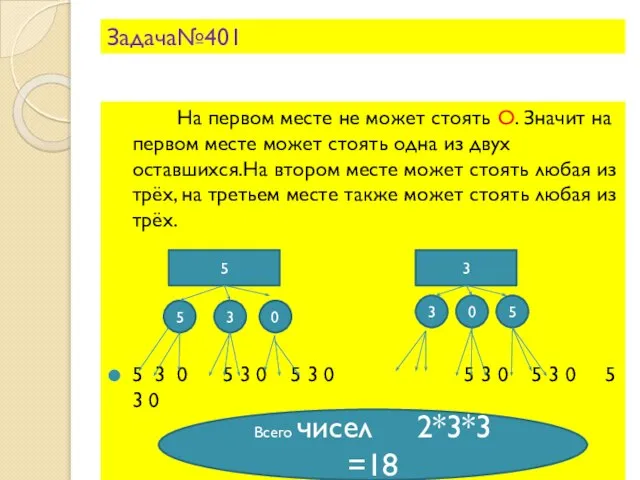
Задача№401
На первом месте не может стоять О. Значит на первом месте может стоять одна из двух оставшихся.На втором месте может стоять любая из трёх, на третьем месте также может стоять любая из трёх.
5 3 0 5 3 0 5 3 0 5 3 0 5 3 0 5 3 0
5
3
5
3
0
3
0
5
Всего чисел 2*3*3 =18

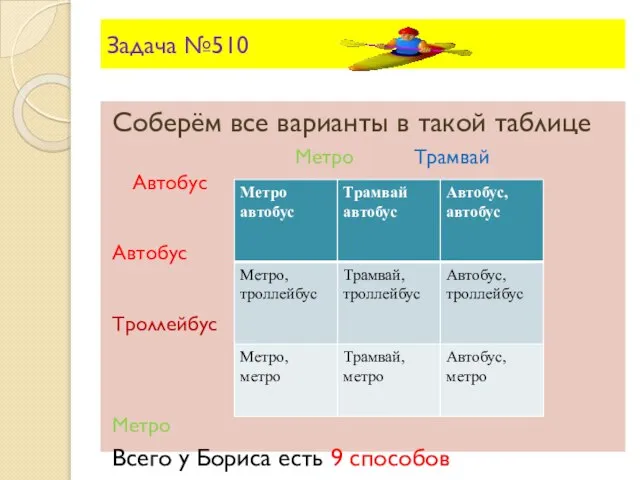
Задача №510
Соберём все варианты в такой таблице
Метро Трамвай Автобус
Автобус
Троллейбус
Метро
Всего у Бориса есть 9 способов

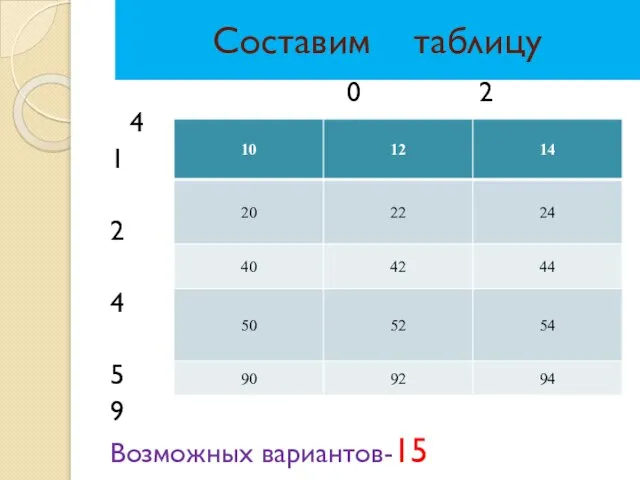
Рассмотрим ещё 2 задачи
Задача №1 Сколько чётных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
Составим таблицу: слева от первого поместим первые цифры искомых чисел, а выше первой строки- вторые цифры этих чисел. Т.к. в двузначном числе на первом месте может стоять любая цифра, кроме О, то строки будут отмечены цифрами1,2,4,5,9. Значит, в нашей таблице будет пять строк. На втором месте в искомом числе должна стоять чётная цифра, значит, столбцы будут отмечены цифрами 0,2,4.

Составим таблицу
0 2 4
1
2
4
5
9
Возможных вариантов-15

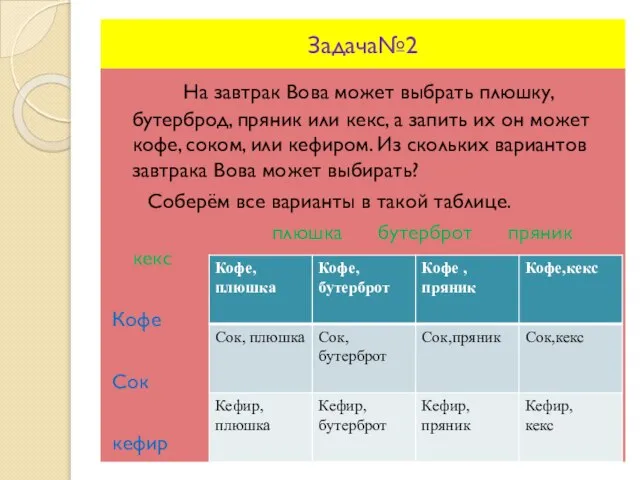
Задача№2
На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком, или кефиром. Из скольких вариантов завтрака Вова может выбирать?
Соберём все варианты в такой таблице.
плюшка бутерброт пряник кекс
Кофе
Сок
кефир

Ещё раз подтвердим правило умножения
Выбор еды и напитка происходит независимо, то в каждой клетке будет стоять один из возможных вариантов завтрака и, наоборот, любой вариант завтрака будет записан в одной клетке.
Значит 4*3=12.
Приятного аппетита!

Дерево возможных вариантов
Правило умножения для трёх, четырёх и т. д. испытаний можно объяснить ,с помощью геометрической модели, которую называют деревом возможных вариантов. Вы уже им пользовались в предыдущих задачах. Н.п в задачах №228, № 323. Дерево наглядно и позволяет всё учесть

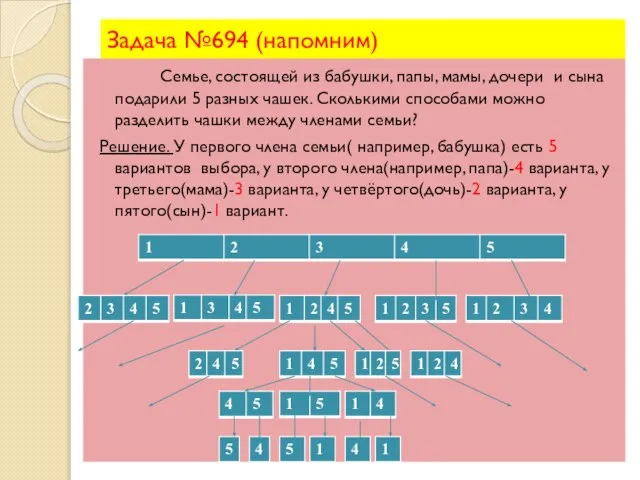
Задача №694 (напомним)
Семье, состоящей из бабушки, папы, мамы, дочери и сына подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами семьи?
Решение. У первого члена семьи( например, бабушка) есть 5 вариантов выбора, у второго члена(например, папа)-4 варианта, у третьего(мама)-3 варианта, у четвёртого(дочь)-2 варианта, у пятого(сын)-1 вариант.

Роскошное дерево вариантов! Правило умножения. Понятие факториала!
Получили, что каждому выбору чашки бабушки соответствует 4 возможных выбора папы, т.е. всего5*4 способов. После того как папа выбрал чашку, у мамы есть 3 варианта выбора, у дочери-2, у сына-1, т.е. всего 3*2*1способов. Окончательно получаем, что для решения задачи надо найти произведение 5*4*3*2*1 или 1*2*3*4*5=5!(пять-факториал)
Значит количество вариантов равно
5!=120
n!

Задача №807
Лена, Света, Маша, Катя и Наташа пришли к зубному врачу. Сколькими способами они могут встать в очередь?
Рассуждаем. Предположим Лена встаёт в очередь там где ей захочется, у неё есть 5 вариантов, тогда у Светы остаётся встать в очередь 4 вариантами, у Маши-3 вариантами,у Кати-2 вариантами и у Наташи-1 вариантом. По правилу умножения получаем 5*4*3*2*1=5!=120 способов.
Заглядывая в учебник 9 класса, мы выяснили, что в данной ситуации у нас получилось число перестановок из 5 элементов!

Понятие перестановки
Перестановкой из n элементов называется каждое расположение этих элементов в определённом порядке.
Когда Лена, Света, Катя, Маша, Наташа становились в очередь , они располагались в определённом порядке. Былоих5. Значит это перестановка из 5 злементов.
Подсмотрим формулу. Вот она Pn =n!
В нашем случае так и получилось P5=5!=120

Задача №835
Сколькими способами из 7 бусинок разных цветов можно составить ожерелье( с застёжкой)?
Рассуждаем. Т.к. застёжка в ожерелье не меняет своё место, то число перестановок из 7 элементов, т.е. 7!
1*2*3*4*5*6*7= 720*7=5040 способов

Задача №922
На книжную полку ставят 6 разных книг. Сколькими способами эти книги можно разместить на полке?
Рассуждаем. Положение 1-й книги будет определяться6 вариантами, положение второй книги-5 вариантами,3книги -4 вариантами, 4-й-соответственно-3вариантами,5-й-2 вариантами,6-й-1вариантом. Значит всего способов по правилу умножения6*5*4*3*2*1=6!=720
А можно по другому?. Да. Найдём число перестановок из 6 элементов т.е.P6 =6! =720

Задача № 1035
Кодовый замок имеет 6 кнопок. Чтобы его открыть, нужно нажать кнопки в определённой последовательности( набрать код). Сколько существует вариантов кода для этого замка
Рассуждаем. Явно нам необходимо найти количество перестановок из 6 элементов.т.е P6 =6! =720

Задача №1071
К полднику в детском саду на четырёхместный стол поставили сок, молоко, какао и компот. Сколькими способами четверо детей могут выбрать себе один из напитков?
Рассуждаем.Первый ребёнок имеет возможность выбрать любой стакан 4вариантами, второму остаётся выбор из 3 вариантов, третьему придётся выбирать из 2 вариантов, четвёртому остаётся выбор одного варианта. По правилу умножения -количество вариантов равно 4*3*2*1=4!=24
А можно по –другому? Да. Количество перестановок
P4 =4! =24

Задача№1728
Сколькими способами 4 пассажира могут разместиться в четырёхместном купе?
Рассуждаем. Первый пассажир может выбрать любое место из 4, второму остаётся выбирать из 3 вариантов, третьему из 2вариантов, ну а 4 пассажир займёт то место, которое останется. Значит количество способов 4*3*2*1=24, а по -другому P4 =4!=24
Счастливого пути!