Консервативное звено 2 порядка

Звено второго порядка (колебательное)
Такие звенья описываются дифференциальным уравнением вида:
где,
y – выходной сигнал
U – входной сигнал
a,b – коэффициенты уравнения
t - время
Для звена второго порядка характерны параметры:
Где,
T — постоянная времени (в секундах);
ξ — коэффициент затухания (безразмерная величина);
k — передаточный коэффициент.
Различают три вида звеньев второго порядка

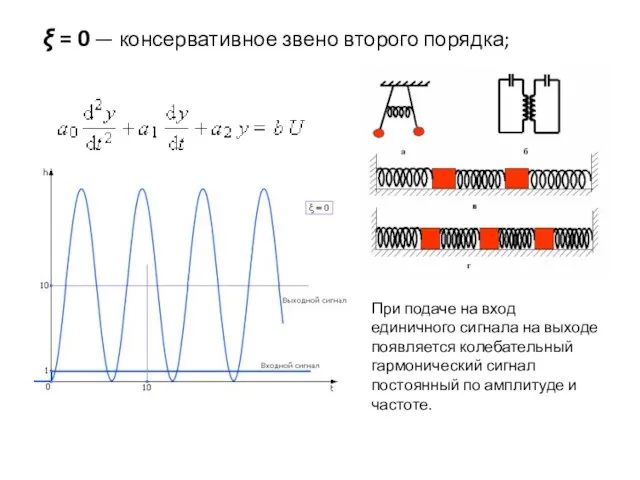
ξ = 0 — консервативное звено второго порядка;
При подаче на вход единичного сигнала на выходе появляется колебательный гармонический сигнал постоянный по амплитуде и частоте.

0 < ξ < 1 — колебательное звено второго порядка;
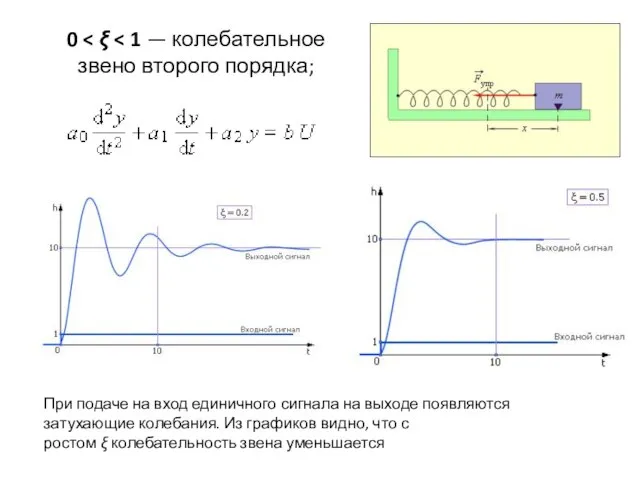
При подаче на вход единичного сигнала на выходе появляются затухающие колебания. Из графиков видно, что с ростом ξ колебательность звена уменьшается

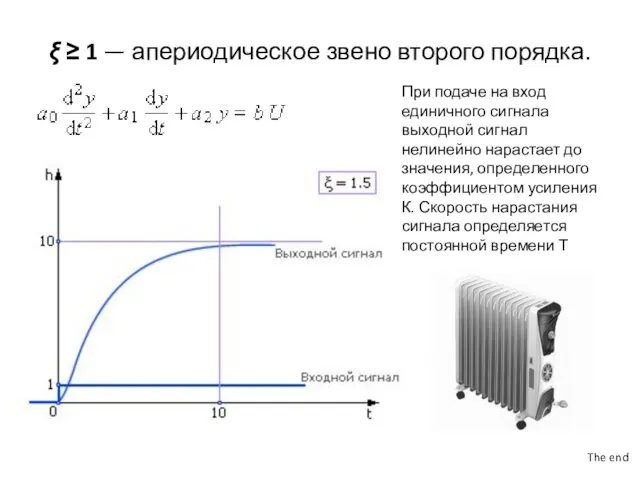
ξ ≥ 1 — апериодическое звено второго порядка.
При подаче на вход единичного сигнала выходной сигнал нелинейно нарастает до значения, определенного коэффициентом усиления К. Скорость нарастания сигнала определяется постоянной времени Т
The end

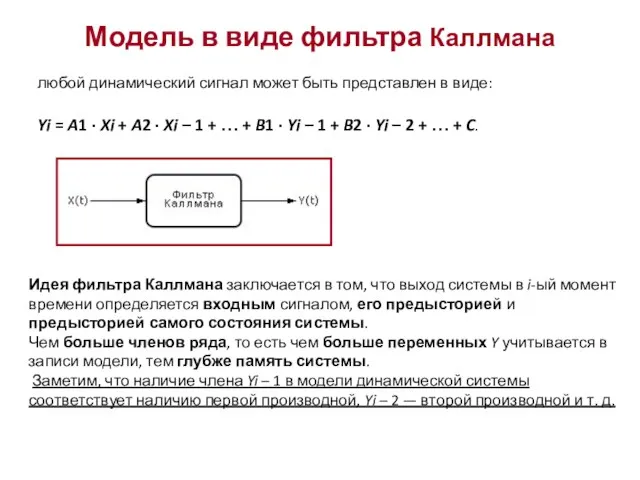
Модель в виде фильтра Каллмана
любой динамический сигнал может быть представлен в виде:
Yi = A1 · Xi + A2 · Xi – 1 + … + B1 · Yi – 1 + B2 · Yi – 2 + … + C.
Идея фильтра Каллмана заключается в том, что выход системы в i-ый момент времени определяется входным сигналом, его предысторией и предысторией самого состояния системы.
Чем больше членов ряда, то есть чем больше переменных Y учитывается в записи модели, тем глубже память системы.
Заметим, что наличие члена Yi – 1 в модели динамической системы соответствует наличию первой производной, Yi – 2 — второй производной и т. д.

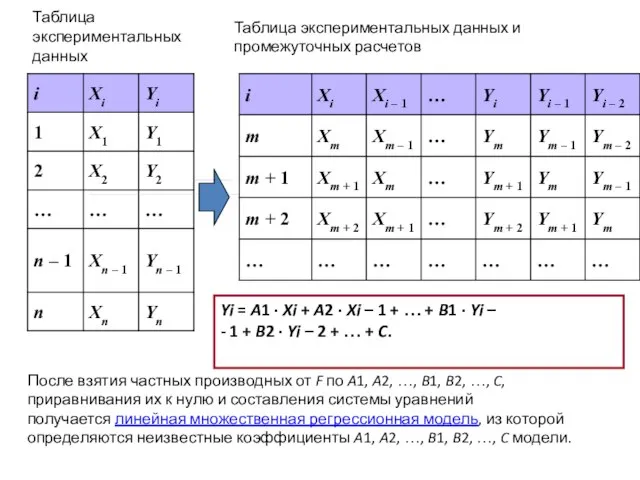
Таблица
экспериментальных
данных
Таблица экспериментальных данных и промежуточных расчетов
После взятия частных производных от F по A1, A2, …, B1, B2, …, C, приравнивания их к нулю и составления системы уравнений получается линейная множественная регрессионная модель, из которой определяются неизвестные коэффициенты A1, A2, …, B1, B2, …, C модели.
Yi = A1 · Xi + A2 · Xi – 1 + … + B1 · Yi – - 1 + B2 · Yi – 2 + … + C.

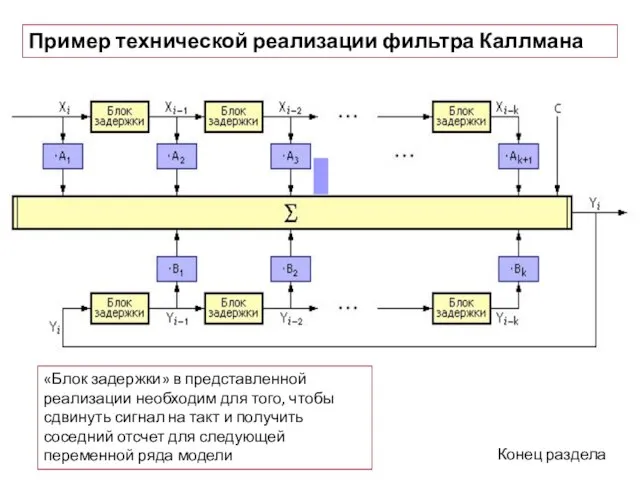
Пример технической реализации фильтра Каллмана
«Блок задержки» в представленной реализации необходим для того, чтобы сдвинуть сигнал на такт и получить соседний отсчет для следующей переменной ряда модели
Конец раздела

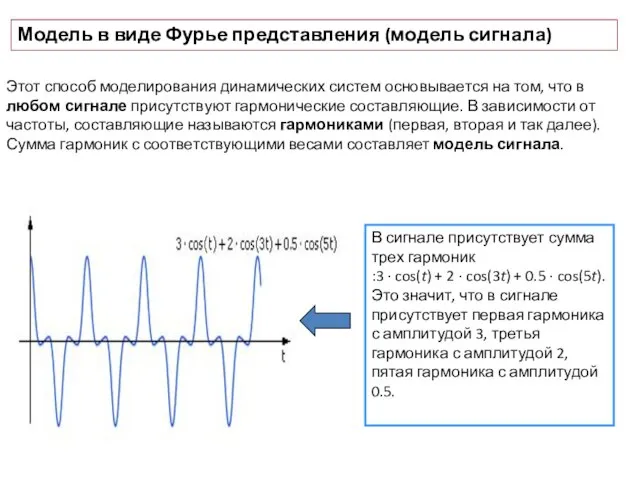
Модель в виде Фурье представления (модель сигнала)
Этот способ моделирования динамических систем основывается на том, что в любом сигнале присутствуют гармонические составляющие. В зависимости от частоты, составляющие называются гармониками (первая, вторая и так далее). Сумма гармоник с соответствующими весами составляет модель сигнала.
В сигнале присутствует сумма трех гармоник :3 · cos(t) + 2 · cos(3t) + 0.5 · cos(5t).
Это значит, что в сигнале присутствует первая гармоника с амплитудой 3, третья гармоника с амплитудой 2, пятая гармоника с амплитудой 0.5.

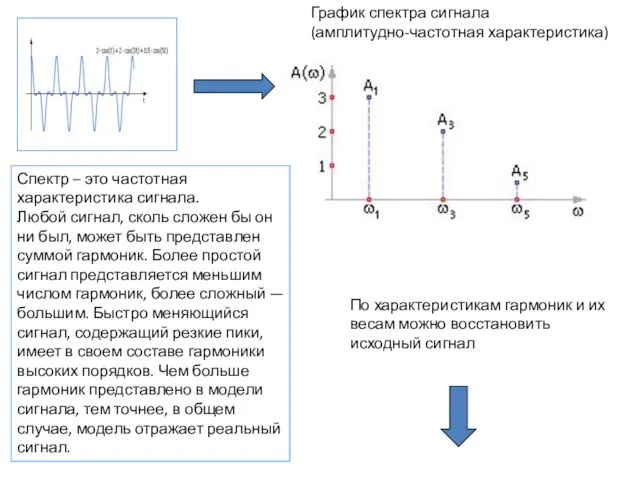
График спектра сигнала
(амплитудно-частотная характеристика)
Спектр – это частотная характеристика сигнала.
Любой сигнал, сколь сложен бы он ни был, может быть представлен суммой гармоник. Более простой сигнал представляется меньшим числом гармоник, более сложный — большим. Быстро меняющийся сигнал, содержащий резкие пики, имеет в своем составе гармоники высоких порядков. Чем больше гармоник представлено в модели сигнала, тем точнее, в общем случае, модель отражает реальный сигнал.
По характеристикам гармоник и их весам можно восстановить исходный сигнал

……….
……….
……….
……….
Прямое преобразование Фурье
где, A,B – веса соответствующих гармоник,
i – номер гармоники,
p – период.