Корреляционные зависимости

Определение
Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями.
Раздел математической статистики, который исследует такие зависимости, называется корреляционным анализом.
Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости.

Пусть важной характеристикой некоторой сложной системы является фактор А. На него могут оказывать влияние одновременно многие другие факторы: В, С, D и так далее.
Обычно требуется требуется определить:
оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А;
какие из факторов В, С, D и так далее оказывают наибольшее влияние на фактор А.

Пример для первого типа задач
Фактором А является средняя успеваемость учащихся школы, фактором В — финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п.
Здесь влияние фактора В на фактор А не очевидно.

Сбор статистики

Коэффициент корреляции
Мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции.
Коэффициент корреляции (обычно обозначаемый греческой буквой р) есть число, заключенное в диапазоне от -1 до +1;
Если это число по модулю близко к |1|, то имеет место сильная корреляция, если к 0, то слабая;
Близость р к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное;

В Excel функция вычисления коэффициента корреляции называется КОРРЕЛ и входит в группу статистических функций.
Она запрашивает два диапазона значений и возвращает коэффициэнт корелляции.
Для нашего примера р = 0,500273843. Эта величина гово­рит о среднем уровне корреляции.

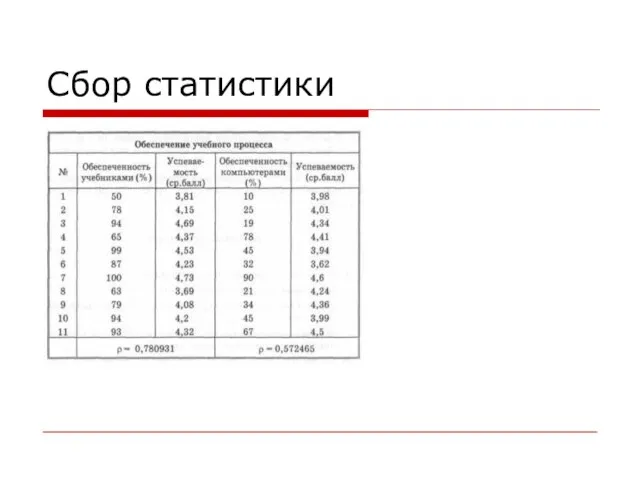
Пример для второго типа задач
Провести исследование по определению зависимости успеваемости учащихся старших классов от двух факторов: обеспеченности школьной библиотеки учебниками и обеспеченности школы компьютерами.

Сбор статистики

Корреляция между обеспеченностью учебниками и успеваемостью сильнее, чем корреляция между компьютерным обеспечением и успеваемостью.
Отсюда можно сделать вывод, что пока еще книга остается более значительным источником знаний, чем компьютер.