Содержание
- 2. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 Литература Моделирование рисковых ситуаций в экономике и
- 3. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Функция полезности в условиях риска Пусть
- 4. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Наименьший возможный убыток – вариант A
- 5. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Существует ли общее правило выбора? Ответ
- 6. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Для рискового выбора существует безрисковый эквивалент:
- 7. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Существует правило задания выбора, равноценного любому
- 8. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Аксиомам Неймана-Моргенштерна отвечает правило принятия решения
- 9. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Функция u (.) выпукла, если из
- 10. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1.
- 11. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1.
- 12. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.1. Пусть f ($) = –(1/k)$+1, т.е.
- 13. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.2. Оптимальное планирование в условиях риска Найти
- 14. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.2. Решение: max(0.05f ($1)+.95f ($2) | $1=-2x1+2x2;
- 15. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.3. Подготовка исходных данных о риске Вероятность
- 16. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.3. Подготовка исходных данных о риске Вероятность
- 17. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.3. Подготовка исходных данных о риске Вероятность
- 18. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.4. Моделирование многоэтапного процесса принятия решений Туроператор
- 19. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.4. Решаем задачу. Переменные: Априорное решение (когда
- 20. Математические методы планирования риска (с) Н.М. Светлов, 2007 /21 1.4. Решаем задачу (cont.) Целевая функция: максимум
- 22. Скачать презентацию



















 Степени сравнения
Степени сравнения «Опыт внедрения автоматизированного учета социальных услуг в МУ «ЦСО» г.Таганрога»
«Опыт внедрения автоматизированного учета социальных услуг в МУ «ЦСО» г.Таганрога» Применение оптических волоконных световодов для сверхплотной и сверхбыстройпередачи информации
Применение оптических волоконных световодов для сверхплотной и сверхбыстройпередачи информации Творческое объединение волейбол. Презентация достижений
Творческое объединение волейбол. Презентация достижений Церковь Великого Устюга Спасо-Преображенская
Церковь Великого Устюга Спасо-Преображенская СТРОИТЕЛЬНЫЙ КЛАСТЕР ХАБАРОВСКОГО КРАЯ
СТРОИТЕЛЬНЫЙ КЛАСТЕР ХАБАРОВСКОГО КРАЯ ПРЕЗЕНТАЦИЯ ВЫПОЛНЕННЫХ РАБОТ (ОКАЗАННЫХ УСЛУГ)
ПРЕЗЕНТАЦИЯ ВЫПОЛНЕННЫХ РАБОТ (ОКАЗАННЫХ УСЛУГ)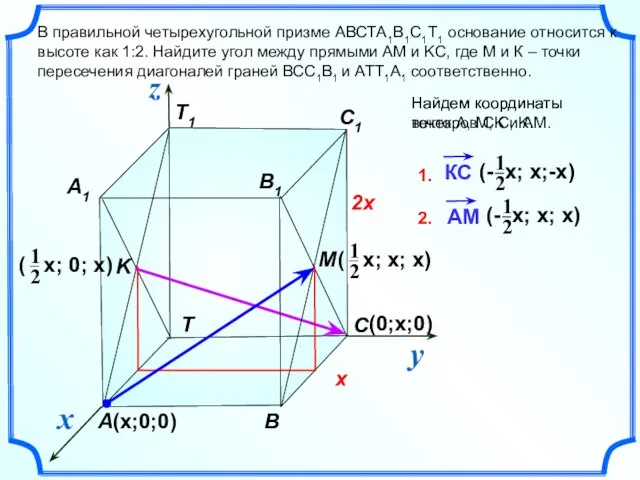 (0;x;0)
(0;x;0) L_2_1_Stali_klassifikatsia_stalei_774
L_2_1_Stali_klassifikatsia_stalei_774 Презентация на тему дни воинской славы россии
Презентация на тему дни воинской славы россии  простые механизмы в нашей жизни
простые механизмы в нашей жизни Fly (пилотам)
Fly (пилотам) А.М.Горчаков
А.М.Горчаков Коллекция дидактических игр для устного счёта 1 класс
Коллекция дидактических игр для устного счёта 1 класс Упражнения для мозга
Упражнения для мозга Проектирование кондитерских зданий
Проектирование кондитерских зданий Хэллоуин история праздника
Хэллоуин история праздника Perfect print
Perfect print «Влияние электромагнитных волн на живые организмы»
«Влияние электромагнитных волн на живые организмы» жизнь и творчество шолохова
жизнь и творчество шолохова Here’s Why Apple May Win the Automotive Infotainment Space
Here’s Why Apple May Win the Automotive Infotainment Space Самоконтроль в процессе занятий физкультурой и спортом (занятие 5)
Самоконтроль в процессе занятий физкультурой и спортом (занятие 5) Модуль 1
Модуль 1 Радченко А.В., Костюк С.В.
Радченко А.В., Костюк С.В. Презентация на тему Русская философия XIX века
Презентация на тему Русская философия XIX века Цвет в рекламном сообщении
Цвет в рекламном сообщении Исследовательская работа по теме: «Выращивание кристаллов в домашних условиях» ученика 3 класса
Исследовательская работа по теме: «Выращивание кристаллов в домашних условиях» ученика 3 класса  Компьютерная техника
Компьютерная техника