Слайд 2План лекции
Свободные незатухающие гармонические колебания:
Пружинный маятник
Математический маятник
Физический маятник
Затухающие колебания с вязким

трением.
Вынужденные колебания. Резонанс.
Параметрический резонанс.
Слайд 3Колебательные процессы
Колебание – изменение состояния системы по периодическому или почти периодическому закону:

маятник часов, груз на пружине, гитарная струна, давление воздуха в звуковой волне.
Свободные (или собственные) колебания: колебания в системе, предоставленной самой себе:
шарик в лунке, маятник.
Вынужденные колебания – колебания под действием внешней периодической силы: вибрации моста, качели.
Автоколебания, параметрические колебания.
Слайд 4Свободные незатухающие гармонические колебания.
Пружинный маятник
mx” = - kx ⇨ mx” + kx

= 0 ⇨
x” + ω02x = 0 – дифференциальное уравнение гармонических колебаний (ω02 = k/m)
x = Acos(ω0t + φ0) – гармоническое колебание
A – амплитуда колебаний
ω0 – циклическая частота
φ0 – начальная фаза
ω0t + φ0 – фаза колебаний
T = 2π/ ω0 – период колебаний
Изохронность: ω0 – определяется только свойствами системы и не зависит от амплитуды.
F = -kx – квазиупругая возвращающая сила
Слайд 5Скорость и ускорение при гармонических колебаниях
Смещение:
x = Acos(ω0t + φ0)
Скорость:
v =

x’ = - ω0Asin(ω0t + φ0) = ω0Acos(ω0t + φ0 + π/2);
v0 = ω0A – амплитуда скорости;
скорость опережает смещение x по фазе на π/2.
Ускорение
a = - ω02Acos(ω0t + φ0) = ω02Acos(ω0t + φ0 + π)
a0 = ω02A – амплитуда ускорения;
ускорение в противофазе со смещением
Слайд 6Энергия гармонических колебаний
Потенциальная энергия:
П = kx2/2 = ½kA2cos2(ω0t + φ0)
Кинетическая энергия:
K

= mv2/2 = ½mω02A2sin2(ω0t + φ0) =
½кA2sin2(ω0t + φ0)
Полная энергия:
Е = П + K = const = ½kA2 = ½mv02
Для гармонических колебаний:
= <П> = ½E
Слайд 7Энергетический метод для колебательных систем с одной степенью свободы
q – обобщённая координата

(смещение, угол поворота)
q’ – обобщённая скорость (скорость смещения, угловая скорость)
Уравнение энергии: ½ κq2 +½ μq’2 = const
П = ½ κq2 – потенциальная энергия
K = ½ μq’2 – кинетическая энергия
ω2 = κ/μ – циклическая частота
κ – эффективная жёсткость системы
μ – инерционность системы
Слайд 8Математический маятник.
Математический маятник – материальная точка на нерастяжимой лёгкой нити в

поле тяжести Земли.
Энергетический метод:
θ – угол отклонения нити от вертикали (обобщённая координата).
Потенциальная энергия:
П = mgL(1 – cosθ) ≈ ½ mgLθ2 = ½ кθ2
k = mgL – эффективная жёсткость
Кинетическая энергия:
K = ½ m(Lθ’)2 = ½ mL2 θ’2 = ½ μθ’2 μ = ½ mL2 – инерционность системы
Уравнение колебаний: ½кθ2 + ½ μθ’2 = const
ω02 = к/μ = g/L; T = 2π/ω0 = 2π(L/g)1/2
Слайд 9Ангармонический математический маятник
½кθ2 + ½ μθ’2 = const ⇨ θ” + ω02

θ = 0 – линеаризованное уравнение
θ” + ω02sinθ = 0 – нелинеаризованное ангармоническое уравнение;
T = T0(1 + θ02/16 + 9θ04/64 + …) – период зависит от амплитуды (θ0 – амплитуда)
Слайд 10Физический маятник
Физический маятник - твёрдое тело, совершающее колебания вокруг неподвижной горизонтальной оси.
Энергетический

метод:
Потенциальная энергия:
П = mga(1 – cosθ) ≈ ½ mgaθ2
Кинетическая энергия:
K = ½Iθ’2, I = Ic + ma2 - момент инерции относительно оси O
Уравнение колебаний: ½mgaθ2 + ½ Iθ’2 = const
ω02 = mga/I; T = 2π/ω0 = 2π(l/mga)1/2
Слайд 11Приведённая длина. Центр качания. Теорема Гюйгенса.
Оборотный маятник и измерение g
Lпр =

I/ma – длина математического маятника с тем же периодом колебаний
Lпр = I/ma = (Ic + ma2)/ma = a + Ic/ma
Центр качания О’ расположен на прямой ОС расстоянии Lпр от точки подвеса O
Теорема Гюйгенса
Точка подвеса и центр качания являются “сопряжёнными” точками: если маятник подвесить за центр качания, то его период не изменится.
Доказательство: Lпр = a + Ic/ma ⇨ a2 - Lпрa + Ic/m = 0 ⇨
a1 + a2 = Lпр
Оборотный маятник и измерение g: экспериментально определяют расстояние между сопряжёнными точками ОО’ = Lпр и рассчитывают g по формуле: g = Lпрω02
Слайд 12Крутильные колебания
Диск на упругой нити:
Момент упругих сил Mz = - kθ, k

– коэффициент “крутильной” жёсткости
I0θ” = - kθ ⇨ θ” + (k/I0)θ = 0 ⇨ ω02 = k/I0
Слайд 13Затухающие колебания.
Сила вязкого трения Fтр = -βv
mx” = - kx –

βv ⇨ mx” + βv + kx = 0 ⇨
x” + 2γx’ + ω02 x = 0 - дифференциальное уравнение колебаний с затуханием;
γ = β/2m – коэффициент затухания
ω02 = k/m – собственная частота
если γ < ω0,то
x = а0e-γtcos(ωt + φ0),
ω = (ω02 – γ2)1/2 – частота затухающих колебаний; а0e-γt – амплитуда затухающих колебаний
Слайд 14Характеристики затухающих колебаний
Время релаксации τ – это время, за которое амплитуда

колебаний уменьшается в e раз:
τ = 1/ γ
Логарифмический декремент затухания:
λ = ln[a(t)/a(t + T)] = γT = T/τ
Число колебаний, за которое амплитуда уменьшается в e раз
Ne = τ/T = 1/λ
Слабое затухание Ne = τ/T = ω/2πγ >> 1 ⇨
γ << ω ≈ ω0
Слайд 15Диссипация энергии. Добротность.
dE/dt = -βv2 - мощность силы трения
dE/dt = -βv2 =

-(2β/m) (mv2/2) = - 4γK
Слабое затухание: γ << ω0 ⇨ = ½ E ⇨
dE/dt = - 2γE ⇨ E = E0e-2γt
Убыль энергии за период ΔЕT = 2γTE
Убыль энергии при изменении фазы на 1 рад:
ΔЕ = ΔЕT/2π = (2γ/ω)E0
Добротность:
Q = E/ΔЕ = ω/2γ = πNe
Слайд 16Вынужденные колебания. Векторные диаграммы. Резонанс.
mx” + βv + kx = Fcosωt ⇨
x”

+ 2γx’ + ω02x = fcos ωt, f = F/m
Вынужденные колебания ищем в виде:
x = Bcos(ωt – φ)
Векторная диаграмма:
x = Acos (ωt + φ0) проекция на ось OX радиус-вектора длиной A, вращающегося против часовой стрелки с угловой скоростью ω от начального положения φ0
Слайд 17Вынужденные колебания. Векторные диаграммы. Резонанс.
Из векторной диаграммы:
амплитуда
B = f/((ω2 – ω02)) +

4γ2ω2)1/2
Фаза
tg φ = 2γω/(ω02– ω2)
В резонансе (при малых γ)
Bmax ≈ B(ω0) = f/2γω0 ⇨ Bmax/Bстат = ω0/2γ = Q
Вблизи резонанса:
B = Bmaxγ/((ω – ω0)2 + γ2)1/2 ⇨ ширина резонансной кривой Δω = 2γ
















 Решение уравнений
Решение уравнений Грузовое устройство
Грузовое устройство Катаргина Наталья Юрьевна.
Катаргина Наталья Юрьевна. Новогоднее представление Мышеловка для Деда Мороза
Новогоднее представление Мышеловка для Деда Мороза Экосистема Digital-маркетинга в России: Основы навигациии X Саммит Брендов-Лидеров 7 июня 2011. - презентация
Экосистема Digital-маркетинга в России: Основы навигациии X Саммит Брендов-Лидеров 7 июня 2011. - презентация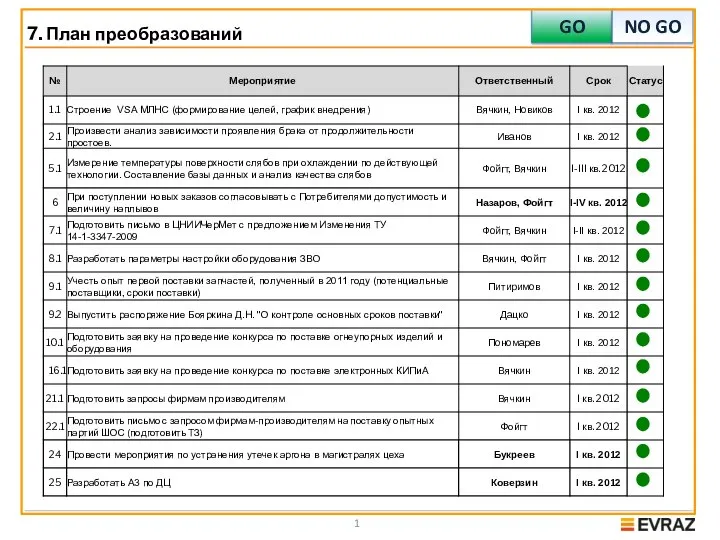 План преобразований. Отслеживание результатов
План преобразований. Отслеживание результатов Порядок получения статуса субъекта оптового рынка и права на участие в торговой системе оптового рынка
Порядок получения статуса субъекта оптового рынка и права на участие в торговой системе оптового рынка  Поводы и основания к возбуждению уголовного дела
Поводы и основания к возбуждению уголовного дела Вольфганг Амадей Моцарт
Вольфганг Амадей Моцарт Съемки подземных сооружений и коммуникаций
Съемки подземных сооружений и коммуникаций Проблема истинной человечности в рассказе К. Паустовского “Телеграмма”
Проблема истинной человечности в рассказе К. Паустовского “Телеграмма” Вакцинация детей с перинатальным контактом по ВИЧ и ВИЧ-инфицированных
Вакцинация детей с перинатальным контактом по ВИЧ и ВИЧ-инфицированных Оценка рисков при проведении форвардных сделок
Оценка рисков при проведении форвардных сделок Управления их классификация
Управления их классификация Стратегия бизнес - проекта «Магазин без очередей и касс»
Стратегия бизнес - проекта «Магазин без очередей и касс» Город и транспорт
Город и транспорт Проектная грамотность. Как правильно подготовить заявку на финансирование проекта и реализовать задуманное
Проектная грамотность. Как правильно подготовить заявку на финансирование проекта и реализовать задуманное Презентация на тему Ирак
Презентация на тему Ирак Объекты газоснабжения и водоснабжения, планируемые к реализации в 2020 году
Объекты газоснабжения и водоснабжения, планируемые к реализации в 2020 году Ремонт электролизёров на месте установки
Ремонт электролизёров на месте установки Презентация на тему Японское море
Презентация на тему Японское море Ранний железный век в Казахстане
Ранний железный век в Казахстане Passato Reg
Passato Reg Легендарное восклицание «Эврика!», принадлежит Архимеду , «Я нашел!» Легендарное восклицание «Эврика!», принадлежит Архимеду , «
Легендарное восклицание «Эврика!», принадлежит Архимеду , «Я нашел!» Легендарное восклицание «Эврика!», принадлежит Архимеду , « Этические и правовые нормы информационной деятельности человека
Этические и правовые нормы информационной деятельности человека Лекция 5 Модель классов предметной области (1)
Лекция 5 Модель классов предметной области (1) Осторожно - мошенники
Осторожно - мошенники Модернизация государственной семейной политики в современной России: (экстра)ординарный поворот к пронатализму
Модернизация государственной семейной политики в современной России: (экстра)ординарный поворот к пронатализму