Линейная функция и линейные уравнения вокруг нас

1. Линейное уравнение
с одной переменной
2. Алгоритм решения линейного уравнения. Примеры уравнений
3. Примеры решения задач с помощью линейных уравнений
4. Линейная функция
5. Частные случаи линейной функции
6. Прямая пропорциональность
7. Линейная функция и линейные уравнения вокруг нас
8. Используемая литература
Содержание:

Линейное уравнение с одной переменной.
Линейное уравнение с одной переменной — это уравнение вида ax = b, где х – переменная, a и b – некоторые числа.
Например: 3х+15=0;
6,4х=0,4;
- х = - 3,7.

Линейное уравнение с одной переменной
имеет единственный корень,
если a≠0;
2) имеет бесконечное множество корней, если a=0; b=0;
3) не имеет корней, если a=0; b≠0.

1 случай: ax = b, a≠0
Примеры:

Например:
2 случай: ax = b, a=0, b=0

3 случай: ax = b, a=0, b ≠ 0
Например:

Алгоритм решения уравнений, сводящихся к линейным.
1. Раскрыть скобки в уравнении, если они есть.
2. Перенести слагаемые с переменной в одну часть уравнения, а слагаемые без переменной – в другую часть уравнения, изменив при этом их знаки.
3. Привести подобные слагаемые.
4. Найти корень уравнения.
5. Выполнить проверку.
6. Записать ответ.

Примеры уравнений,
сводящихся к линейным.

Примеры уравнений,
сводящихся к линейным.

Примеры уравнений,
сводящихся к линейным.

Примеры уравнений,
сводящихся к линейным.

Решение задач с помощью линейных уравнений.

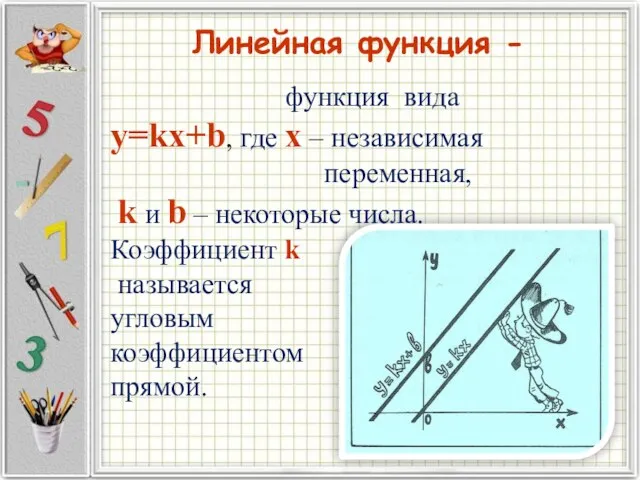
Линейная функция -
функция вида
y=kx+b, где x – независимая
переменная,
k и b – некоторые числа.
Коэффициент k
называется
угловым
коэффициентом
прямой.

Свойства линейной функции
1. Область определения – любое число.
2. Область значений – любое число.
3. При прямая образует острый угол с осью абсцисс.
4. При прямая образует тупой угол с осью абсцисс.
5. При прямая параллельна оси абсцисс.
6. График линейной функции проходит через точку (0;в).
7. При прямая
проходит через начало
координат.

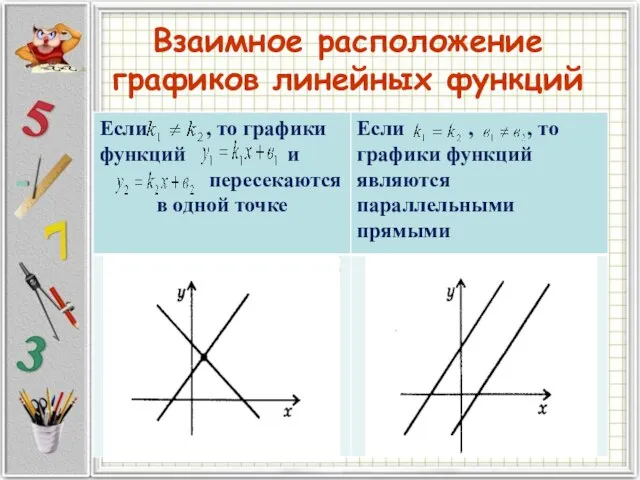
Взаимное расположение
графиков линейных функций

Частные случаи
линейной функции.

Прямая
пропорциональность -
функция вида
y=kx, где x – независимая
переменная,
k – число, k .
.
Например:
зависимость пути S от времени t при постоянной скорости v .

Свойства прямой пропорциональности
Область определения – любое число.
Область значений – любое число.
При прямая расположена в 1 и 3 координатной четверти, образует острый угол с осью абсцисс.
При прямая расположена во 2 и 4 координатной четверти, образует тупой угол с осью абсцисс.
График проходит через начало координат.
Переменные х и у
изменяются прямо
пропорционально
на всей числовой прямой.

Линейная функция в пословицах

Используемая литература.
Учебник «Алгебра – 7», под ред. С.А.Теляковского. Москва «Просвещение» 2011г.
Учебник "Алгебра - 7", ред. Мордкович А.Г.
Дидактический материал «Самостоятельные и контрольные работы. Алгебра, геометрия – 7». А. П. Ершова, В. В. Голобородько, А. С.Ершова. Москва «Илекса», 2011г.
Дидактический материал «Алгебра – 7», под ред. Л.И. Звавич и др.
«Задачи по алгебре 6 – 8 класс», ред. Д.К. Фадеев и др.
Интернет – ресурсы. http://ru.math.wikia.com/wiki/ ,
шаблон презентации Ранько Е. А.
http://pedsovet.su/