Логика и техника инвестиционных расчетов

Существенным является такое понятие как «временнАя ценность денег», задействованных в инвестиционном процессе.
Важность учета фактора времени обусловлена принципом неравноценности денег, относящихся к различным моментам времени: равные по абсолютной величине денежные суммы "сегодня" и "завтра" оцениваются по разному.
Какие деньги «стоят» дороже, сегодняшние или завтрашние?
С чем это связано?

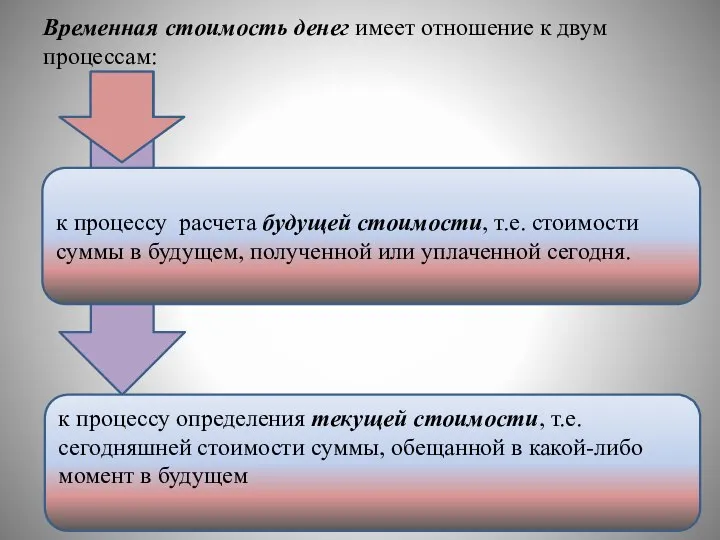
Временная стоимость денег имеет отношение к двум процессам:
к процессу расчета будущей стоимости, т.е. стоимости суммы в будущем, полученной или уплаченной сегодня.
к процессу определения текущей стоимости, т.е. сегодняшней стоимости суммы, обещанной в какой-либо момент в будущем

Простейшим примером инвестирования является однократное предоставление в долг некоторой суммы
PV (Present Value — текущая стоимость )
для того, что бы через некоторое время t получить некоторую большую сумму
FV (Future Value - будущая стоимость)

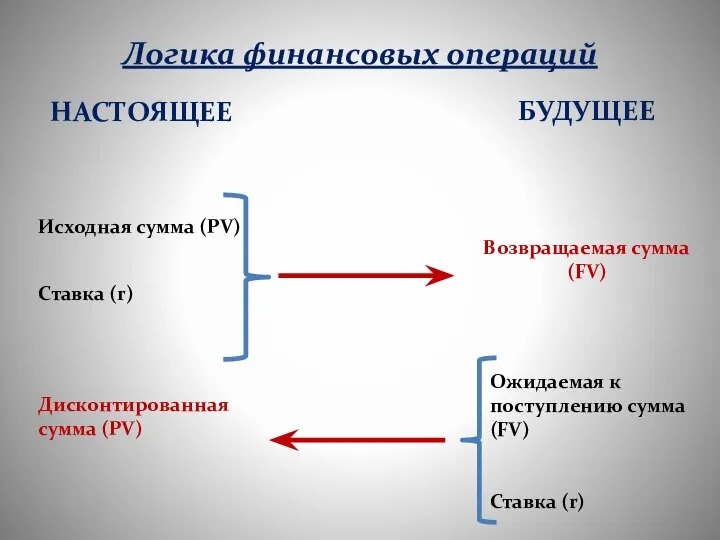
Логика финансовых операций
НАСТОЯЩЕЕ
Исходная сумма (PV)
Ставка (r)
Дисконтированная сумма (PV)
БУДУЩЕЕ
Возвращаемая сумма (FV)
Ожидаемая к поступлению сумма(FV)
Ставка (r)

О какой «загадочной» ставке r идет речь в предыдущем слайде?
Результативность сделки по передаче в долг некоторой величины PV с последующей отдачей некоторой большей суммы FV можно охарактеризовать двояко:
с помощью абсолютного показателя —
прироста (FV — PV),
путем расчета некоторого относительного показателя – коэффициента, называемого ставкой (r).

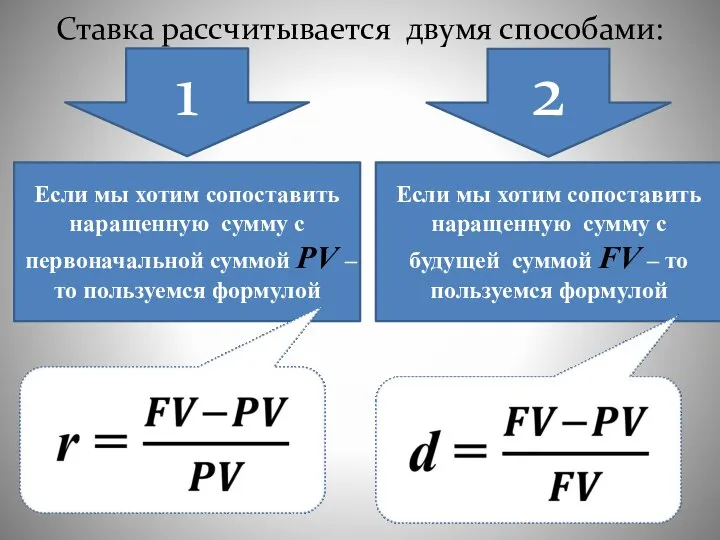
Ставка рассчитывается двумя способами:
1
2
Если мы хотим сопоставить наращенную сумму с первоначальной суммой PV – то пользуемся формулой
Если мы хотим сопоставить наращенную сумму с будущей суммой FV – то пользуемся формулой

Величина r носит название «процентная ставка», «процент», «ставка процента», «норма прибыли»
Величина d носит название «учетная ставка», «дисконтная ставка», «дисконт», «ставка дисконтирования»

В банк на депозитный счет внесли
1 000 руб., через год сумма возросла до 1200 руб.

Если в финансовых вычислениях заданы исходная сумма и ставка и следует найти некую величину в будущем, то
то такой процесс называется наращением,
будущая денежная сумма — наращенной суммой,
используемая в операции ставка — ставкой наращения.
В этом случае речь идет о движении денежного
потока от настоящего к будущему

Если в вычислениях заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, и следует найти денежную сумму на текущий момент то
такой процесс называют - дисконтированием
искомая величина называется дисконтированной суммой (иногда используется термин приведенная сумма),
используемая в операции ставка — ставкой дисконтирования.
В этом случае речь идет о движении денежного
потока от будущего к настоящему

Определение современной величины РV «отталкиваясь» от наращенной будущей суммы FV называется дисконтированием
Определение величины наращенной суммы FV «отталкиваясь» от первоначальной величины PV – называется
компаундингом

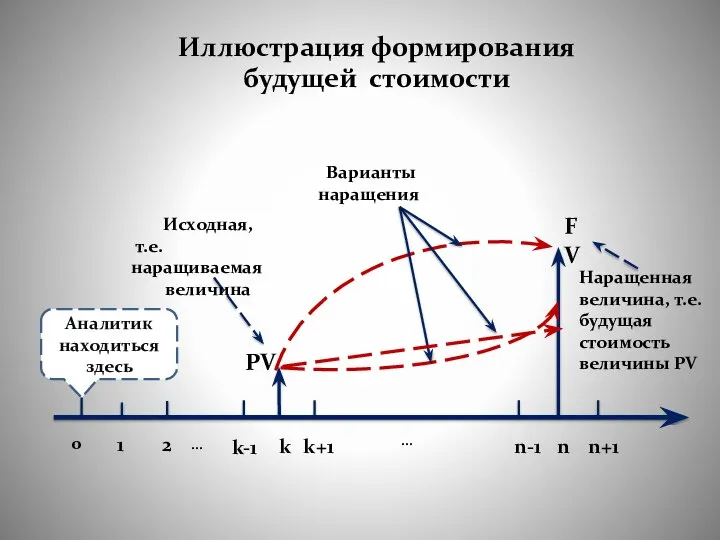
Иллюстрация формирования
будущей стоимости
Аналитик находиться здесь
0
1
2
…
k-1
k
k+1
…
n-1
n
n+1
FV
Наращенная
величина, т.е.
будущая стоимость
величины PV
Варианты
наращения
Исходная,
т.е. наращиваемая
величина
PV

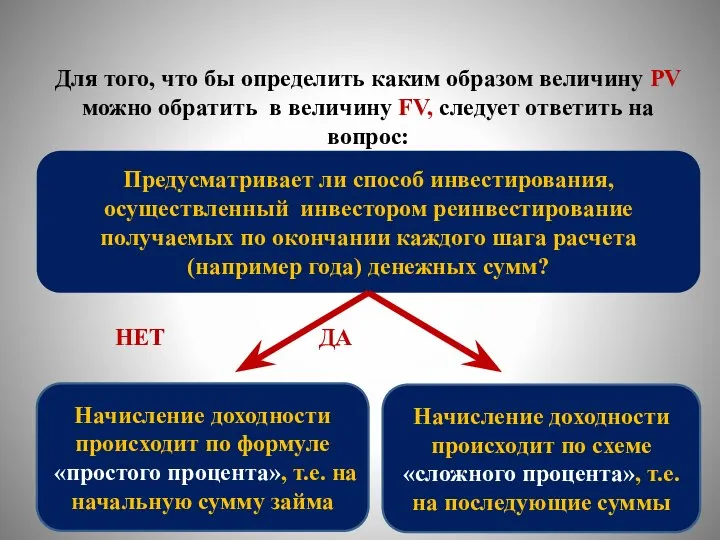
Для того, что бы определить каким образом величину PV можно обратить в величину FV, следует ответить на вопрос:
НЕТ ДА
Предусматривает ли способ инвестирования, осуществленный инвестором реинвестирование получаемых по окончании каждого шага расчета (например года) денежных сумм?
Начисление доходности происходит по формуле «простого процента», т.е. на начальную сумму займа
Начисление доходности происходит по схеме «сложного процента», т.е. на последующие суммы

Простые ставки ссудных процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает периодам начисления (и составляет, как правило, срок до одного года) или когда после каждого интервала начисления кредитору выплачиваются проценты
Схема простых процентов предполагает неизменность базы, с которой происходит начисление процентов

Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей ранее начисленные и не востребованные инвестором проценты.
В этом случае происходит капитализация процентов по мере их начисления, т. е. база, с которой начисляются проценты, все время возрастает.

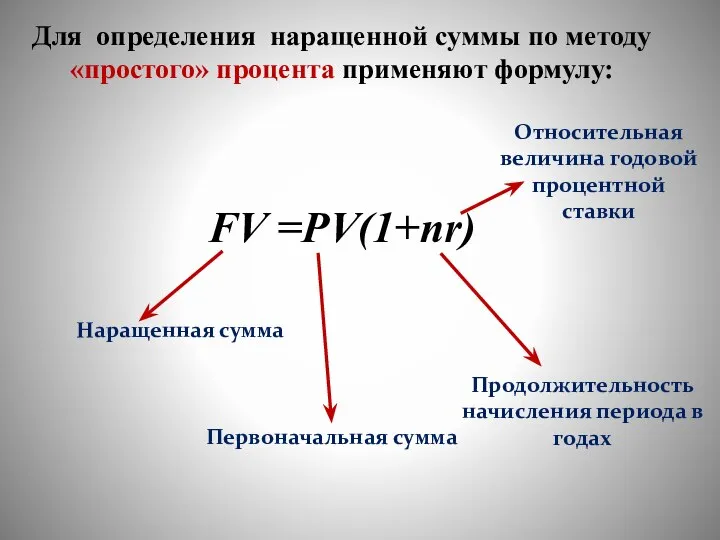
Для определения наращенной суммы по методу «простого» процента применяют формулу:
FV =PV(1+nr)
Продолжительность начисления периода в годах
Относительная величина годовой процентной ставки
Наращенная сумма
Первоначальная сумма

Продолжительность года в днях
Относительная величина годовой процентной ставки
Наращенная сумма
Первоначальная сумма
Продолжительность периода начисления в днях

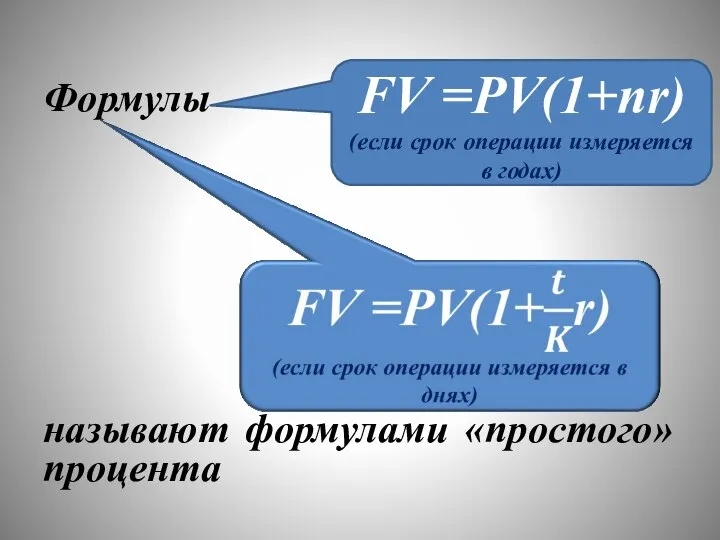
Формулы
называют формулами «простого» процента
FV =PV(1+nr)
(если срок операции измеряется в годах)

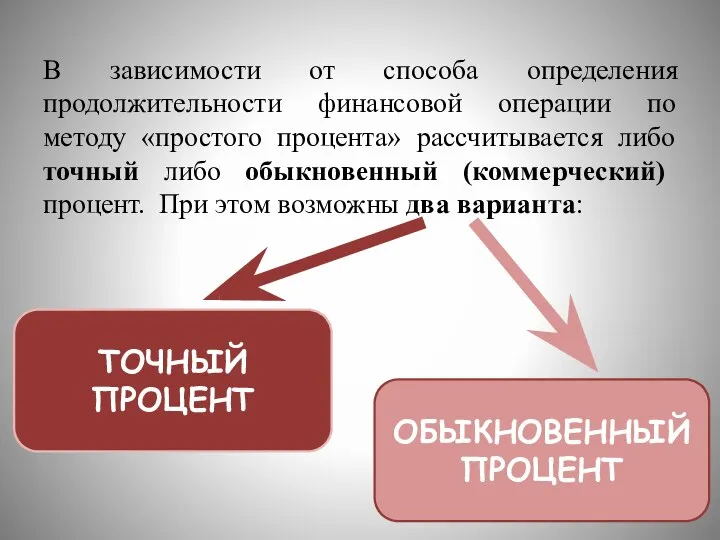
В зависимости от способа определения продолжительности финансовой операции по методу «простого процента» рассчитывается либо точный либо обыкновенный (коммерческий) процент. При этом возможны два варианта:
ТОЧНЫЙ ПРОЦЕНТ
ОБЫКНОВЕННЫЙ ПРОЦЕНТ

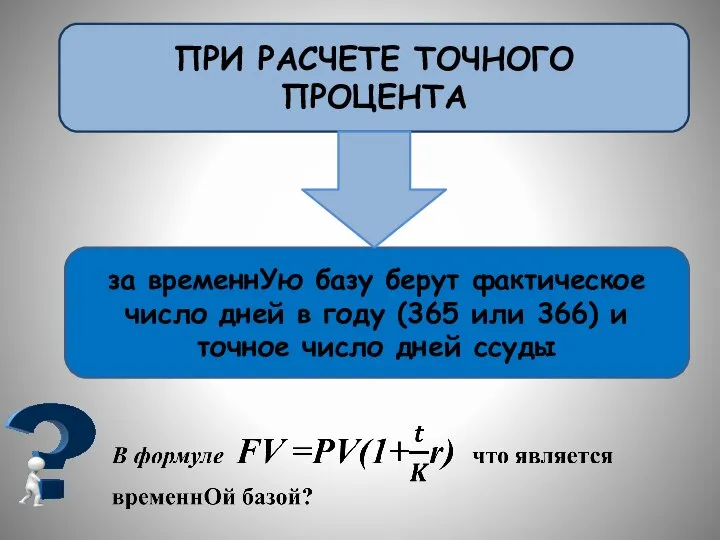
ПРИ РАСЧЕТЕ ТОЧНОГО ПРОЦЕНТА
за временнУю базу берут фактическое число дней в году (365 или 366) и точное число дней ссуды

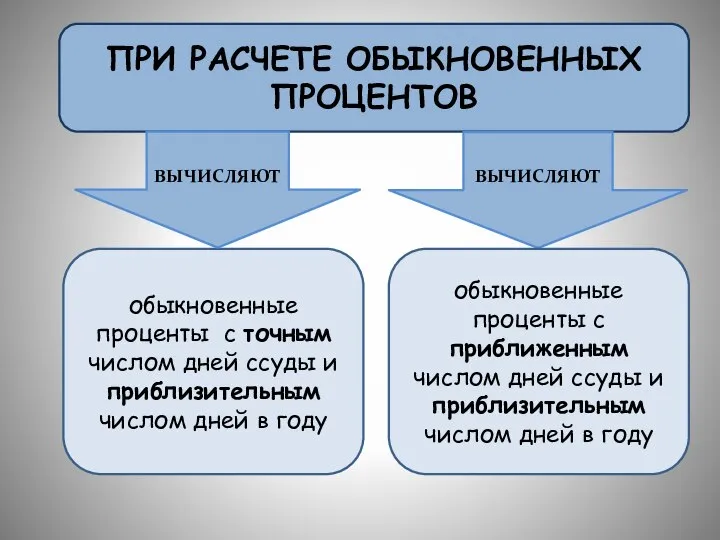
ПРИ РАСЧЕТЕ ОБЫКНОВЕННЫХ ПРОЦЕНТОВ
обыкновенные проценты с точным числом дней ссуды и приблизительным числом дней в году
ВЫЧИСЛЯЮТ
ВЫЧИСЛЯЮТ
обыкновенные проценты с приближенным числом дней ссуды и приблизительным числом дней в году

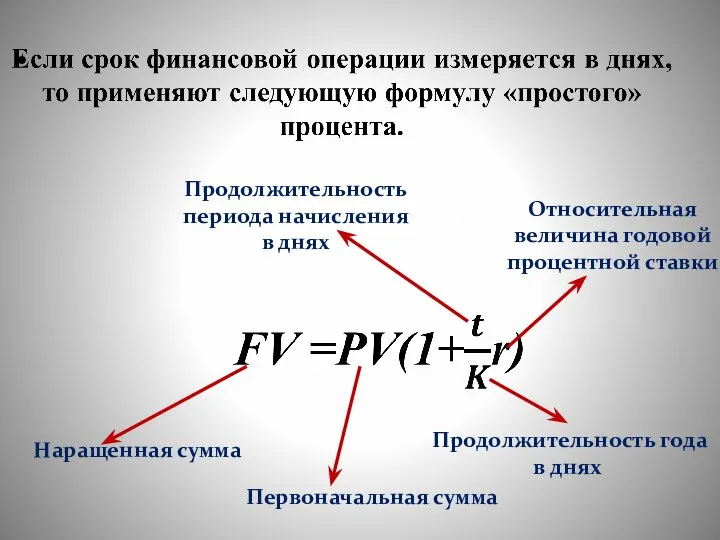
Если срок операции измеряется в днях то t (продолжительность периода начисления в днях) и K (продолжительность года в днях) могут выражены точно и приблизительно

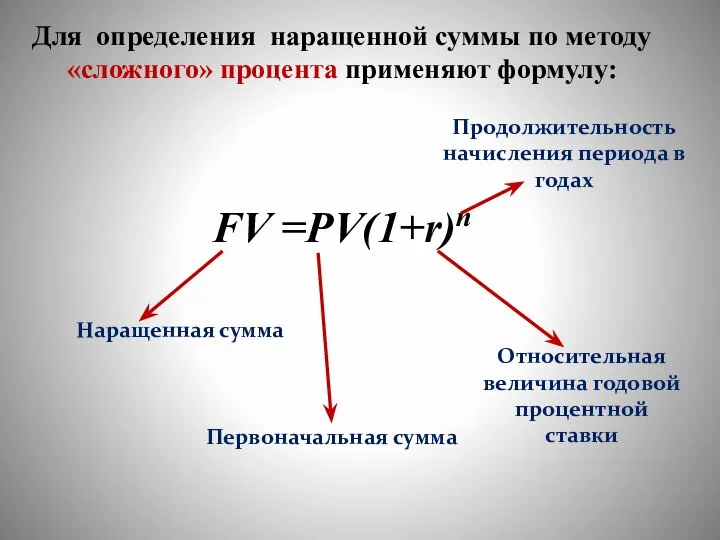
Для определения наращенной суммы по методу «сложного» процента применяют формулу:
FV =PV(1+r)n
Продолжительность начисления периода в годах
Относительная величина годовой процентной ставки
Наращенная сумма
Первоначальная сумма

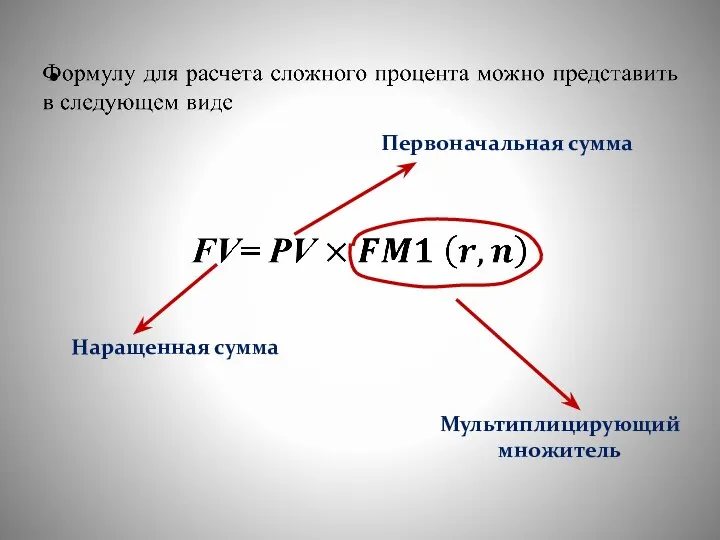
Наращенная сумма
Первоначальная сумма
Мультиплицирующий множитель

Множитель FM1(r, n) = (1 + r)n называется мультиплицирующим множителем для единичного платежа или коэффициентом приращения. И в зависимости от разных комбинаций r и n находится по специальной финансовой таблице.
Экономический смысл множителя FM1(r, n): он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т. п.) через n периодов при заданной процентной ставке r, т. е. он оценивает будущую стоимость одной денежной единицы.

Что понимается под «дисконтированной стоимостью»?
Если посмотреть на этимологию слова discount, то уже в 17 веке оно использовалось в значении «deduction for early payment», что означает «скидка за раннюю оплату».
Таким образом, можно дать следующее определение:
Дисконтирование от английского «discounting» – приведение экономических значений за разные промежутки времени к заданному отрезку времени.

Дисконтированная стоимость – это текущая стоимость будущего денежного потока (т.е. будущий платеж за вычетом «скидки» за быструю оплату)
Дисконтированную стоимость часто называют приведенной стоимостью. Говоря простыми словами, приведенная стоимость – это будущая денежная сумма, приведенная к текущему моменту

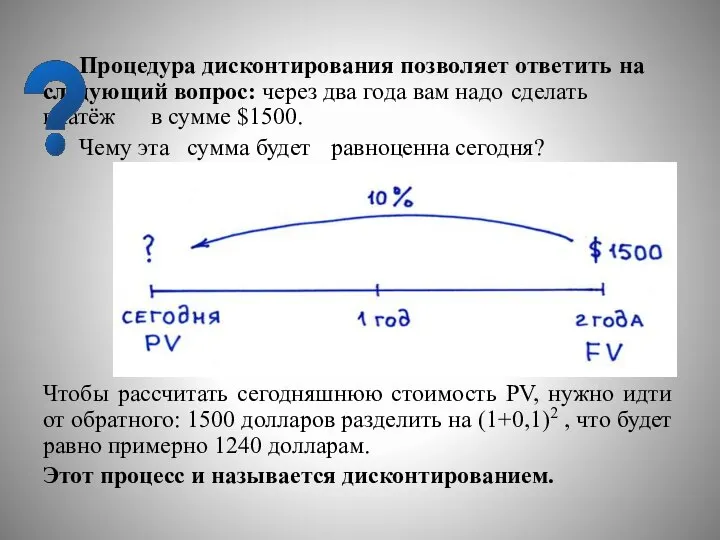
Процедура дисконтирования позволяет ответить на следующий вопрос: через два года вам надо сделать платёж в сумме $1500.
Чему эта сумма будет равноценна сегодня?
Чтобы рассчитать сегодняшнюю стоимость PV, нужно идти от обратного: 1500 долларов разделить на (1+0,1)2 , что будет равно примерно 1240 долларам.
Этот процесс и называется дисконтированием.

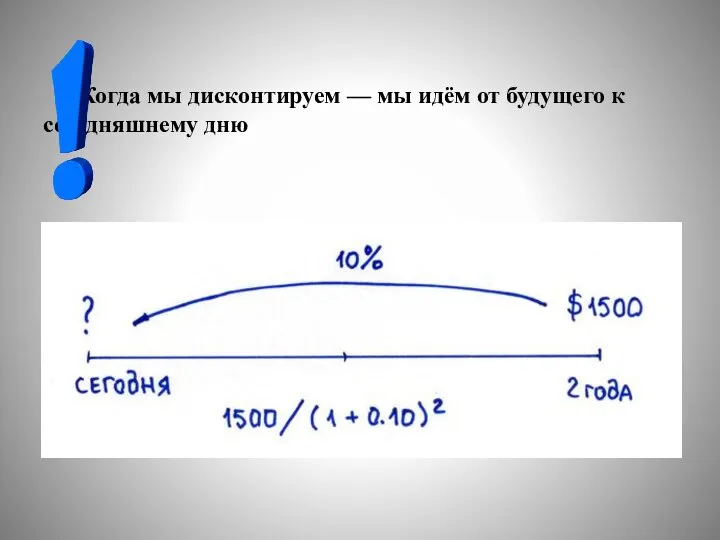
Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню

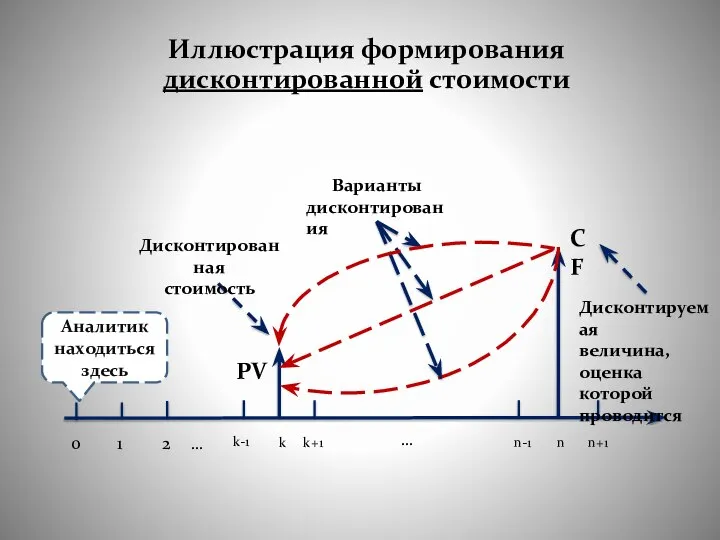
Иллюстрация формирования дисконтированной стоимости
Аналитик находиться здесь
0
1
2
…
k-1
k
k+1
…
n-1
n
n+1
СF
Варианты
дисконтирования
Дисконтированная
стоимость
PV
Дисконтируемая
величина,
оценка которой
проводится

Дисконтированная (приведенная, текущая) стоимость
Доход, планируемый к получению в n-м году
Ставка дисконтирования
Дисконтирующий множитель

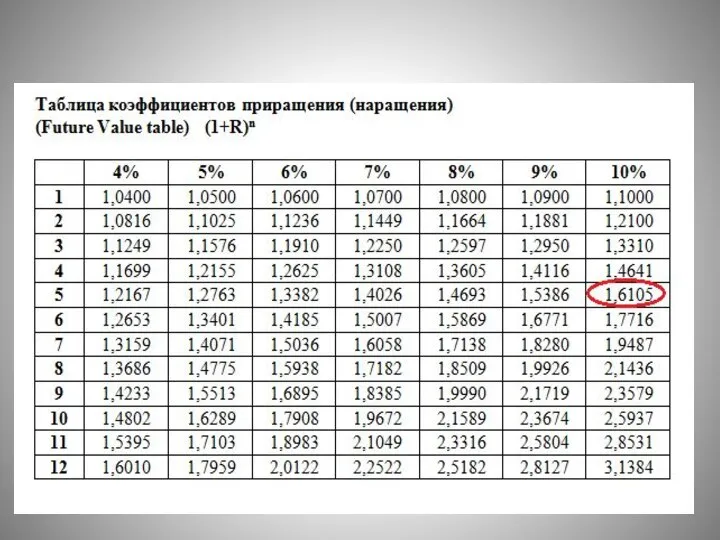
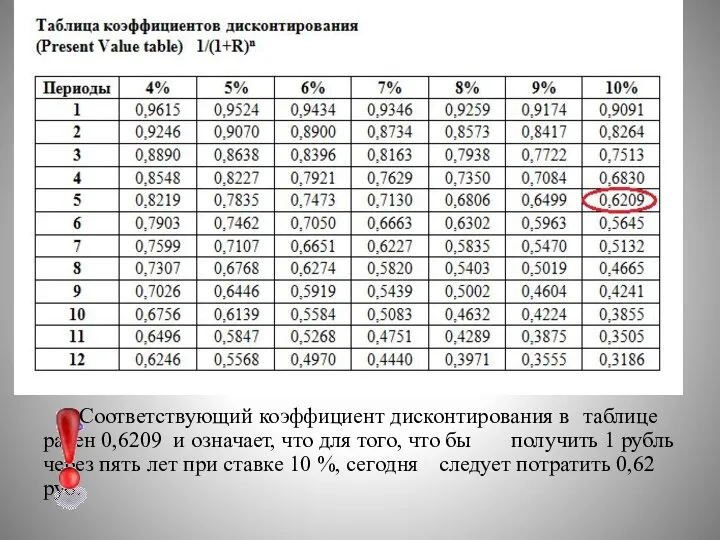
Дисконтирующим множителем для единичного платежа.
В зависимости от величин
r и n
он находится по специальной финансовой таблице

Соответствующий коэффициент дисконтирования в таблице равен 0,6209 и означает, что для того, что бы получить 1 рубль через пять лет при ставке 10 %, сегодня следует потратить 0,62 руб.

ДЕНЕЖНЫЙ ПОТОК
В инвестиционном анализе будущие
денежные суммы, поступающие
в процессе реализации инвестиционного
проекта принято обозначать
CF – (от cash flow- денежный поток)
Поэтому важным является оценка денежного потока CF1, CF2,...... CFn, генерируемых в течение ряда временных периодов в результате реализации какого-либо проекта или функционирования того или иного вида активов.

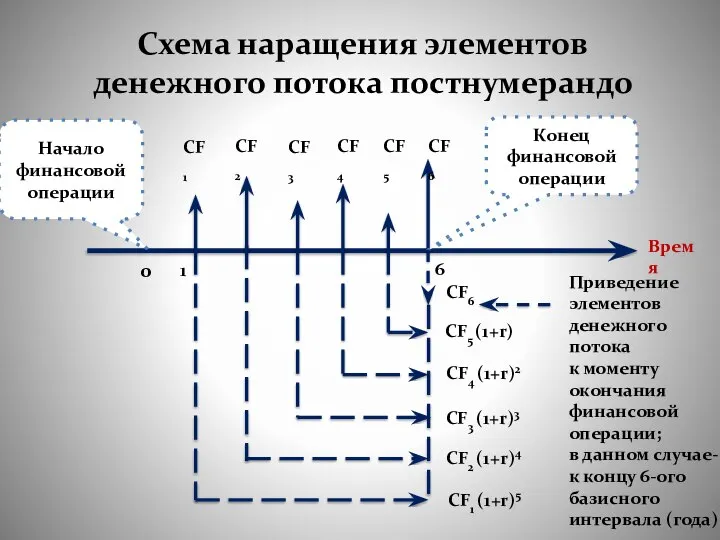
Наращение денежного потока постнумерандо
Представим, что CF1, CF2,...... CFk — совокупность периодических, каждый месяц, денежных взносов в банк на депозит.
Какая сумма будет на счете в конце данной операции?
Простое суммирование потоков CF1, CF2,...... CFk не возможно, поскольку они находятся в разных временных интервалах и не сопоставимы из за разной временнОй ценности денег.
Эта несопоставимость устраняется с помощью наращения по схеме сложных процентов.

Схема наращения элементов денежного потока постнумерандо
Время
6
0
1
Приведение элементов
денежного потока
к моменту окончания
финансовой операции;
в данном случае-
к концу 6-ого базисного
интервала (года)
Конец
финансовой
операции
Начало финансовой операции
CF1
CF2
CF3
CF4
CF5
CF6
CF6
CF5 (1+r)
CF4 (1+r)2
CF3 (1+r)3
CF2 (1+r)4
CF1 (1+r)5

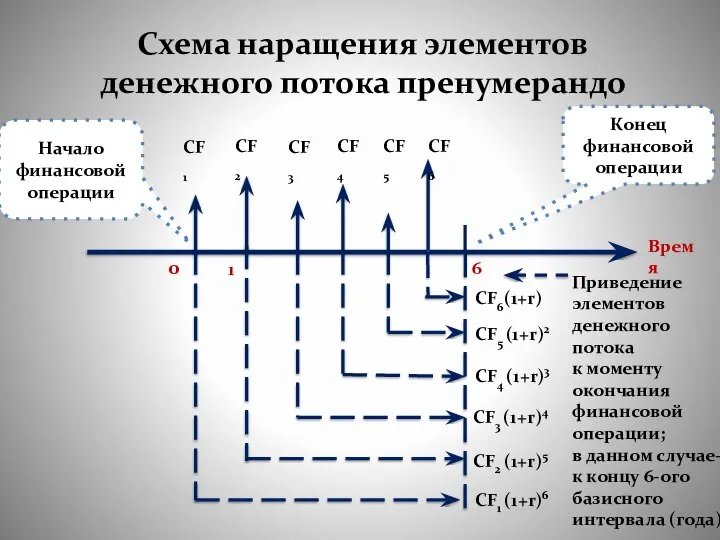
Только после приведения всех потоков в точку 6 их можно просуммировать.
как видно из рисунка, элемент денежного потока CF6 уже находится в конечной точке, поэтому наращения не требуется
элемент денежного потока CF5 находится в конце 5-го периода, а потому по истечении 6-го периода на эту сумму будут начислены проценты по ставке r по схеме сложного процента
элемент денежного потока СF4 требует двукратного начисления,
и т. д.

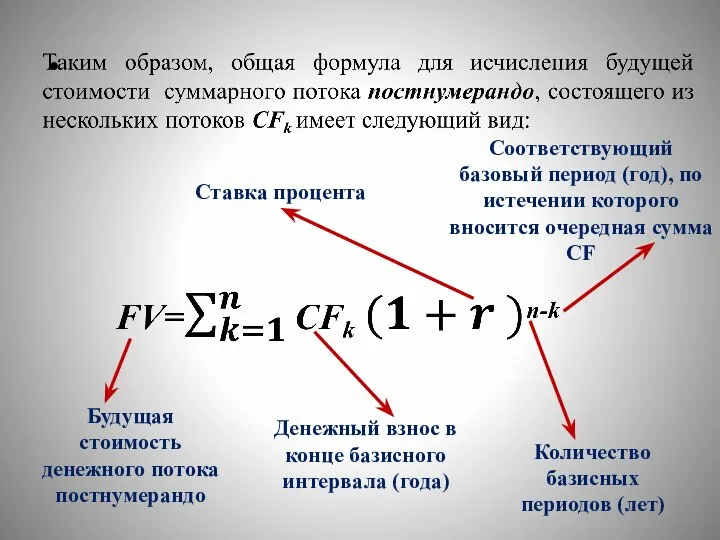
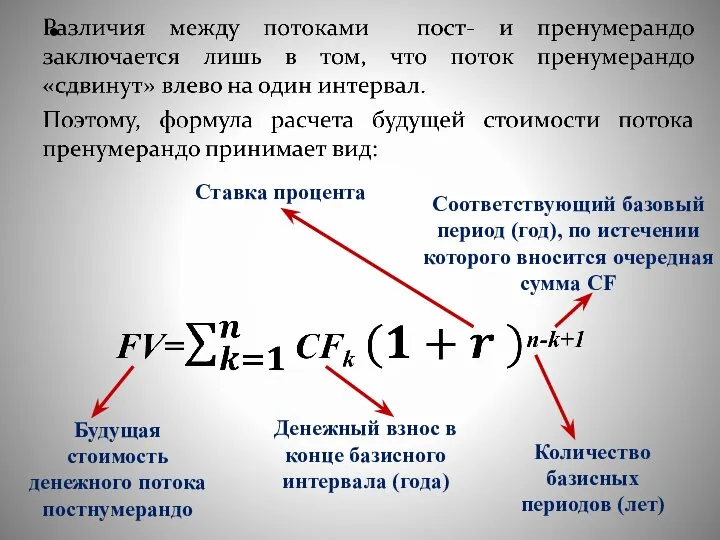
Будущая стоимость денежного потока постнумерандо
Денежный взнос в конце базисного интервала (года)
Ставка процента
Количество базисных периодов (лет)
Соответствующий базовый период (год), по истечении которого вносится очередная сумма CF

Обратная задача подразумевает оценку с позиции будущего момента времени на начало определенного периода.
Пусть имеем исходный денежный поток CF1, CF2, ..., CFn. Например - это совокупность регулярных доходов по ценной бумаге (облигации), которую инвестору предлагают купить.
Перед инвестором встает вопрос: сколько он готов заплатить за возможность обладания данным денежным потоком

Как и в случае наращения элементов денежного очевидно, что простое суммирование элементов потока CFk невозможно, поскольку они находятся в разных временных интервалах.
Эта несопоставимость вновь устраняется с помощью дисконтирования по схеме сложных процентов.

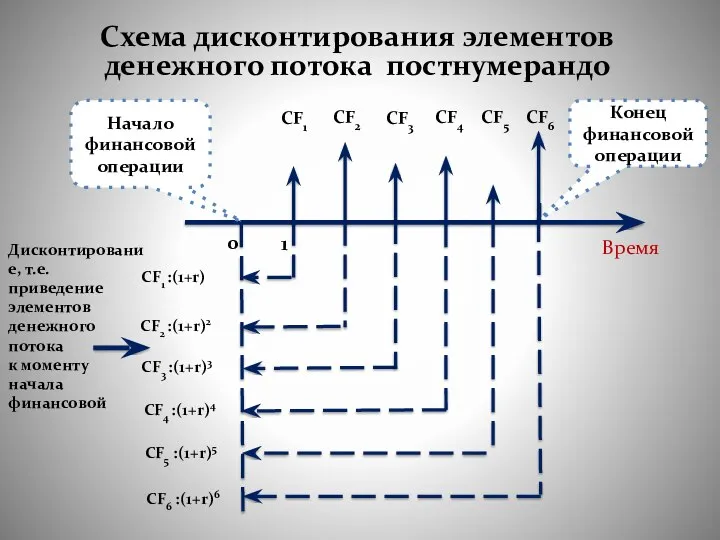
Схема дисконтирования элементов денежного потока постнумерандо
Время
0
1
Дисконтирование, т.е. приведение элементов
денежного потока
к моменту начала
финансовой
Конец
финансовой
операции
Начало финансовой операции
CF1
CF2
CF3
CF4
CF5
CF6
CF1 :(1+r)
CF2 :(1+r)2
CF3 :(1+r)3
CF4 :(1+r)4
CF5 :(1+r)5
CF6 :(1+r)6

Только после приведения всех потоков в точку 0 их можно просуммировать.
как видно из рисунка элемент денежного потока CF1 отдален от точки приведения на один интервал, потому он делится на (1 + r)
элемент денежного потока CF2 отдален двумя интервалами, а потому делится на (1 + r)2
элемент денежного потока CF3 отдален тремя интервалами, а потому делится на (1 + r)3 и т. д.

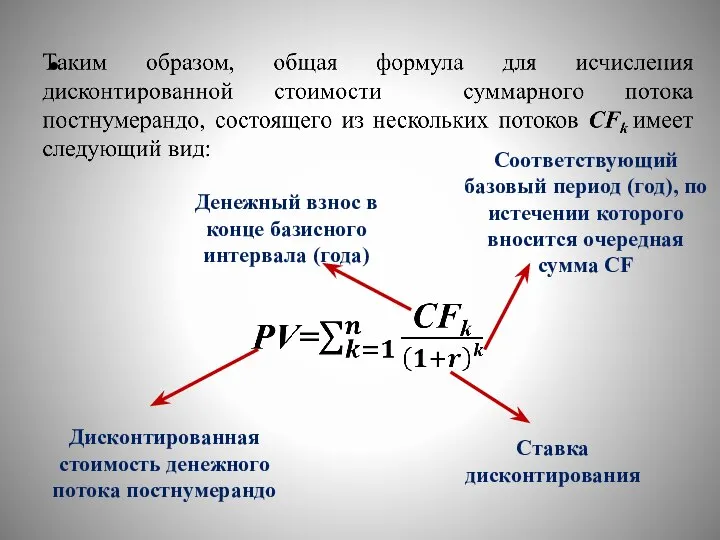
Дисконтированная стоимость денежного потока постнумерандо
Денежный взнос в конце базисного интервала (года)
Ставка дисконтирования
Соответствующий базовый период (год), по истечении которого вносится очередная сумма CF

Схема наращения элементов денежного потока пренумерандо
Время
6
0
1
Приведение элементов
денежного потока
к моменту окончания
финансовой операции;
в данном случае-
к концу 6-ого базисного
интервала (года)
Конец
финансовой
операции
Начало финансовой операции
CF1
CF2
CF3
CF4
CF5
CF6
CF6(1+r)
CF5 (1+r)2
CF4 (1+r)3
CF3 (1+r)4
CF2 (1+r)5
CF1 (1+r)6

Будущая стоимость денежного потока постнумерандо
Денежный взнос в конце базисного интервала (года)
Ставка процента
Количество базисных периодов (лет)
Соответствующий базовый период (год), по истечении которого вносится очередная сумма CF

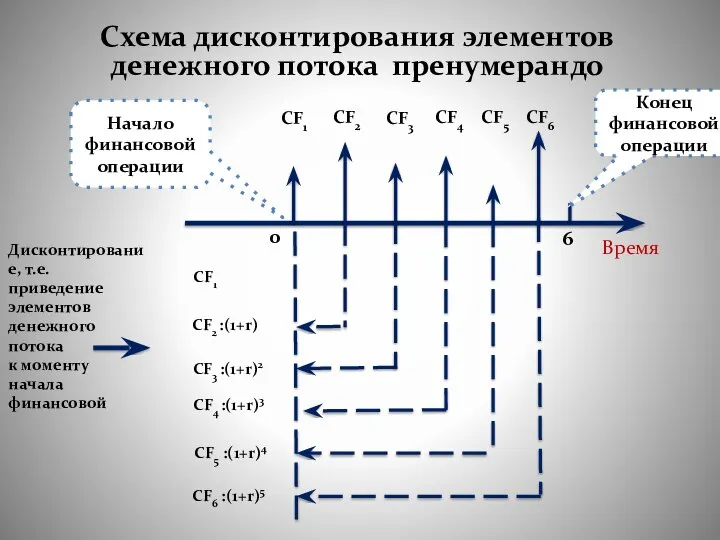
Схема дисконтирования элементов денежного потока пренумерандо
Время
0
Дисконтирование, т.е. приведение элементов
денежного потока
к моменту начала
финансовой
Конец
финансовой
операции
Начало финансовой операции
CF1
CF2
CF3
CF4
CF5
CF6
CF1
CF2 :(1+r)
CF3 :(1+r)2
CF4 :(1+r)3
CF5 :(1+r)4
CF6 :(1+r)5
6