Слайд 2Логические схемы
Логические схемы – схемы, выполняющие операции преобразования: запоминания, пересылки двоичных

битов информации в компьютере
Логический элемент (вентиль) – часть электронной логической схемы, которая выполняет элементарную логическую операцию. К элементарным логическим операциям реализуемым на логических микросхемах относятся операции: и, или, не, и-или, и-не, или-не, и-или-не и другие
Слайд 3Логические схемы
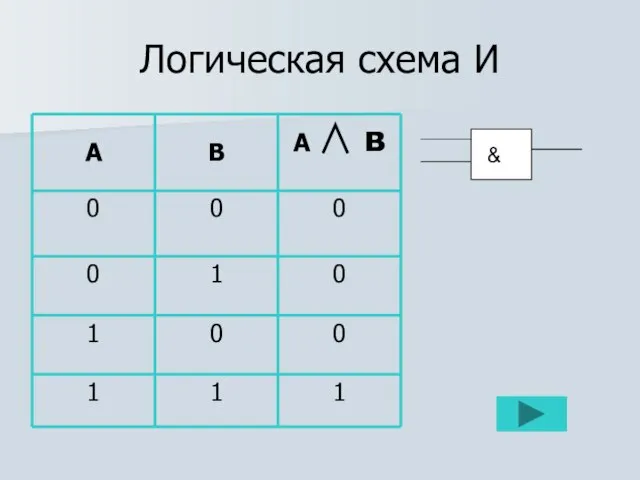
Логический элемент И - конъюнктор.
Х
Y Х&Y
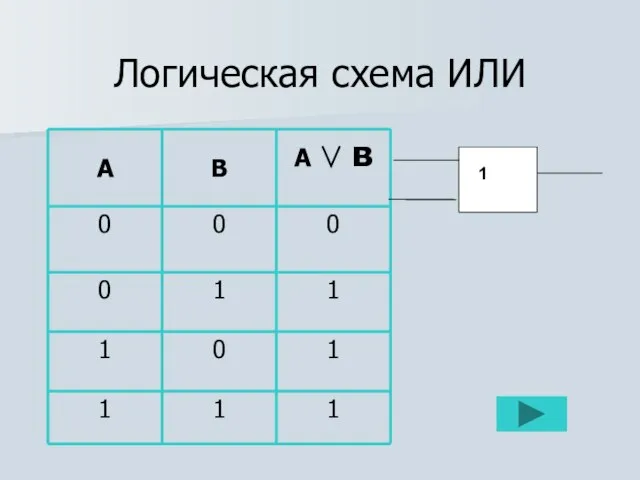
Логический элемент ИЛИ –

дизъюнктор.
X X∨Y
Y
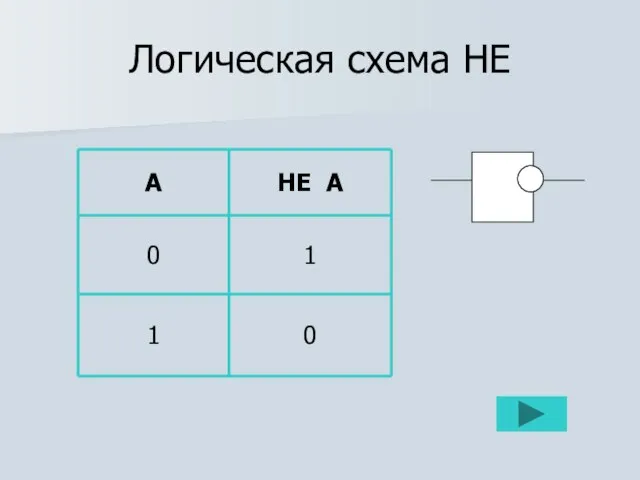
Логический элемент НЕ – инвертор.
Х _
Х
Слайд 7Логические схемы
Рассмотрим реализацию логических элементов через электрические контактные схемы. Контакты обозначены латинскими

буквами.
Цепь с последовательным соединением соответствует логической операции И (конъюнкции).
Физический аналог :
Слайд 8Логические схемы
Цепь с параллельным соединением соответствует логической операции ИЛИ (дизъюнкции).
Логическая операция НЕ
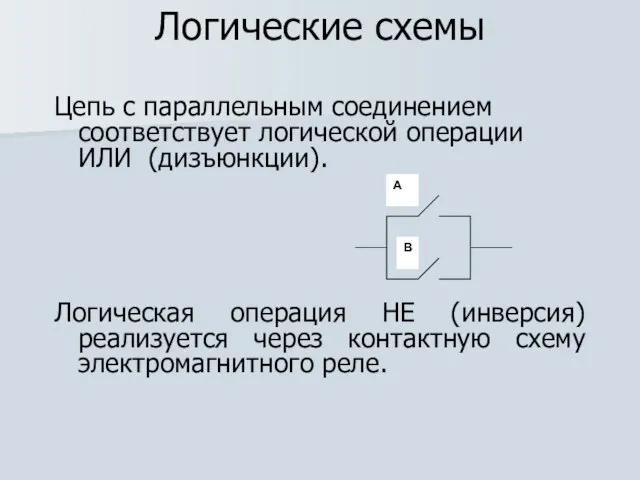
(инверсия) реализуется через контактную схему электромагнитного реле.
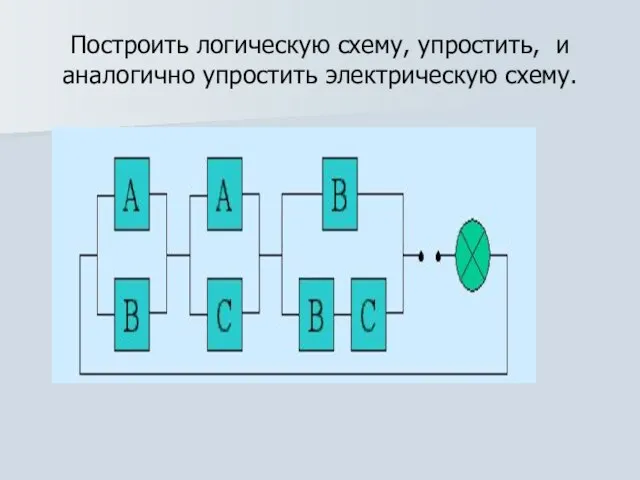
Слайд 9Построить логическую схему, упростить, и аналогично упростить электрическую схему.
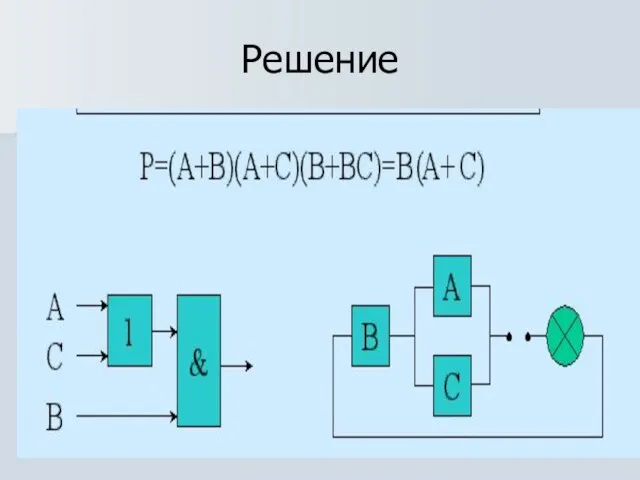
Слайд 10Решение
Логику данного элемента можно записать следующим образом:
А или В =(А v
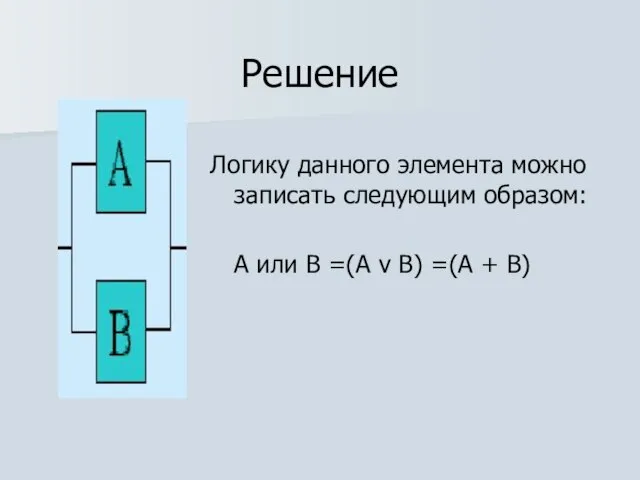
B) =(А + В)
Слайд 11Решение
Логику данного элемента можно записать следующим образом:
А или С =(А v
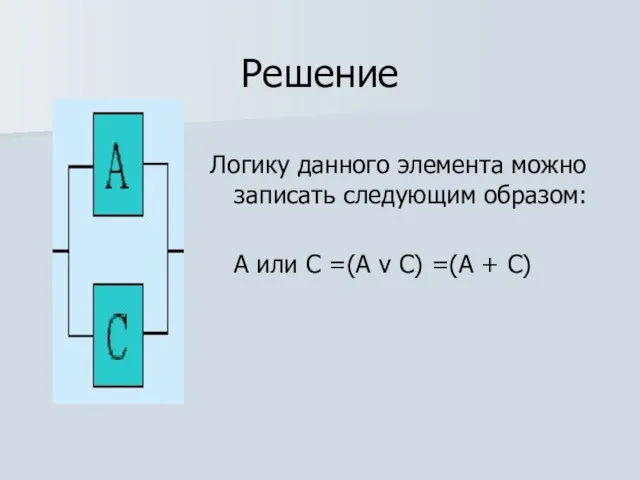
С) =(А + С)
Слайд 12Решение
Логику данного элемента можно записать следующим образом:
В и С =(В ^
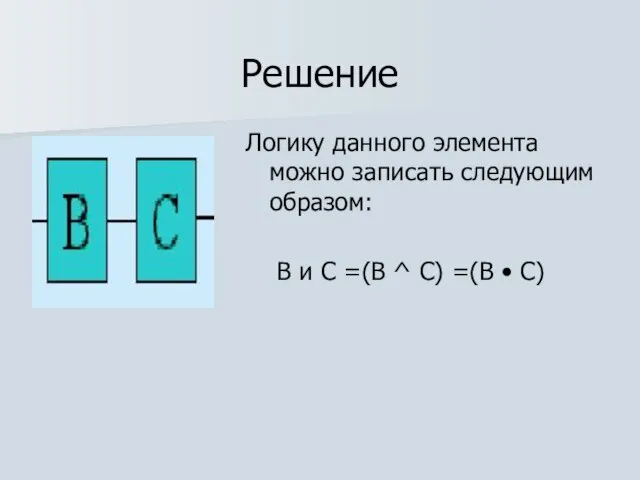
С) =(В • С)
Слайд 13Решение
В выражение:
А или В =(А v B) =(А + В)
подставим А=(В
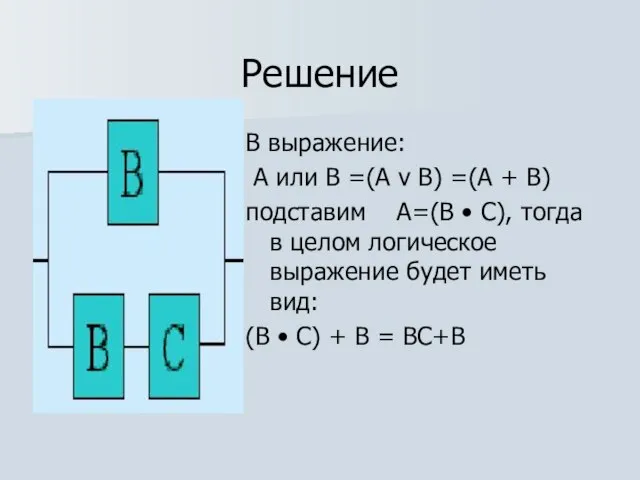
• С), тогда в целом логическое выражение будет иметь вид:
(В • С) + В = ВС+В
Слайд 14И для всей схемы в целом имеем:
(А + В) (А +
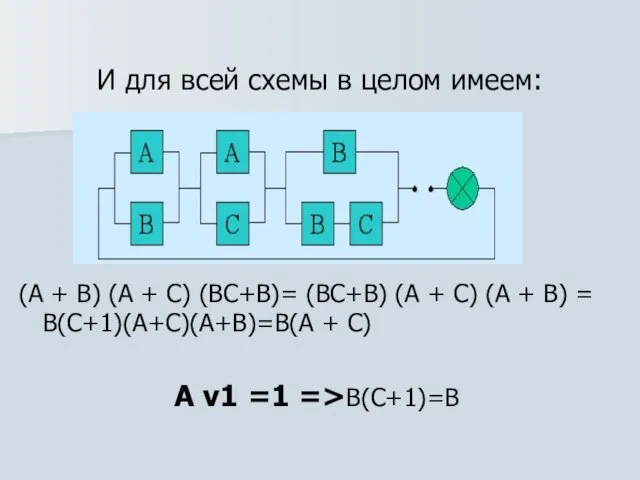
С) (ВС+В)= (ВС+В) (А + С) (А + В) = В(С+1)(А+С)(А+В)=В(А + С)
А v1 =1 =>В(С+1)=В
Слайд 16 Алгебра логики дала в руки конструктора мощное средство разработки, анализа и

совершенствования логических схем. Гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл математического моделирования.
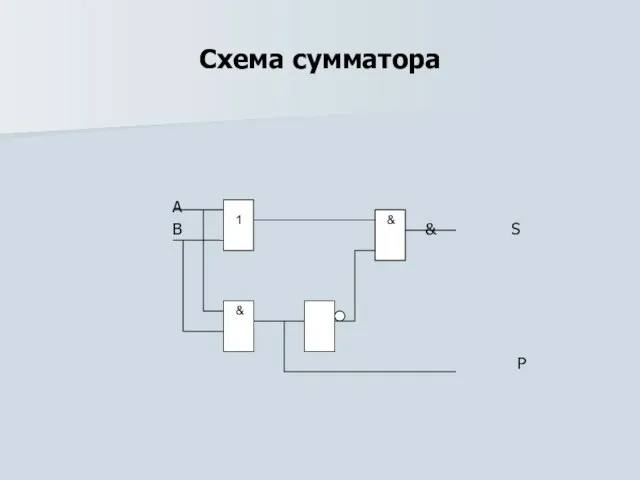
Слайд 17Сумматор –
это электронная логическая схема, выполняющая суммирование двоичных чисел.
В целях

максимального упрощения работы компьютера все многообразие математических операций в процессоре сводится к сложению двоичных чисел. Поэтому главной частью процессора является сумматор, который обеспечивает такое сложение. При сложении двоичных чисел образуется сумма в данном разряде, при этом возможен перенос в старший разряд. Обозначим слагаемые А и В, сумму S и перенос Р. Построим таблицу сложения одноразрядных двоичных чисел с учетом переноса в старший разряд.
Слайд 18Сумматор –
Cоставим булево выражение по этой таблице:
_ _
S = A&B
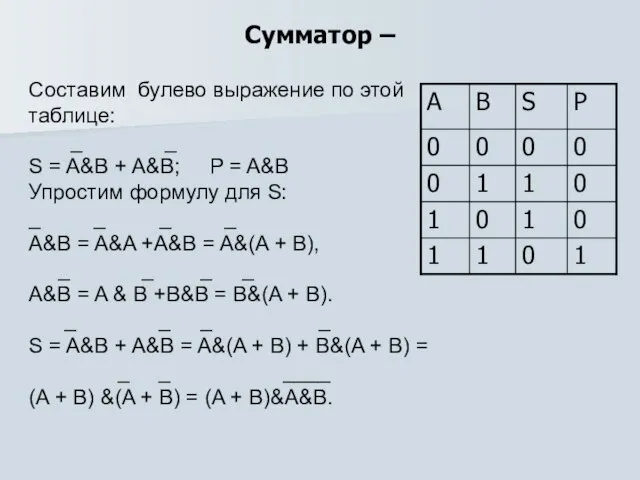
+ A&B; P = A&B
Упростим формулу для S:
_ _ _ _
A&B = A&A +A&B = A&(A + B),
_ _ _ _
A&B = A & B +B&B = B&(A + B).
_ _ _ _
S = A&B + A&B = A&(A + B) + B&(A + B) =
_ _ ____
(A + B) &(A + B) = (A + B)&A&B.
Слайд 20Триггер. Регистры
Триггер – устройство памяти компьютера для хранения одного бита информации.
Это устройство
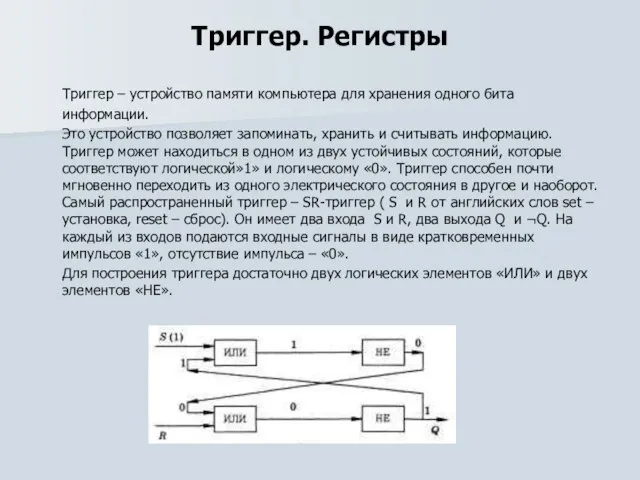
позволяет запоминать, хранить и считывать информацию. Триггер может находиться в одном из двух устойчивых состояний, которые соответствуют логической»1» и логическому «0». Триггер способен почти мгновенно переходить из одного электрического состояния в другое и наоборот. Самый распространенный триггер – SR-триггер ( S и R от английских слов set – установка, reset – сброс). Он имеет два входа S и R, два выхода Q и ¬Q. На каждый из входов подаются входные сигналы в виде кратковременных импульсов «1», отсутствие импульса – «0».
Для построения триггера достаточно двух логических элементов «ИЛИ» и двух элементов «НЕ».
Слайд 21Триггер
При подаче сигнала на вход S триггер переходит в устойчивое единичное состояние.
При

подаче сигнала на вход R триггер сбрасывается в устойчивое нулевое состояние.
При отсутствии входных сигналов триггер сохраняет тот сигнал, который был установлен входным импульсом.
Если на два входа подан сигнал, то появляется неоднозначный результат, поэтому такая комбинация запрещена.















 Презентация на тему Велосипедные походы и безопасность туристов
Презентация на тему Велосипедные походы и безопасность туристов Методы улучшения систем теплоснабжения
Методы улучшения систем теплоснабжения Хозяйство страны. 8 класс
Хозяйство страны. 8 класс Динозавр
Динозавр Значение воинского учета граждан для военной безопасности государства
Значение воинского учета граждан для военной безопасности государства Презентация на тему Царство Растения
Презентация на тему Царство Растения 44 Додаток
44 Додаток Подводный мир
Подводный мир Мультисчета в приложении
Мультисчета в приложении Лес Инвест Трейдинг
Лес Инвест Трейдинг Партнерская программа Станкин - Siemens
Партнерская программа Станкин - Siemens Игрушка Полкан
Игрушка Полкан СD DVD Blue Ray Flash как носители информации
СD DVD Blue Ray Flash как носители информации  Сыбайлас жемқорлық қылмысын жасайтын қылмыскер тұлғасы
Сыбайлас жемқорлық қылмысын жасайтын қылмыскер тұлғасы Оздоровительное и кондиционное плавание
Оздоровительное и кондиционное плавание Устное народное творчество
Устное народное творчество Презентация на тему Модели атомов. Опыт Резерфорда.
Презентация на тему Модели атомов. Опыт Резерфорда.  Презентация на тему Учим дорожные знаки
Презентация на тему Учим дорожные знаки  Тема_1_Предмет_и_социокультурные_функции_философии
Тема_1_Предмет_и_социокультурные_функции_философии Организация производства. Тема 4
Организация производства. Тема 4 Спорт в США
Спорт в США Закрепление письменных навыков сложения и вычитания в пределах 100.
Закрепление письменных навыков сложения и вычитания в пределах 100. Ж
Ж Цели урока – пример уровней оценки
Цели урока – пример уровней оценки Презентация на тему Формирование у детей дошкольного возраста навыков безопасного поведения через ознакомление с правилами доро
Презентация на тему Формирование у детей дошкольного возраста навыков безопасного поведения через ознакомление с правилами доро Инвестиционная политика авиапредприятия и инвестиционное проектирование
Инвестиционная политика авиапредприятия и инвестиционное проектирование Многообразие и значение насекомых в биоценозах
Многообразие и значение насекомых в биоценозах Страховая терминология
Страховая терминология