Математические методы в психологии

Рекомендуемая литература
Ермолаев-Томин, О.Ю Математические методы в психологии. – М., 2013. – 511 с.
Кутейников, А.Н. Математические методы в психологии. – СПб. : Речь, 2008. – 172 с.
Митина, О.В. Математические методы в психологии. Практикум. - М.: Аспект Пресс, 2008. - 238 с.
Наследов, А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. – СПб. : Речь, 2004. – 392 с.
Перевозкина Ю.М, Перевозкин С.Б. «Основы математической статистики в психолого-педагогических исследованиях» в 2 частях. Новосибирск: Изд-во НГПУ, 2014, Ч.1. -115 с., Ч.2. – 242 с.
Сидоренко, Е.В. Методы математической обработки в психологии. – СПб. : Речь, 2002. – 350 с.

Тема 1. Измерение в психологии
История возникновения
Предмет и назначение дисциплины
Измерение в психологии. Взаимоотношение параметров, признаков, показателей и переменных.
Шкалы измерений по С. Стивенсу

В первой четверти XIX в. философ И.Ф. Гербарт (1776-1841) провозгласил психологию наукой, которая должна основываться на опыте метафизики и математики. Правда, он признавал основным психологическим методом наблюдение, а не эксперимент, который присущ, по его мнению, физике. Идеи Гербарта оказали сильнейшее влияние на признанных основоположников экспериментальной психологии – Г. Фехнера и В. Вундта.
И. Ф. Гербарт (1776-1841)

(William Sealy Gosset, 13 июня 1876, Кентербери — 16 октября 1937, Беконсфильд) — известный учёный-статистик, более известный под своим псевдонимом Стьюдент благодаря своим работам по исследованию т. н. распределения Стьюдента.
Родился в Кентербери, у Агнес Сили Видал и полковника Фредерика Госсета. Госсет посещал колледж Винчестер (англ.), а затем прослушал курсы химии и математики в Новом колледже Оксфорда. По окончании университета в 1899 году он поступил на работу на пивоваренный завод Arthur Guinness Son & Co в Дублине.
Гиннесс был передовым предприятием пищевой промышленности, и Госсет мог применить свои знания в области статистики как при варке пива, так и на полях — для выведения самого урожайного сорта ячменя. Госсет приобретал эти знания путём изучения, методом проб и ошибок, проведя два года (1906—1907 гг.) в биометрической лаборатории Карла Пирсона. Госсет и Пирсон были в хороших отношениях, и Пирсон помогал Госсету в математической части его исследований. Так, Пирсон был причастен к публикациям 1908 года (принёсших славу Стьюденту), но придавал мало значения этому открытию. Исследования были обращены к нуждам пивоваренной компании и проводились на малом количестве наблюдений. Биометристы же обычно имели дело с сотнями наблюдений и не испытывали необходимости в развитии методов, основанных на малом их количестве.
Ранее другой исследователь, работавший на Гиннесс, опубликовал в своих материалах сведения, составлявшие коммерческую тайну этой пивоваренной компании. Чтобы предотвратить дальнейшее раскрытие конфиденциальной информации, Гиннесс запретил своим работникам публикацию любых материалов, независимо от содержавшейся в них информации. Это означало, что Госсет не мог опубликовать свои работы под своим именем. Поэтому он избрал себе псевдоним Стьюдент, чтобы скрыть себя от работодателя. Поэтому его самое важное открытие получило название Распределение Стьюдента, иначе бы оно могло называться теперь распределением Госсета.
Госсет практически все свои работы, включая работу «Вероятная ошибка среднего» (англ. The probable error of a mean) опубликовал в журнале Пирсона «Биометрика» под псевдонимом Стьюдент. Первым, кто понял значение работ Госсета по оценке параметров малой выборки, был биолог Рональд Фишер. Госсет написал ему: «Я посылаю вам копию таблиц Стьюдента, поскольку вы, похоже, единственный человек, который когда-либо станет пользоваться ими!» Фишер считал, что Госсет совершил «логическую революцию». По иронии судьбы, t-статистика, благодаря которой знаменит Госсет, была фактически изобретением Фишера. Госсет считал статистику для z = t/√(n−1). Фишер предложил вычислять статистику для t, потому что такое представление укладывалось в его теорию степеней свободы. Фишер также применил распределение Стьюдента в регрессионном анализе.

Определение статистики и связь с психологией и математикой
Термин «статистика» имеет несколько значений:
∙ это совокупность данных и сведений, посвященных какому-либо вопросу, в этом значении он используется во многих международных и национальных изданиях, примером чего может служить «Ежегодник мировой санитарной статистики», «статистика, заболеваемости и смертности»; старое значение слова «статистика», как один из разделов науки об управлении государством, сбор, классификация и обсуждение сведений об обществе и государстве.
∙ это описательные или дистрибутивные характеристики описывающие какую то совокупность данных, по каким то параметрам (средняя, дисперсия и так далее);
статистика (или математическая статистика) это научная дисциплина, изучающая методы сбора и обработки фактов и данных, относящихся к человеческой деятельности и природным явлениям.

Слово «статистика» часто ассоциируется со словом «математика», и связывающее это понятие со сложными формулами, требующими высокого уровня абстрагирования.
Статистика – это, прежде всего, способ мышления, и для ее применения нужно лишь иметь немного здравого смысла и знать основы математики. В нашей повседневной жизни мы, сами о том не догадываясь, постоянно занимаемся статистикой. Хотим ли мы спланировать бюджет, рассчитать потребление бензина автомашиной, оценить усилия, которые потребуются для усвоения какого-то курса, с учетом полученных до сих пор отметок, предусмотреть вероятность хорошей и плохой погоды по метеорологической сводке или вообще оценить, как повлияет то или иное событие на наше личное или совместное будущее, – нам постоянно приходится отбирать, классифицировать и упорядочивать информацию, связывать ее с другими данными так, чтобы можно было сделать выводы, позволяющие принять верное решение.
Все эти виды деятельности мало отличаются от тех операций, которые лежат в основе научного исследования и состоят в синтезе данных, полученных на различных группах объектов в том или ином эксперименте, в их сравнении с целью выяснить черты различия между ними, в их сопоставлении с целью выявить показатели, изменяющиеся в одном направлении, и, наконец, в предсказании определенных фактов на основании тех выводов, к которым приводят полученные результаты. Именно в этом заключается цель статистики в науках вообще, особенно в гуманитарных. В последних нет ничего абсолютно достоверного, и без статистики выводы в большинстве случаев были бы чисто интуитивными и не могли бы составлять солидную основу для интерпретации данных, полученных в других исследованиях.

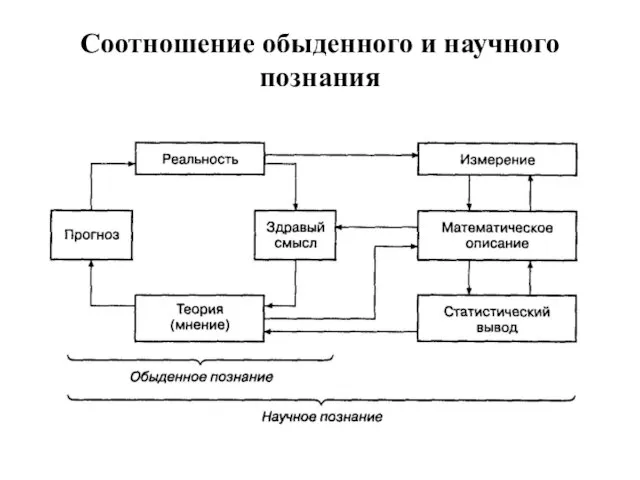
Соотношение обыденного и научного познания

Основные задачи решаемые математическими методами в психологии
Подтверждение экспериментальных данных
Проверка валидности и надежности создаваемых методик
Предсказывание результатов
Создание психологических моделей

Анализ данных на компьютере.
Использование MS Excel
Статистические пакеты: SPSS, STATISTICA.
Особенности подготовки данных для анализа на компьютере.

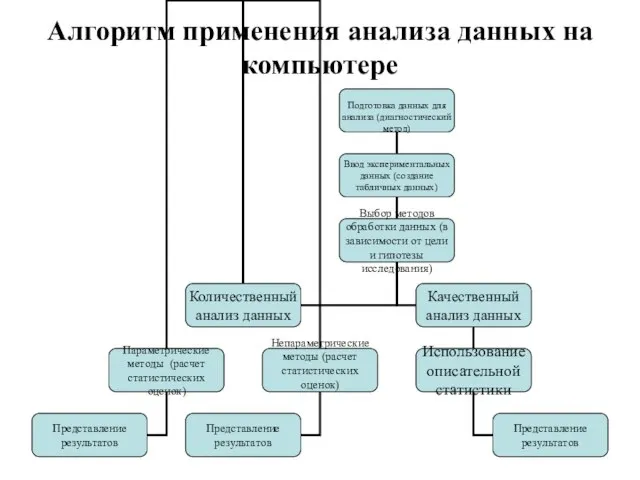
Алгоритм применения анализа данных на компьютере

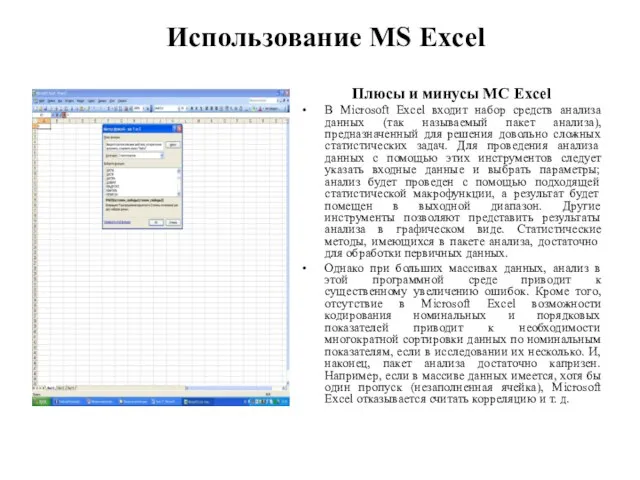
Использование MS Excel
Плюсы и минусы MC Excel
В Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения довольно сложных стати­стических задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической макрофункции, а результат будет помещен в выходной диапазон. Другие инструменты позволяют представить результаты анализа в графическом виде. Статистические методы, имеющихся в пакете ана­лиза, достаточно для обработки первичных данных.
Однако при больших массивах данных, анализ в этой программной среде приводит к существенному увеличению ошибок. Кроме того, отсутствие в Microsoft Excel возможности кодирования номинальных и порядковых показателей приводит к необходимости многократной сортировки данных по номинальным показателям, если в исследовании их несколько. И, наконец, пакет анализа достаточно капризен. Например, если в массиве данных имеется, хотя бы один пропуск (незаполненная ячейка), Microsoft Excel отказывается считать корреляцию и т. д.

Статистические пакеты: SPSS, STATISTICA
STATISTICA for Windows представляет собой интегрированную систему статистического анализа и обработки данных. Она состоит из следующих основных компонент, которые объединены в рамках одной системы:
электронных таблиц для ввода и задания исходных данных, а также специальных таблиц для вывода численных результатов анализа;
мощной графической системы для визуализации данных и результатов статистического анализа;
набора специализированных статистических модулей, в которых собраны группы логически связанных между собой статистических процедур;
специального инструментария для подготовки отчетов;
встроенных языков программирования SCL (STATISTICA Command Language) и STATISTICA BASIC, которые позволяют пользователю расширить стандартные возможности системы.

SPSS
Альтернативное программное обеспечение SPSS включает также все процедуры ввода, отбора и корректировки данных, а также большинство предлагаемых в SPSS статистических методов, что и в STATISTICA. Наряду с простыми методиками статистического анализа, такими как частотный анализ, расчет статистических характеристик, таблиц сопряженности, корреляций, построения графиков, этот модуль включает t-тесты и большое количество других непараметрических тестов, а также усложненные методы, такие как многомерный линейный регрессионный анализ, дискриминантный анализ, факторный анализ, кластерный анализ, дисперсионный анализ, анализ пригодности (анализ надежности) и многомерное шкалирование.

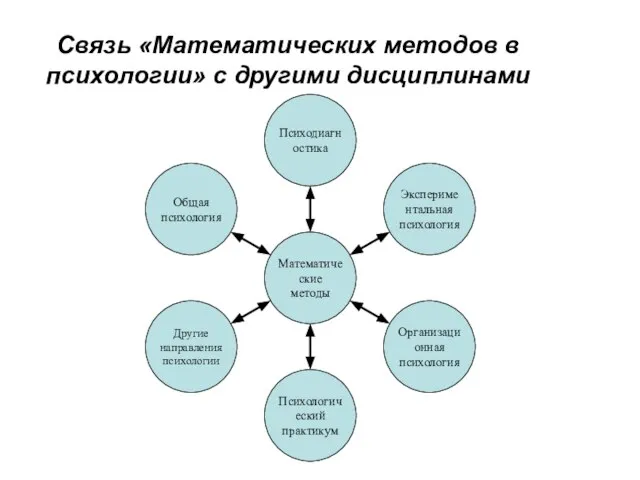
Связь «Математических методов в психологии» с другими дисциплинами

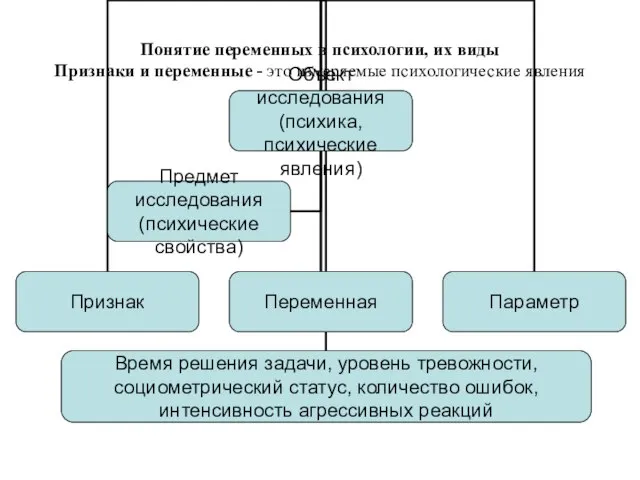
Понятие переменных в психологии, их виды
Признаки и переменные - это измеряемые психологические явления

Измерение — это приписывание объекту числа по определенному правилу. Это правило устанавливает соответствие между измеряемым свойством объекта и результатом измерения — признаком.
Все шкалы условно подразделены на две группы: параметрические и непараметрические.
Шкалы называют параметрическими, если они основаны на нормальном распределении генеральной совокупности (как правило, нормальном) или используют параметры этой совокупности (средние, дисперсии и т.д.).
Шкалы называют непараметрическими, если они не базируются на нормальном типе распределении генеральной совокупности и не использует параметры этой совокупности.
При нормальном распределении генеральной совокупности параметрические шкалы (а они уже составляют параметрические критерии) обладают большей мощностью по сравнению с непараметрическими. Иными словами, они способны с большей достоверностью отвергать нулевую гипотезу, если последняя неверна. Поэтому в тех случаях, когда выборки взяты из нормального распределения генеральных совокупностей, следует отдавать предпочтение параметрическим критериям.
Однако практика показывает, что подавляющее большинство данных, получаемых в психологических экспериментах, не распределены нормально, поэтому применение параметрических критериев в анализе результатов психологических исследований может привести к ошибкам в статистических выводах. В таких случаях непараметрические критерии оказываются более мощными, то есть способными с большей достоверностью отвергать нулевую гипотезу.

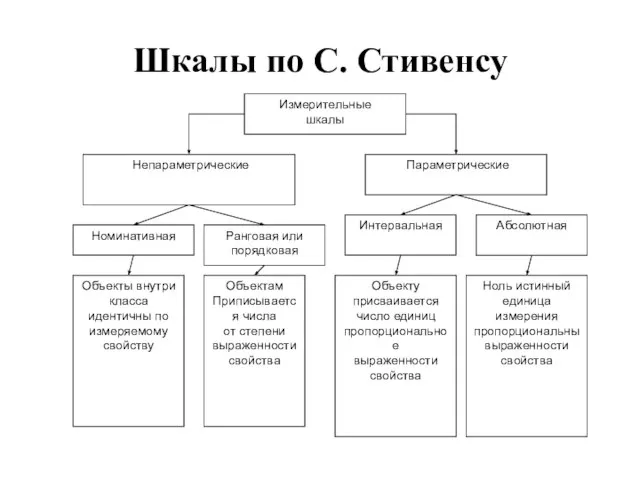
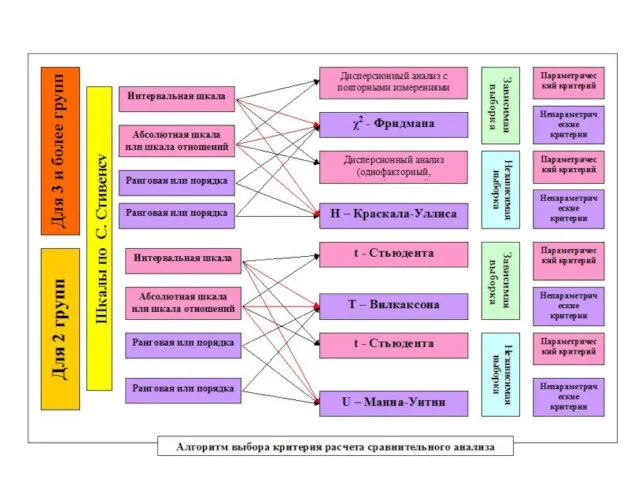
Шкалы по С. Стивенсу

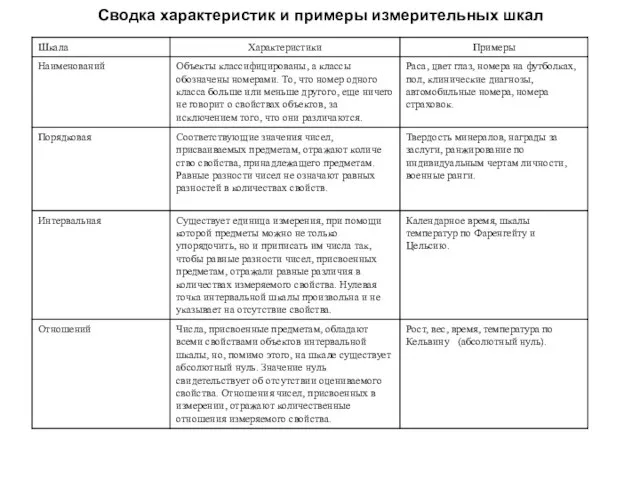
Сводка характеристик и примеры измерительных шкал

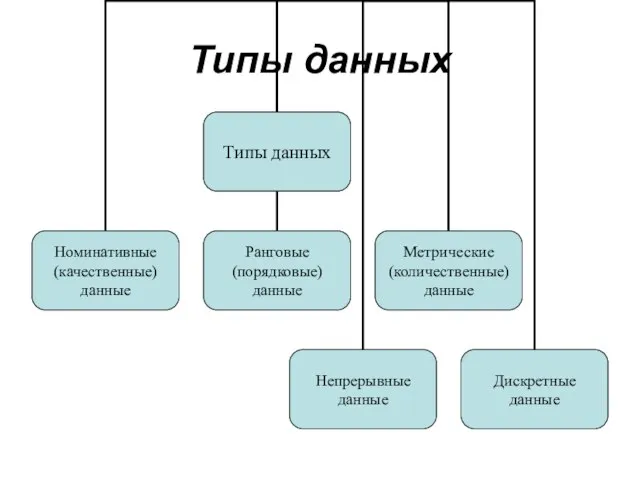
Типы данных

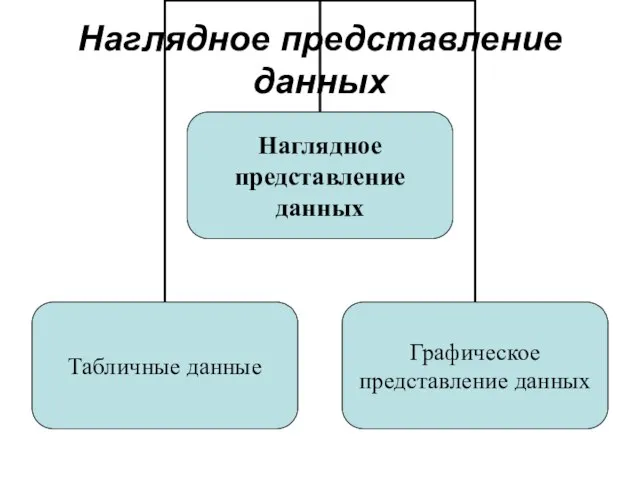
Наглядное представление данных

Графическое представление данных
В самом общем виде диаграммы делятся на:
1. Столбиковые:
Вертикальные;
Горизонтальные;
2. Линейные
Собственно линейные,
Ступенчатые,
Линейные с областями (профили);
3. Точечные (диаграммы рассеянья);
4. Круговые:
Собственно круговая,
Кольцевая,
5. Радиальные:
Звезды;
Лучевые;
6. Диаграммы поверхностей.
7. Комбинированные и др.

Правила графического оформления
Вся структура графика предполагает его чтение слева направо, вертикальные шкалы — снизу вверх.
Чтобы диаграмма не получилась сплющенной или вытянутой, выбирают такой масштаб шкалы, чтобы соотношение высоты к ширине составляли 3 к 5.
На вертикальной шкале необходимо разместить нулевую отметку.
Пороговые точки на шкалах желательно выделить размером или цветом, но если речь идет о временном интервале, предпочтительно не указывать начальной и конечной точек.
Подобрать такой масштаб, чтобы кривые линии резко отличались от прямых, желательно включить в график цифровые данные и изображение формулы, а при необходимости — использовать ясные, полные заголовки и подзаголовки как для самой диаграммы, так и для ее осей.

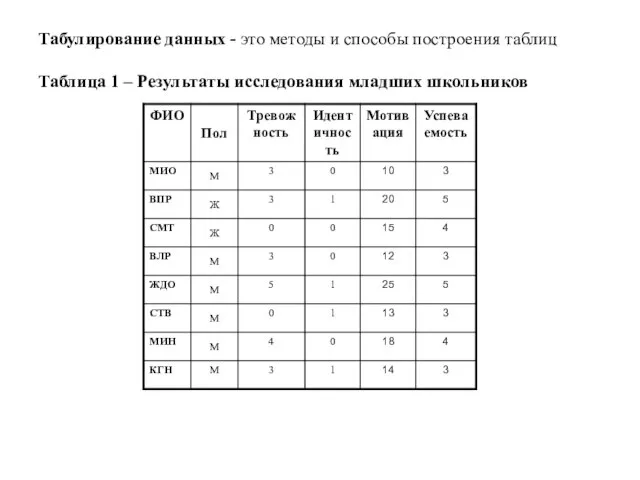
Правила табличного представления первичных данных
Вся структура таблицы предполагает ее чтение слева направо.
В первом столбце предполагается размещение испытуемых.
В последующих столбцах располагаются значения по признакам, полученные после проведения психодиагностической процедуры.

Табулирование данных - это методы и способы построения таблиц
Таблица 1 – Результаты исследования младших школьников

Тема 2. Генеральная совокупность и выборка.
Понятие генеральной совокупности и выборки
Виды вероятностной выборки
Зависимые и независимые выборки
Определение объема выборки при нормальном распределении

Понятие генеральной совокупности и выборки
Генеральной совокупностью – называется всякая большая (конечная или бесконечная) коллекция или совокупность предметов, которые мы хотим исследовать.
Выборка — это часть или подмножество совокупности. Выборка называется репрезентативной если она адекватно отражает свойства генеральной совокупности.
Репрезентативность достигается методом рандомизации, т. е. случайным отбором объектов из генеральной совокупности.

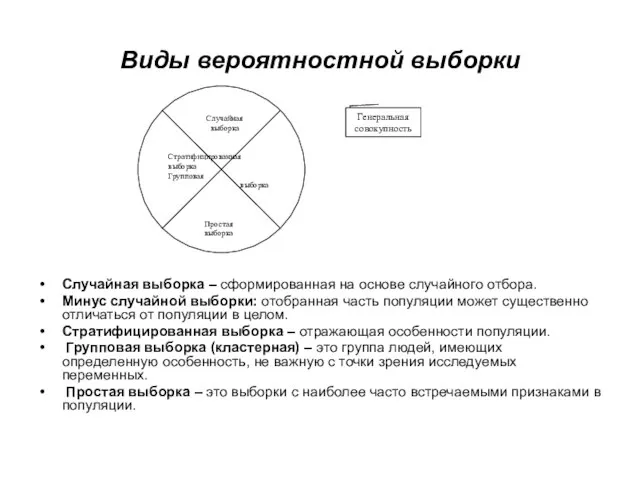
Виды вероятностной выборки
Случайная выборка – сформированная на основе случайного отбора.
Минус случайной выборки: отобранная часть популяции может существенно отличаться от популяции в целом.
Стратифицированная выборка – отражающая особенности популяции.
Групповая выборка (кластерная) – это группа людей, имеющих определенную особенность, не важную с точки зрения исследуемых переменных.
Простая выборка – это выборки с наиболее часто встречаемыми признаками в популяции.

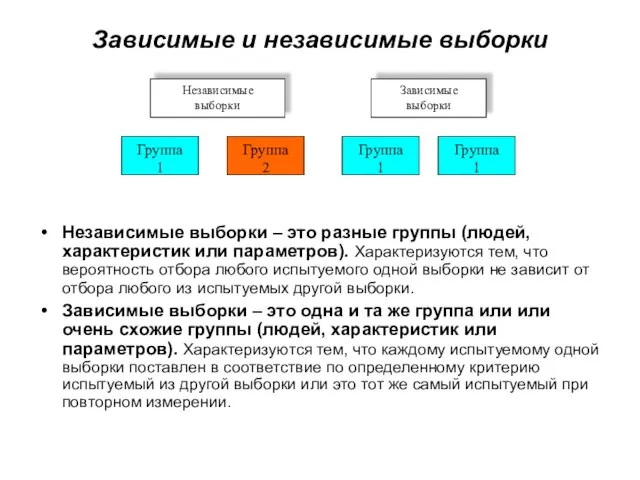
Зависимые и независимые выборки
Независимые выборки – это разные группы (людей, характеристик или параметров). Характеризуются тем, что вероятность отбора любого испытуемого одной выборки не зависит от отбора любого из испытуемых другой выборки.
Зависимые выборки – это одна и та же группа или или очень схожие группы (людей, характеристик или параметров). Характеризуются тем, что каждому испытуемому одной выборки поставлен в соответствие по определенному критерию испытуемый из другой выборки или это тот же самый испытуемый при повторном измерении.

Объем выборки вычисляют, ориентируясь на несколько параметров:
1. Задачи и методы исследования. Это критерий, которым иногда можно ограничиться, решая вопрос об объеме выборки. Так, например, факторный анализ наиболее адекватен, когда выборка составляет не менее 100 случаев (испытуемых, показателей).
2. Однородность генеральной совокупности. Чем более однородна выборка, тем меньший объем выборки будет достаточным для исследования.
Вероятность ошибки (уровень статистической значимости). Данный показатель говорит о степени нашей уверенности в полученном результате.
Предельная ошибка репрезентативности выборки (или кратко: «ошибка выборки»). Эта статистическая величина (обозначается греческой буквой «дельта» — ∆) показывает долю отклонения показателя, полученного в выборочной совокупности, от показателя, который получили бы, сделав измерение на всей генеральной совокупности.
5. Совместное использование вероятности ошибки и предельной ошибки репрезентативности выборки. Как ни запутанно это может звучать, но существует понятие «вероятности ошибки в ошибке выборки». Это означает, что можно ошибиться в допускаемой погрешности. На самом деле всегда есть риск ошибиться в прогнозе события, даже если этим событием является ошибка.

Объем выборки – определяется численностью входящих в нее элементов. Объем выборки зависит от целей и методов исследования, от гомогенности генеральной совокупности, от принимаемой исследователем погрешности.
Гомогенной или однородной называется совокупность, все характеристики которой присущи каждому ее элементу;
Гетерогенной или неоднородной называется совокупность, характеристики которой сосредоточены в отдельных подмножествах элементов.
Объем выборки для нормального распределения определяется по формуле:
где
n — объем выборки;
t — табулированное значение абсциссы для кривой нормального распределения, определяемое желаемой точностью оценки (для наиболее распространенных p = 0,95 t = 1,96; для p = 0,99 t = 2,58);
Δ — предельная репрезентативность выборки (обычно задается исследователем в пределах от 10% до 1% погрешности соответственно);
σ — дисперсия признака в генеральной совокупности.

По схеме испытаний – выборки могут быть независимые и зависимые.
По объему выборки делят на малые и большие.
К малым относят выборки, в которых число элементов n ≤ 30.
Понятие большой выборки не определено, но большой считается выборка в которой число элементов > 200 и средняя выборка удовлетворяет условию 30≤ n≤ 200.
Это деление условно. Малые выборки используются при статистическом контроле известных свойств уже изученных совокупностей.
Большие выборки используются для установки неизвестных свойств и параметров совокупности.

Тема 3.
Способы представления данных в психологии
Представление данных.
Понятие о квантилях.
Понятие о рангах. Процедура ранжирования.
Табулирование данных.
Графическое представление данных.

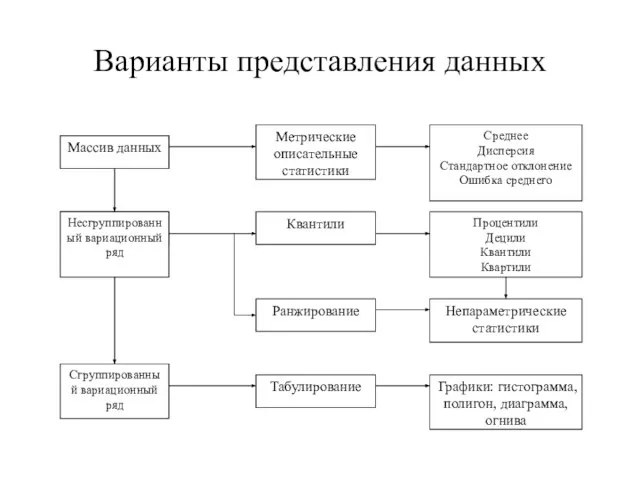
Представление данных в психологии бывает в виде:
Массив данных – первичные результаты измерения искомых параметров сводятся в одну таблицу.
Несгруппированный вариационный ряд – упорядочение всех значений переменной от минимального до максимального.
Сгруппированный вариационный ряд – вариационный ряд сворачивают, указывая все полученные значения однократно, а в соседнем столбце указывают частоту, с которой встречается данная оценка

Варианты представления данных

Меры положения – квантили
Квантиль — это точка на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на две группы с известным соотношением их численности
Процентиль (Percentiles) — это 99 точек — значений признака (Р1 ..., Р99), которые делят упорядоченное (по возрастанию) множество наблюдений на 100 частей, равных по численности.
Дециль - это 9 точек — значений признака (D1 ..., D9), которые делят упорядоченное (по возрастанию) множество наблюдений на 10 частей, равных по численности.
Квинтель - это 4 точки — значений признака (К1 ..., К4), которые делят упорядоченное (по возрастанию) множество наблюдений на 5 частей, равных по численности.
Квартиль - это 3 точки — значений признака (Q1 ..., Q3), которые делят упорядоченное (по возрастанию) множество наблюдений на 4 части, равных по численности.

Нахождение процентиля
Процентили указывают на относительное положение индивида в выборке стандартизации.
Р-й процентиль представляет собой точку, ниже которой лежит Р % процентов всех наблюдений.
Формула
Pp = L + pn – (cum f) ,
f
где L – фактически нижняя граница единичного интервала оценок, содержащего частоту pn;
cum f - накопленная к L частота (до данного интервала);
f – частота оценок в интервале, содержащем частоту pn

Задача: Преподаватель предложил 125 учащимся контрольное задание, состоящее из 40 вопросов. В качестве оценки теста выбиралось количество вопросов, на которые были получены правильные ответы. Найти 25-й процентиль
Нахождение интервала:
Найти между какими значениями в разряде оценок лежит накопленная pn частота (31.25 лежит между 28 и 29 значениями).
Определить сколько единиц составляет интервал, и разделить пополам (между 28 и 29 лежит 1 / 2 = 0,5).
Прибавить к каждому значению интервала результат второго шага (28 + 0,5 = 28,5 и 29 + 0,5 = 29,5)
Таким образом, искомый интервал лежит между 28,5 и 29,5, а его фактически нижняя граница составляет L = 28,5.

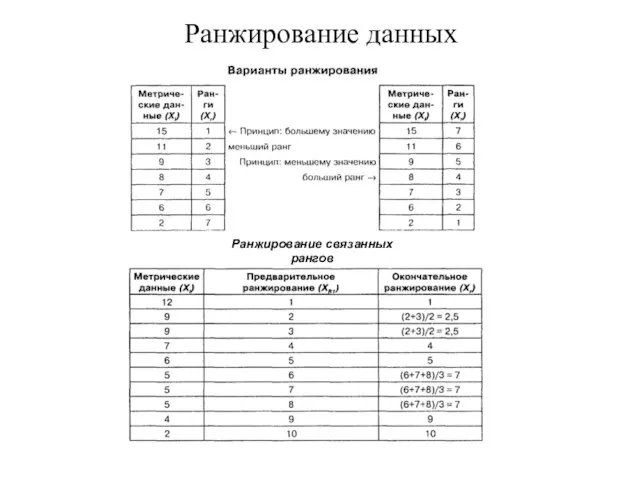
Ранговый порядок
Ранжирование – это приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства
Установите для себя и запомните порядок ранжирования. Вы можете ранжировать испытуемых по их «месту в группе»: ранг 1 присваивается тому, у которого наименьшая выраженность признака, и далее — увеличение ранга по мере увеличения уровня признака. Или можно ранг 1 присваивать тому, у которого 1-е место по выраженности данного признака (например, «самый быстрый»). Строгих правил выбора здесь нет, но важно помнить, в каком направлении производилось ранжирование.
Соблюдайте правило ранжирования для связанных рангов, когда двое или более испытуемых имеют одинаковую выраженность измеряемого свой­ства. В этом случае таким испытуемым присваивается один и тот же, средний ранг. Например, если вы ранжируете испытуемых по «месту в группе» и двое имеют одинаковые самые высокие исходные оценки, то обоим присваивает­ся средний ранг 1,5: (1+2)/2 = 1,5. Следующему за этой парой испытуемому присваивается ранг 3, и т. д.

Ранжирование данных
Ранжирование связанных рангов

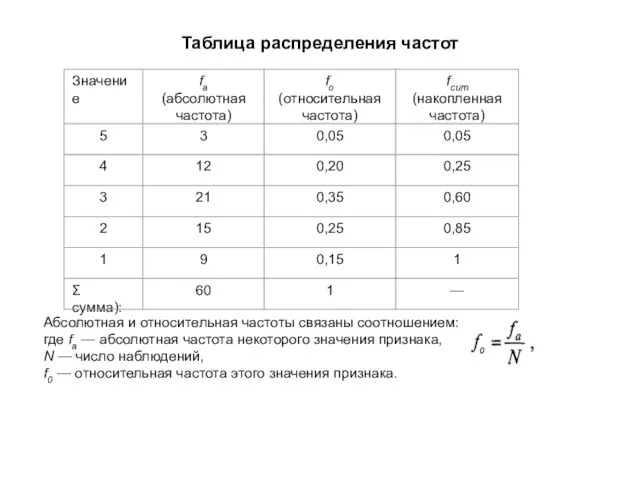
Распределение частот
Абсолютная частота распределения (fa ) - называется частота. указывающая, сколько раз встречается каждое значение
Относительная частотах распределения (fо) – называется частота, указывающая долю наблюдений, приходящихся на то или иное значение признака (f0 = fa / N)
Накопленная частота (fсum) – это частота показывающая, как накапливаются частоты по мере возрастания значений признака.
Сгруппированная частота – это частота сгруппированная по разрядам или интервалам значений признака.

Таблица распределения частот
Абсолютная и относительная частоты связаны соотношением:
где fa — абсолютная частота некоторого значения признака,
N — число наблюдений,
f0 — относительная частота этого значения признака.

Этапы построения распределения сгруппированных частот
Уточнение лимитов (крайних значений интервала) – производится округление лимитов - min и max значений: реальные лимиты max = 67и min = 32, уточненные лимиты max = 70 и min = 30.
Определение размаха: мах – мин = 70-30 = 40
Выбор желаемой ширины интервала разрядов l - наиболее удобной шириной интервала разрядов в является l = 5.
Определение числа разрядов. Размах делится на интервал разряда: 40/5 = 8, получаем число разрядов — 8.
Расчет границ интервалов, посредством прибавления к нижней границе ширину интервала.
Подсчет абсолютной, относительной и накопленной частот

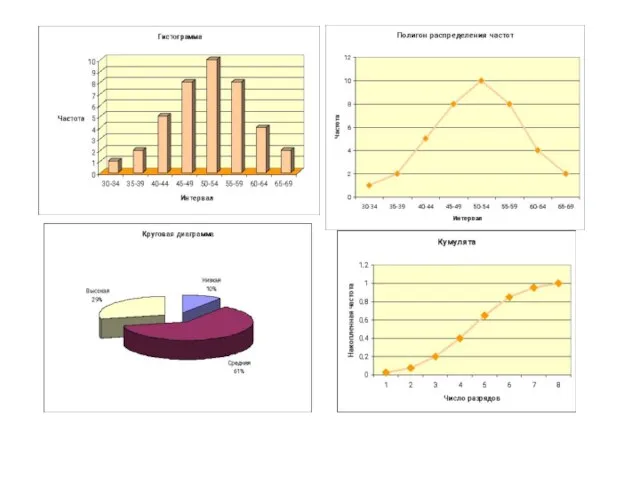
Графическое представление
Гистограмма – это последовательность столбцов, каждый из которых опирается на один раздельный интервал, а высота столбца отражает количество случаев.
Вариационная кривая – линия соединяющая точки, соответствующие середине каждого разрядного интервала и частоте.
Полигон распределения – вариационная кривая с перпендикуляром линий до горизонтальной оси в середине каждого интервала.
Полигон накопленных частот (кумулята) – на оси ординат откладывают значения суммы всех случаев лежащих в данном интервале, так и всех предыдущих интервалов. Сглаженная линия описывает все эти значения.
Огива (процентильная кривая) – сглаженная линия, у которой по оси абсцисс (х) откладывают значения процентов (процентилей), а на оси ординат (у) – значения показателей.
Диаграмма – отражение в долевом отношении частот на круге.

Тема 4. Меры центральной тенденции
Определение меры центральной тенденции;
Мода;
Медиана;
Среднее;
Выбор и особенности мер центральной тенденции.
Графическое соотношение среднего, моды, медианы

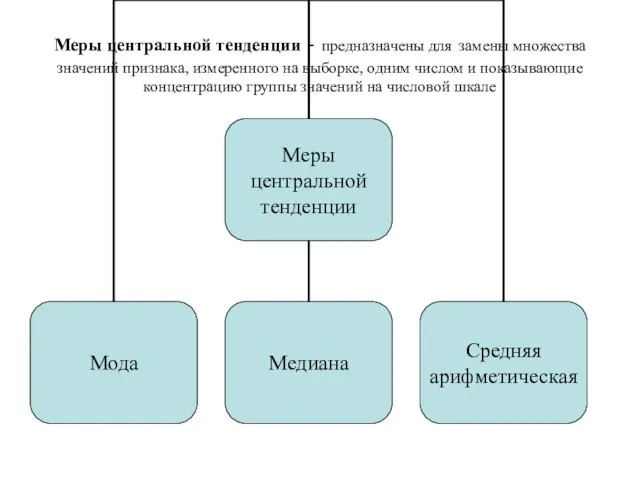
Меры центральной тенденции - предназначены для замены множества значений признака, измеренного на выборке, одним числом и показывающие концентрацию группы значений на числовой шкале

Мода (Mode) — это такое значение из множества измерений, которое встречается наиболее часто.
Если все значения в группе встречаются одинаково часто, то считают, что у данной выборки моды нет (3, 7, 4, 5, 2, 8, 1, 6 - Мо = 0).
Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным (3, 7, 4, 5, 7, 8, 7, 6 - Мо = 7).
Когда два соседних значения встречаются одинаково часто и чаще, чем любое другое значение, мода есть среднее этих двух значений (3, 7, 4, 6, 7, 6, 8, 7, 6 - Мо = 6,5).
Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у такой группы есть две моды, и распределение называют бимодальным (3, 7, 3, 5, 7, 3, 7, 6, 7 - Мо = 7; Мо = 3).
Если в группе несколько значений, встречаются наиболее часто, при этом их частота может различаться, тогда выделяют наибольшую моду и локальные моды и такое распределение называют полимодальным (3, 7, 3, 5, 7, 3, 7, 6, 7, 10, 10. Наибольшая: Мо = 7; локальные: Мо = 3, Мо = 10).

Медиана (Median) — это такое значение признака, которое делит упорядоченное множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая — больше.
Первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию.
Если данные содержат нечетное число значений (8, 9, 10, 13, 15), то медиана есть центральное значение, т. е. Md= 10.
Если данные содержат четное число значений (5, 8, 9, 11), то медиана есть точка, лежащая посередине между двумя центральными значениями, т. е. М/=(8+9)/2 = 8,5.

Среднее (Mean) (М — выборочное среднее, среднее арифметическое) — определяется как сумма всех значений измеренного признака, деленная на количество суммированных значений.
Если к каждому значению переменной прибавить одно и то же число с, то среднее увеличится на это число (уменьшится на это чис­ло, если оно отрицательное).
Если каждое значение переменной умножить на одно и то же число с, то среднее увеличится в с раз (уменьшится в с раз, если делить на с).
Сумма всех отклонений от среднего равна нулю.

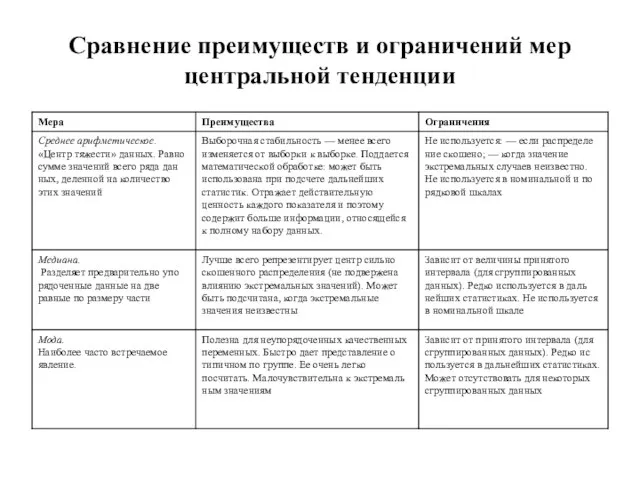
Выбор и особенности мер центральной тенденции
Для номинативных данных единственной подходящей мерой центральной тенденции является мода.
В малых группах мода нестабильна.
Для метрических и порядковых данных наиболее подходящей мерой являются медиана и средняя арифметическая.
На медиану не влияет величины очень больших и очень малых значений
На величину среднего влияет каждое значение, оно чувствительно к «выбросам» — экстремально малым или большим значениям переменной.
Наиболее устойчива к выбросам средняя гармоническая , при расчете которой используются обратные величины.
Если распределение симметричное и унимодальное, то мода, средняя и медиана совпадают.

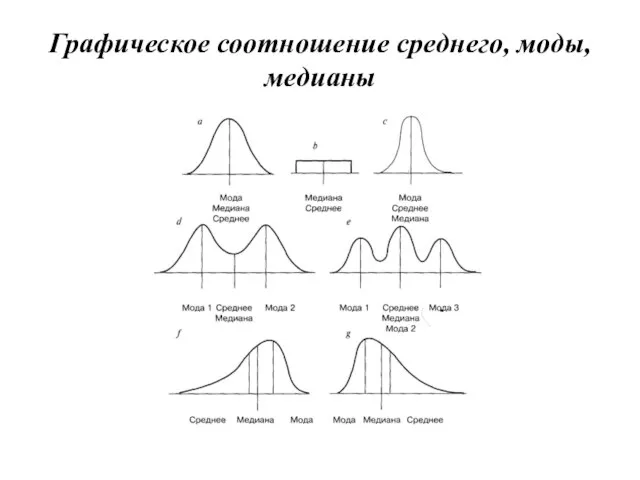
Графическое соотношение среднего, моды, медианы

Сравнение преимуществ и ограничений мер центральной тенденции

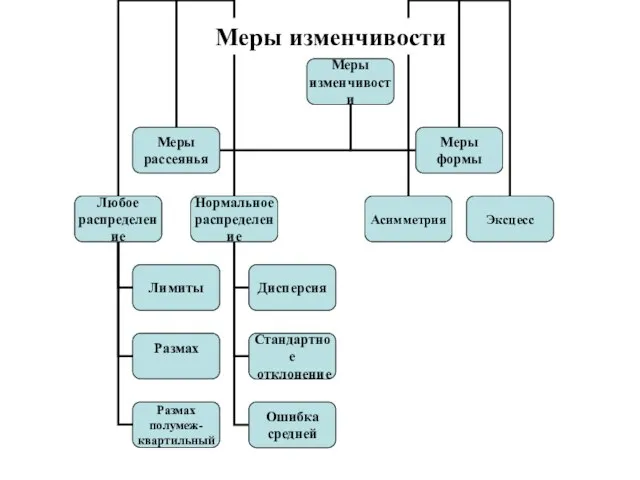
Тема 5. Меры изменчивости
Понятие меры изменчивости
Лимиты. Размах вариации и его разновидности.
Дисперсия и ее свойства.
Стандартное отклонение.
Асимметрия и эксцесс.

Меры изменчивости

Меры рассеяния
независящие от распределения
Лимиты – это характеристики, определяющие верхнюю (max) и нижнюю (min) границы значений показателя.
Размах (Range) — это разность максимального и минимального значений: R = max – min.
Размах это очень неустойчивая мера изменчивости, на которую влияют любые возможные «выбросы».
Более устойчивыми являются разновидности размаха: размах от 10 до 90-го процентиля R = Р90 – Р10 или полумежквартильный размах:

Меры рассеяния
характеризующие нормальное распределение
Дисперсия (Variance) — мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего:
Свойства дисперсии:
1. Если значения измеренного признака не отличаются друг от друга (равны между собой) — дисперсия равна нулю. Это соответствует отсутствию изменчивости в данных.
2. Прибавление одного и того же числа к каждому значению переменной не меняет дисперсию.
3. Умножение каждого значения переменной на константу с изменяет дисперсию в с раз.
4. При объединении двух выборок с одинаковой дисперсией, но с разными средними значениями дисперсия увеличивается.

Расчет дисперсии

Меры рассеяния
характеризующие нормальное распределение
Стандартное отклонение (Std. deviation) (сигма, среднеквадратическое отклонение) — положительное значение квадратного корня из дисперсии, говорит о том, на сколько могут значимо отклоняться, изменяющиеся данные :
Ошибка среднего значения (error of mean) - среднеарифметическое значение среднеквадратичного отклонения, она говорит о том, на сколько могут отклониться данные при повторном исследовании:

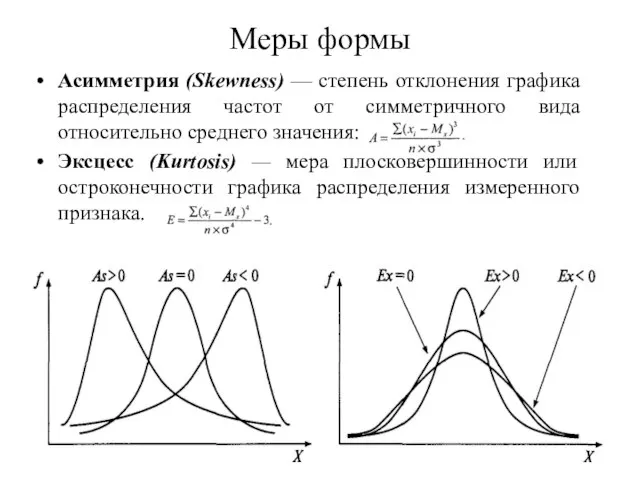
Меры формы
Асимметрия (Skewness) — степень отклонения графика распределения частот от симметричного вида относительно среднего значения:
Эксцесс (Kurtosis) — мера плосковершинности или остроконечности графика распределения измеренного признака.

Тема 6. Стандартизация данных
Понятие стандартизации данных.
Основные формы стандартизации.
z-преобразование данных.

Стандартизация (англ. standard нормальный) — унификация, приведение к единым нормативам процедуры и оценок теста.
Различают две формы стандартизации
В первом случае под С. понимаются обработка и регламентация процедуры проведения, унификация инструкции, бланков обследования, способов регистрации результатов, условий проведения обследования, характеристика контингентов испытуемых.
Во втором случае под С. понимается преобразование нормальной (или искусственно нормализованной) шкалы оценок в новую шкалу, основанную уже не на количественных эмпирических значениях изучаемого показателя, а на его относительном месте в распределении результатов в выборке испытуемых.

Преобразование первичных оценок в новую шкалу
Центрирование – это линейная трансформация величин признака, при котором средняя величина распределения становится равной нулю (М ±σ – нормативный диапазон).
Нормирование - это переход к другому масштабу (единицам) измерения, называемый z-преобразованием данных. z-преобразование данных — это перевод измерений в стандартную Z-шкалу со средним Mz = 0 и Dz (или σ z) = 1.
Этапы перехода к другому масштабу
Для переменной, измеренной на выборке, вычисляют среднее по выборке, индивидуальный показатель (или среднее каждого испытуемого) Мх, стандартное отклонение σх.
Все значения переменной хi пересчитываются по формуле:
Перевод в новую шкалу осуществляется путем умножения каждого z-значения на заданную сигму и прибавления среднего:
Известные шкалы: IQ (среднее 100, сигма 15); Т-оценки (среднее 50, сигма 10); 10-балльная — стены (среднее 5,5, сигма 2) и др.

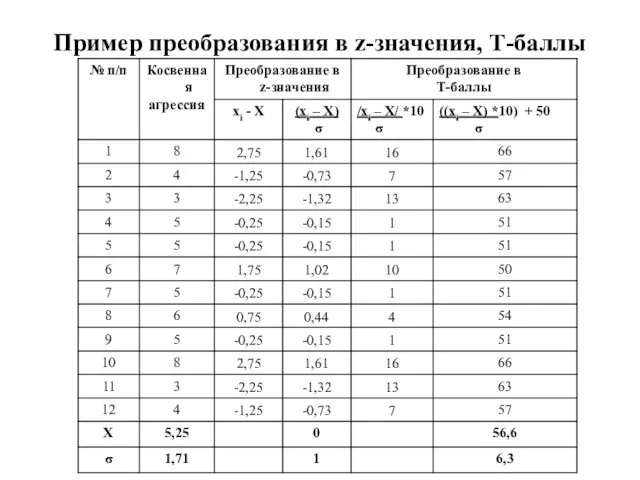
Пример преобразования в z-значения, Т-баллы

Тема 7. Теоретические распределения, используемые при статистических выводах
Нормальное распределение
Единичное нормальное распределение и его свойства
Соответствия между диапазонами значений и площадью под кривой
Проверка нормальности распределения

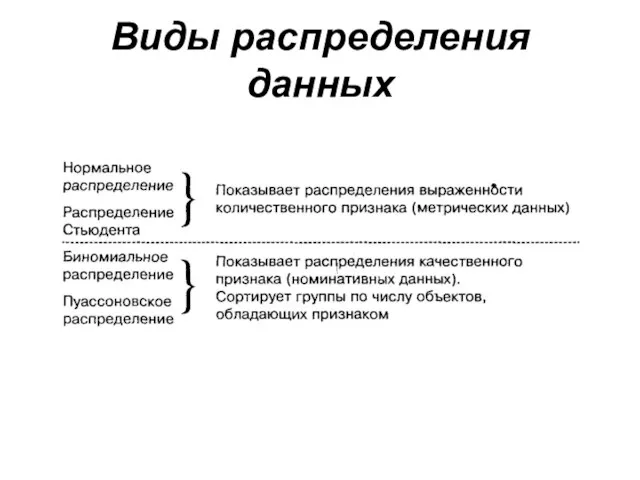
Виды распределения данных

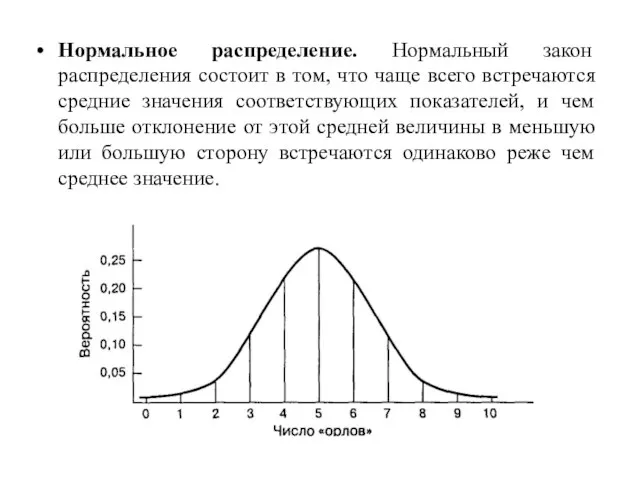
Нормальное распределение. Нормальный закон распределения состоит в том, что чаще всего встречаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины в меньшую или большую сторону встречаются одинаково реже чем среднее значение.

Единичное нормальное распределение и его свойства
Если применить z-преобразование ко всем возможным измерениям свойств, все многообразие нормальных распределений может быть сведено к одной кривой. Тогда каждое свойство будет иметь среднее 0 и стандартное отклонение 1. Это и есть единичное нормальное распределение, которое используется как стандарт — эталон.

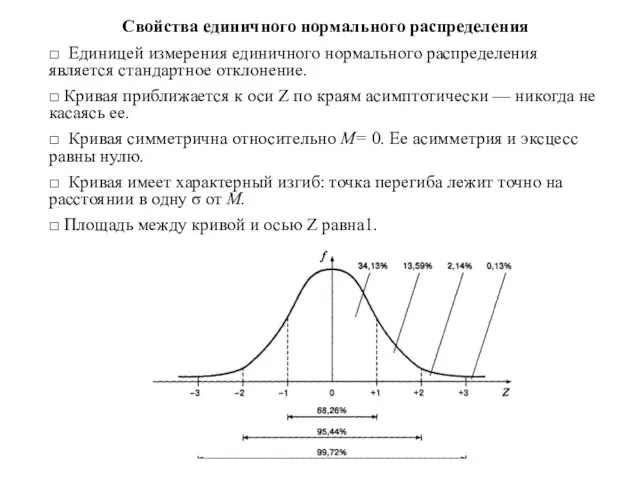
Свойства единичного нормального распределения
□ Единицей измерения единичного нормального распределения является стандартное отклонение.
□ Кривая приближается к оси Z пo краям асимптотически — никогда не касаясь ее.
□ Кривая симметрична относительно М= 0. Ее асимметрия и эксцесс равны нулю.
□ Кривая имеет характерный изгиб: точка перегиба лежит точно на расстоянии в одну σ от М.
□ Площадь между кривой и осью Z paвна1.

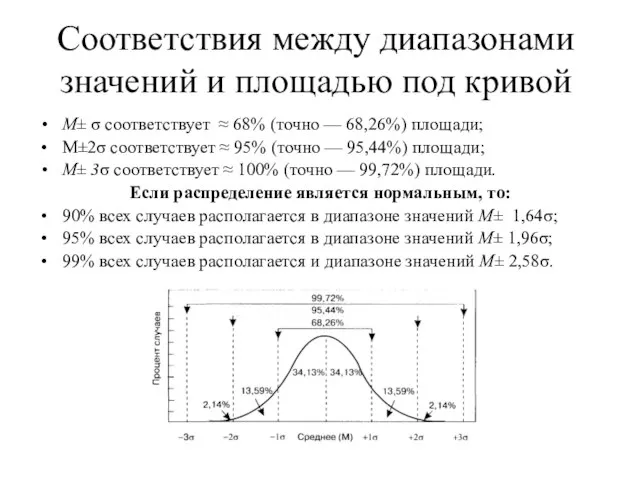
Соответствия между диапазонами значений и площадью под кривой
М± σ соответствует ≈ 68% (точно — 68,26%) площади;
М±2σ соответствует ≈ 95% (точно — 95,44%) площади;
М± 3σ соответствует ≈ 100% (точно — 99,72%) площади.
Если распределение является нормальным, то:
90% всех случаев располагается в диапазоне значений М± 1,64σ;
95% всех случаев располагается в диапазоне значений М± 1,96σ;
99% всех случаев располагается и диапазоне значений М± 2,58σ.

Проверка нормальности распределения
1. Нормальность распределения результативного признака можно проверить путем расчета показателей асимметрии и эксцесса по Н.А. Плохинскому, которые определяется по формулам:
где |A| - абсолютная величина асимметрии;
mA – стандартная ошибка асимметрии.
где |Е| - абсолютная величина эксцесса;
mЕ – стандартная ошибка
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз. Все значения tA и tE не превышают свою ошибку репрезентативности в три раза, из чего можно заключить, что распределение признака не отличается от нормального.
,
,

2. Еще одним из критериев проверки на нормальность - является критерий Колмагорова-Смирнова.
Он позволяет оценить вероятность того, что данная выборка принадлежит генеральной совокупности с нормальным распределением.
Вероятность р ≤ 0,05, распределение отличается от нормального.
Вероятность р > 0,05, распределение соответствует нормальному.

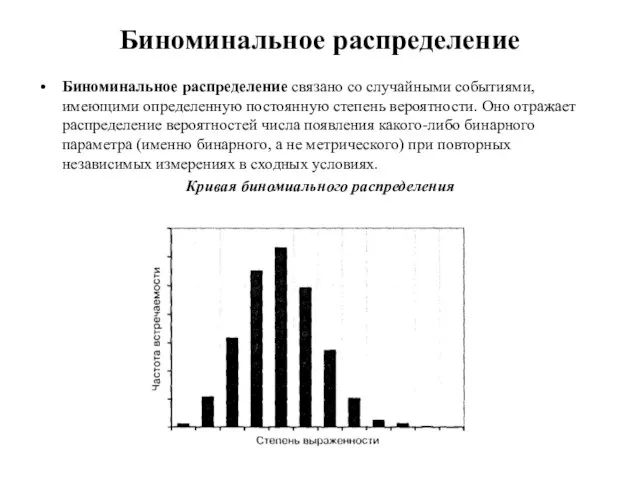
Биноминальное распределение
Биноминальное распределение связано со случайными событиями, имеющими определенную постоянную степень вероятности. Оно отражает распределение вероятностей числа появления какого-либо бинарного параметра (именно бинарного, а не метрического) при повторных независимых измерениях в сходных условиях.
Кривая биномиального распределения

Распределение Пуассона
Распределение Пуассона описывает случайные (редкие) события, вероятность появления которых в отдельных случаях мала, но число этих случаев достаточно велико.
Кривая распределения Стьюдента
Для выборок с числом наблюдений 30 или более, распределение Стьюдента равно нормальному распределению. При меньшем количестве наблюдений оно отличается от нормального, становится более плоским.
Кривая распределения Фишера
Распределение Фишера описывает значения F при случайном выборе из одной генеральной совокупности т групп по n объектов.
Связь с распределением Стьюдента обусловлена простым соотношением: t2 = F.

Тема 8. Статистическое оценивание и проверка гипотез
Статистические гипотезы.
Статистический вывод.
Ошибки 1 и 2 рода.
Степень свободы.
Статистический критерий

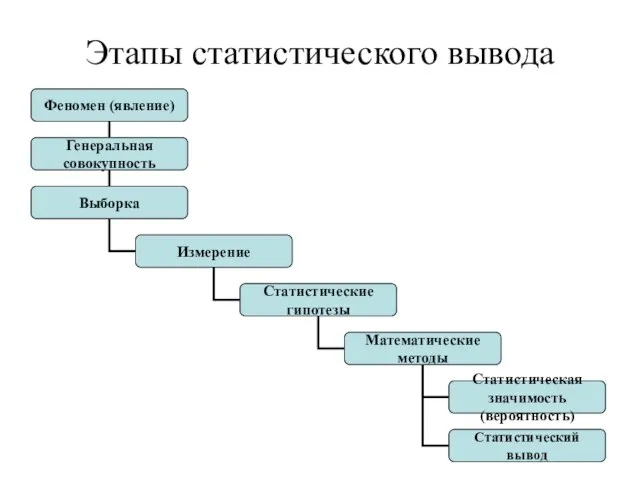
Этапы статистического вывода

Различают научные и статистические гипотезы.
Научные гипотезы (предположение) формулируются как предполагаемое решение проблемы.
Статистическая гипотеза – утверждение в отношении неизвестного параметра, сформулированное на языке математической статистики.
Любая научная гипотеза требует перевода на язык статистики.
Статистическая гипотеза необходима на этапе математической интерпретации данных эмпирических исследований. Большое количество статистических гипотез необходимо для подтверждения или опровержения основной – экспериментальной гипотезы.
Экспериментальная гипотеза – первична, статистическая – вторична.
Варианты гипотез:
1.О (различии) значении генеральных параметров;
2.О (взаимосвязи) отличии параметров от нуля;
3.О (нормальности распределения) законе распределения.

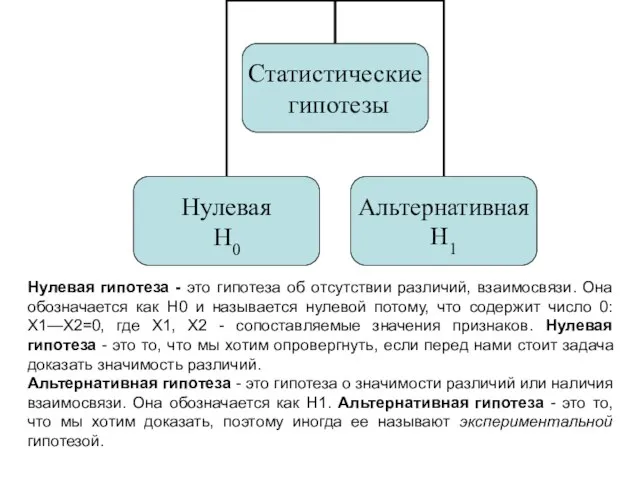
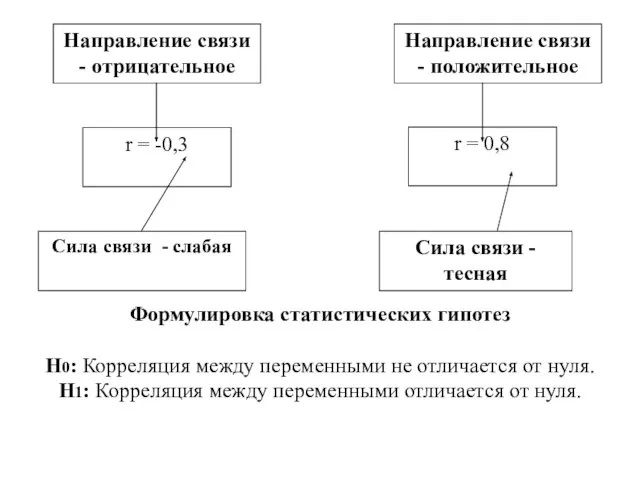
Нулевая гипотеза - это гипотеза об отсутствии различий, взаимосвязи. Она обозначается как H0 и называется нулевой потому, что содержит число 0: X1—Х2=0, где X1, X2 - сопоставляемые значения признаков. Нулевая гипотеза - это то, что мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий.
Альтернативная гипотеза - это гипотеза о значимости различий или наличия взаимосвязи. Она обозначается как Н1. Альтернативная гипотеза - это то, что мы хотим доказать, поэтому иногда ее называют экспериментальной гипотезой.

Алгоритм проверки статистических гипотез
Обоснование применения критерия.
Выполнение ограничений (если есть).
Формулирование статистических гипотез (Н0 и Н1).
Расчет критерия (таблица данных).
Определение уровня значимости (р).
Принятие одной из статистических гипотез.
Формулирование статистического вывода.
Интерпретация значимых результатов (р ≤ 0,05) + рисунок.
Н0 принимается при р > 0,05
Н1 принимается при р ≤ 0,05

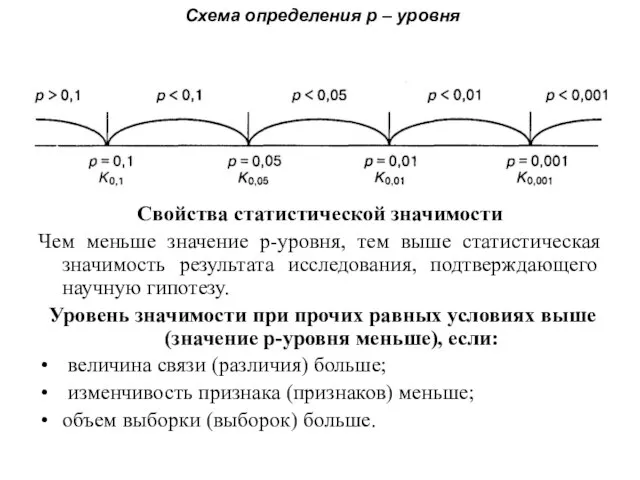
Статистическая значимость (Significant level, сокращенно Sig.), или р-уровень значимости (p-level).
Величину называют статисти́чески зна́чимой, если мала вероятность её случайного возникновения или еще более крайних величин, а так же это основной результат проверки статистической гипотезы.

Схема определения р – уровня
Свойства статистической значимости
Чем меньше значение р-уровня, тем выше статистическая значимость результата исследования, подтверждающего научную гипотезу.
Уровень значимости при прочих равных условиях выше (значение р-уровня меньше), если:
величина связи (различия) больше;
изменчивость признака (признаков) меньше;
объем выборки (выборок) больше.

Ошибки 1 и 2 рода
Ошибка I рода - ошибка, состоящая в том, что мы отклонили Н0, в то время как она верна.
Вероятность такой ошибки - α (или р), вероятность правильного решения: 1- α. Чем меньше α, тем больше вероятность правильного решения.
Ошибка II рода - ошибка, состоящая в том, что мы приняли Н0, в то время как она не верна.
Вероятность такой ошибки β. Вероятность (1 — β) называется мощностью (чувствительностью) критерия. Эта величина характеризует статистический критерий с точки зрения его способности отклонять Н0, когда она не верна.

Степень свободы
Число степеней свободы – это количество возможных направлений изменчивости признака.
Это характеристика распределения, используемая при проверке статистических гипотез, отражающая степень произвольности вариантов заполнения определенных групп, на которые квантифицируется распределение (обозначается как df или n-1).
Вариант заполнения интервалов оценок в выборке из 100 обследованных степень свободы равна трем (df = k-1= 4-1=3).

Показатели степеней свободы для зависимых и независимых выборок
Если имеются две независимые выборки, то число степеней свободы для первой из них составляет п1 – 1, а для второй п – 1. таким образом, число степеней свободы для этих независимых выборок будет составлять (п1 + п2) – 2.
В случае зависимых выборок число степеней свободы равно п – 1.
Показатель степени свободы наиболее широко используется при расчете статистических гипотез с использованием критериев Стьюдента, Фишера, z-критерия, критерия χ2. При применении каждого критерия и в каждом конкретном случае его использования существуют свои правила определения количества степеней свободы.

Статистический критерий
Статистический критерий – это решающее правило, обеспечивающее надежное поведение, т.е. принятие истинной и отклонение ложной гипотезы с высокой вероятностью.
Мощность критерия – это его способность выявлять различия, если они есть (т.е. это его способность не допустить ошибку).
Критерий включает в себя:
формулу расчета эмпирического значения критерия по выборочным статистикам;
правило (формулу) определения числа степеней свободы;
теоретическое распределение для данного числа степеней свободы;
правило соотнесения эмпирического значения критерия с теоретическим распределением для определения вероятности того, что Но верна.

Параметрические и непараметрические критерии
Параметрические критерии – это группа статистических критериев, которые включают в расчет параметры вероятностного распределения признака (средние и дисперсии).
Непараметрические критерии – это группа статистических критериев, которые не включают в расчёт параметры вероятностного распределения и основаны на оперировании частотами или рангами.
Преимущества и недостатки.
Параметрические критерии могут оказаться несколько более мощными, чем непараметрические, но только в том случае, если признак измерен по интервальной, абсолютной шкалах и нормально распределен. Кроме того, проверка распределения «на нормальность» требует достаточно сложных расчетов, результат которых заранее не известен.
Непараметрические критерии лишены всех этих ограничений и не требуют таких длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены лишь в одном – с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака.

Основание выбора критерия
а) простота;
б) более широкий диапазон использования (например, по отношению к данным, определенным по номинативной шкале, или по отношению к большим п);
в) применимость по отношению к неравным по объему выборкам;
г) большая информативность результатов.

Алгоритм работы с критериями
1. Обоснование применения критерия.
2. Выполнение ограничений критерия (если они есть).
3. Выдвижение статистических гипотез.
4. Расчет критерия.
5.Определение уровня значимости (р). (таблицы + графики)
6. Принятие/отвержение статистических гипотез
7. Формулирование статистического вывода.
8. Обсуждение полученных результатов (значимых) описание табличных и графических результатов.

Статистический вывод — это формулирование вывода на основе статистической значимости.
Результатом статистического вывода является статистическое суждение, например: о доверительном интервале, отвержении или принятии статистических гипотез.

Тема 9. Меры связи
Понятие корреляции.
Диаграмма рассеяния.
Классификация коэффициентов корреляции.
Корреляционные матрицы.
Интерпретация коэффициентов корреляции.
Графическое представление полученных взаимосвязей. Корреляционные плеяды.

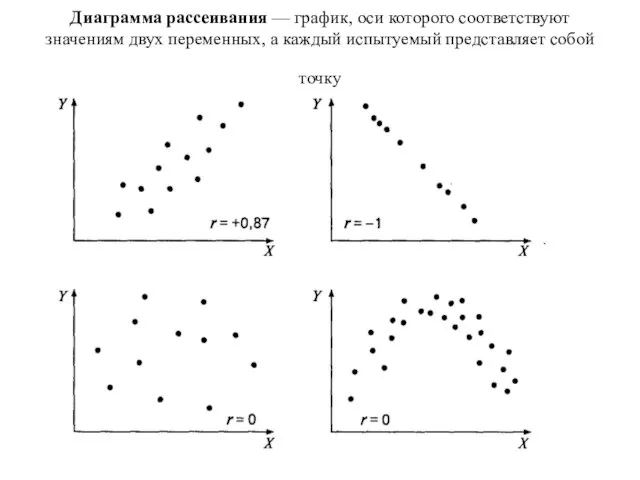
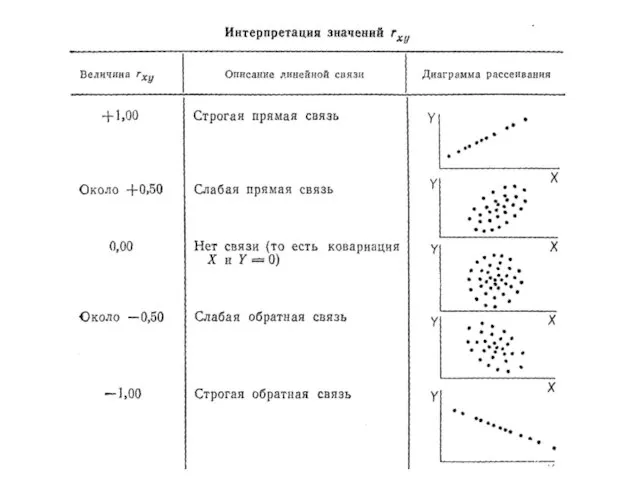
Понятие корреляции и ее основные параметры
Корреляционная связь – это согласованное изменение двух или более признаков.
Коэффициент корреляции — это количественная мера силы и направления вероятностной взаимосвязи двух переменных; принимает значения в диапазоне от -1 до +1.
Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот). Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции.
Направление связи определяется прямым или обратным соотношением зна­чений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь на­зывается прямой (положительной); если возрастанию значений одной пере­менной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной). Показателем направления связи является знак коэффициента корреляции.

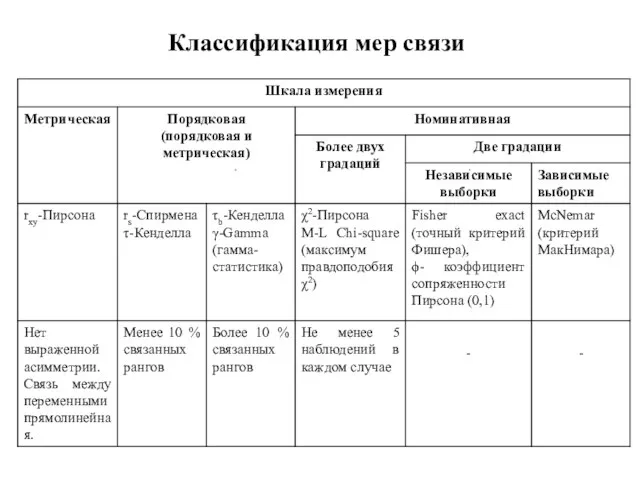
Классификация мер связи

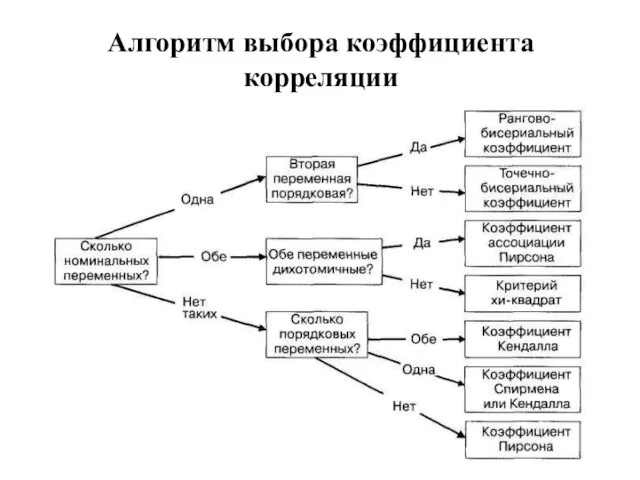
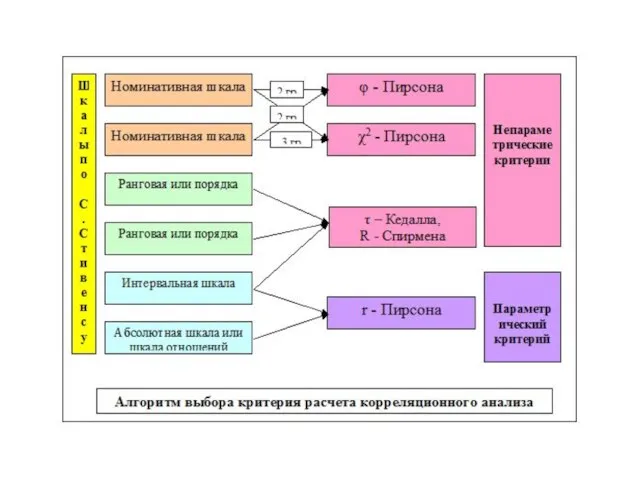
Алгоритм выбора коэффициента корреляции

Формулировка статистических гипотез
Н0: Корреляция между переменными не отличается от нуля.
Н1: Корреляция между переменными отличается от нуля.

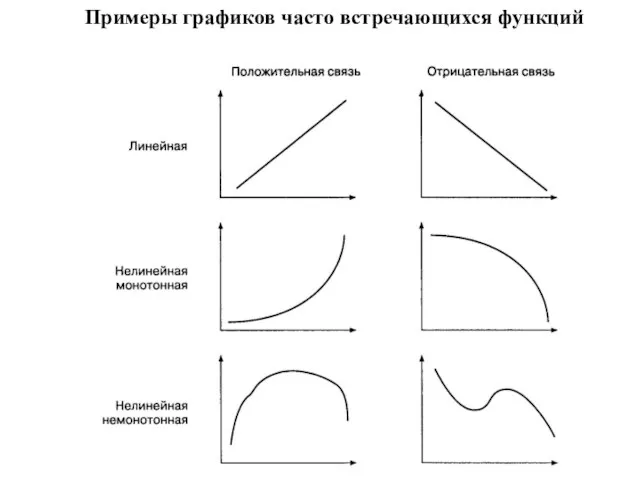
Виды связей
Взаимосвязи на языке математики обычно описываются при помощи функций, которые графически изображаются в виде линий.
Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная.
Если увеличение одной переменной связано с увеличением другой, то связь — положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь — отрицательная (обратная).
Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция — монотонная; в противном случае функцию называют немонотонной.

Примеры графиков часто встречающихся функций

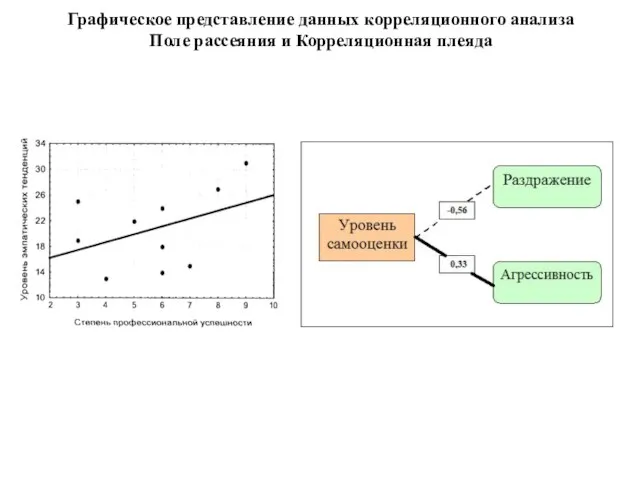
Диаграмма рассеивания — график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку

Классификация мер связи

Графическое представление данных корреляционного анализа
Поле рассеяния и Корреляционная плеяда

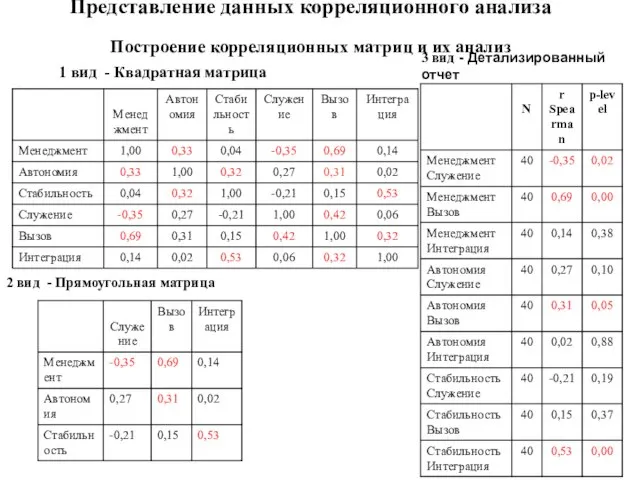
Представление данных корреляционного анализа
Построение корреляционных матриц и их анализ
1 вид - Квадратная матрица
2 вид - Прямоугольная матрица
3 вид - Детализированный отчет

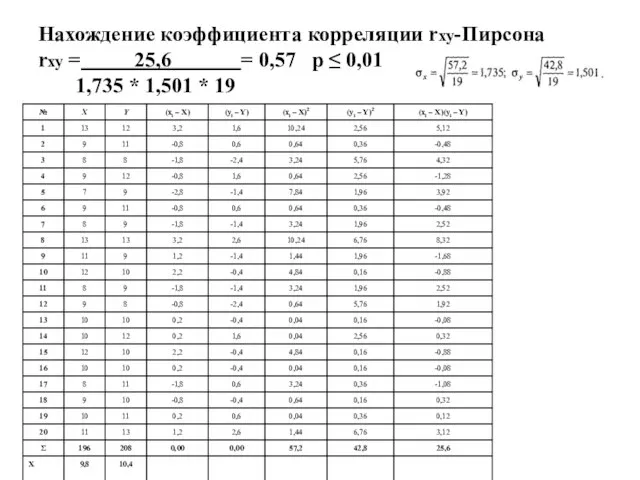
Коэффициент корреляции rxy- Пирсона
r-Пирсона (Pearson r) применяется для изучения взаимосвязи двух метрических переменных, измеренных на одной и той же выборке.
Ограничения
Обе переменные измерены в метрической шкале;
Обе переменные не имеют выраженной асимметрии;
Отсутствуют выбросы;
Связь между переменными прямолинейная.
Пояснения к формуле
(xi – Mx), (yi – My) – отклонения соответствующих значений переменных от своих средних величин;
N – количество испытуемых;
σх, σу – соответствующие стандартные отклонения.
Интерпретация коэффициента корреляции Пирсона
+1 – строгая прямая связь; -1 – строгая обратная связь
+0,5 – слабая прямая связь; -0,5 – слабая обратная связь
0,0 – нет связи

Нахождение коэффициента корреляции rxy-Пирсона
rxy = 25,6 = 0,57 р ≤ 0,01
1,735 * 1,501 * 19

Поле рассеяния

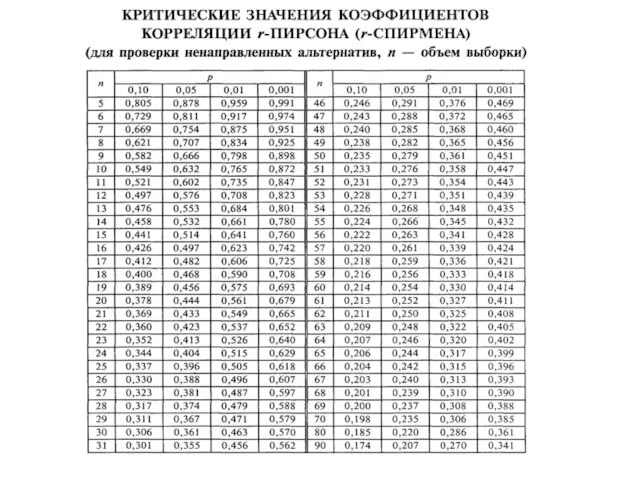
Коэффициенты ранговой корреляции rs-Спирмена и ι-Кендалла
Коэффициенты ранговой корреляции: r-Спирмена или ι-Кенделла применяются если обе переменные представлены в порядковой шкале, или одна из них — в порядковой, а другая — в метрической.
Ограничения
Обе переменные представлены в количественной шкале (метрической или ранговой);
Связь между переменными является монотонной (не меняет свой знак с изменением величины одной из переменных.
Отсутствие повторяющихся рангов (менее 10 % связанных рангов).
Формула rs-Спирмена и пояснения к формуле
d – разность между рангами по двум переменным для каждого испытуемого;
N – количество ранжируемых значений, в данном случае количество испытуемых
Интерпретация коэффициентов корреляции
+0,7 и выше – тесная положительная связь; -0,7 и выше – тесная отрицательная связь;
+0,4 и выше – умеренная положительная связь; -0,4 и выше – умеренная отрицательная связь;
+0,2 и – выше слабая положительная связь;-0,2 и – выше слабая отрицательная связь;
0,0 и выше – нет связи

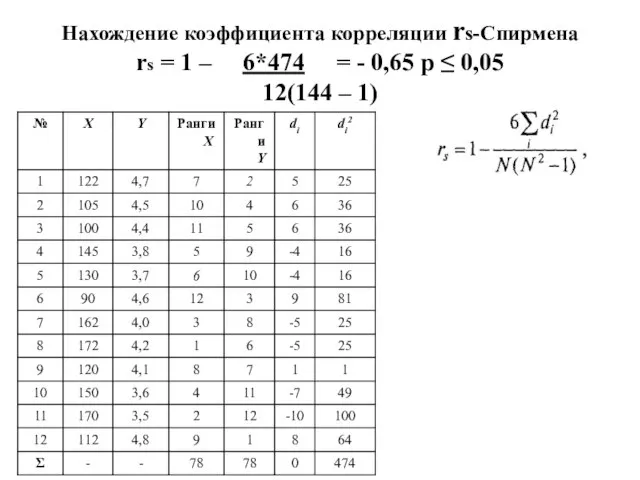
Нахождение коэффициента корреляции rs-Спирмена
rs = 1 – 6*474 = - 0,65 р ≤ 0,05
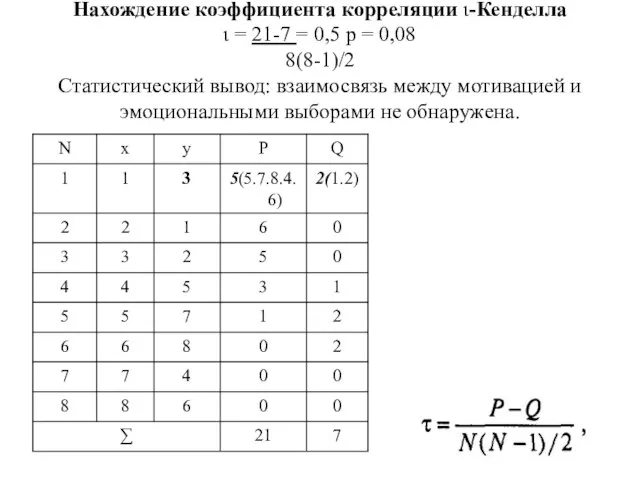
12(144 – 1)

Формула ι-Кенделла :
Пояснения к формуле
Р — общее число совпадений.
Q — общее число инверсий
N – количество испытуемых
Алгоритм
Данные упорядочиваются по переменной X.
Затем для каждого испытуемого подсчитывается, сколько раз его ранг по Y оказывается меньше, чем ранг испытуемых, находящихся ниже. Результат записывается в столбец «Совпадения». Сумма всех значений столбца «Совпадения» и есть Р — общее число совпадений, подставляется в формулу.
После чего, для каждого испытуемого подсчитывается сколько раз его ранг поYоказывается больше, чем ранг испытуемых, находящихся ниже. Сумма всех значений столбца «инверсии» и есть Q — общее число инверсий, которые подставляются в формулу

Нахождение коэффициента корреляции ι-Кенделла
ι = 21-7 = 0,5 р = 0,08 8(8-1)/2
Статистический вывод: взаимосвязь между мотивацией и эмоциональными выборами не обнаружена.

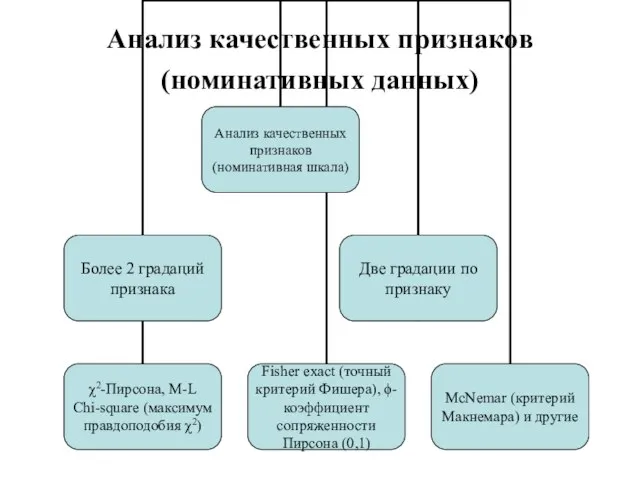
Тема 10. Анализ качественных признаков (номинативных данных)
Корреляция номинативных данных
критерий χ2-Пирсона
Корреляция бинарных данных
фи-коэффициент сопряженности Пирсона

Анализ качественных признаков (номинативных данных)

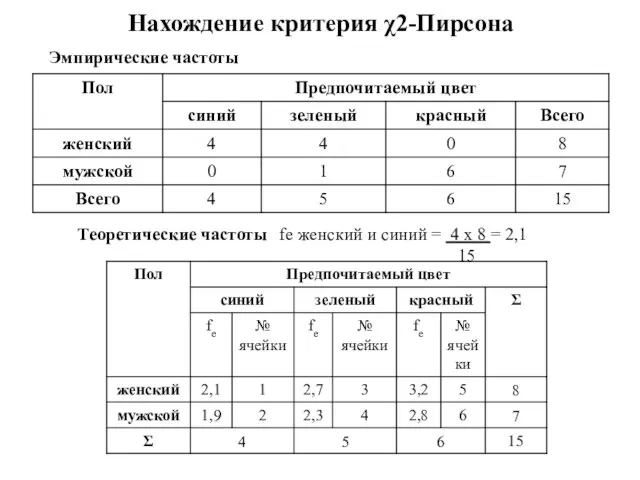
Корреляция номинативных данных
критерий χ2-Пирсона
Критерий χ2-Пирсона применяется если обе переменные представлены в номинативной шкале, одна из которых или обе имеют более двух градаций.
Ограничения
Ожидаемые частоты должны быть больше 5.
Суммы по строкам и по столбцам должны быть больше нуля.
Формула χ2-Пирсона и пояснения к формуле
fe = fj x fk df = (k – 1)x(j – 1)
n
fo – наблюдаемая частота (эмпирическая);
fe – ожидаемая частота (теоретическая);
n – общее количество наблюдений;
k – k – й столбец;
j – j-я строка.

Нахождение критерия χ2-Пирсона
Теоретические частоты fe женский и синий = 4 x 8 = 2,1
15
Эмпирические частоты

Нахождение критерия χ2-Пирсона
Расчет
χ2= 11,8
k = 3; j = 2; df = (k – 1)x(j – 1) = (3 – 1)х(2 – 1) = 2;
р ≤ 0,01
Статистический вывод: существует взаимосвязь между полом и
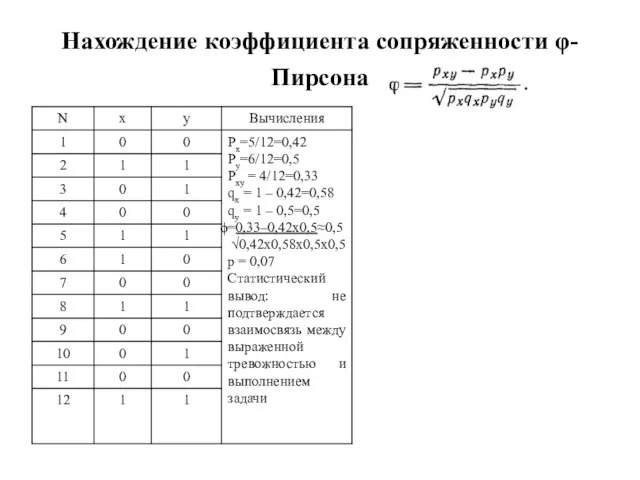
предпочтением цвета – мужчины значимо предпочитают красный цвет, а женщины синий и зеленый цвета с вероятностью ошибки менее 1 %.

Корреляция бинарных данных
фи-коэффициент сопряженности Пирсона
Коэффициент сопряженности φ-Пирсона применяется если обе переменные представлены в номинативной шкале, имеющей две градации.
Формула φ-Пирсона и пояснения к формуле
рх – доля имеющих 1 по х;
ру – доля имеющих 1 по y;
рху – доля тех, кто имеет 1 и по х и по у;
qx – доля имеющих 0 по х = 1 – рx
qy – доля имеющих 0 по у = 1 – рy

Нахождение коэффициента сопряженности φ-Пирсона

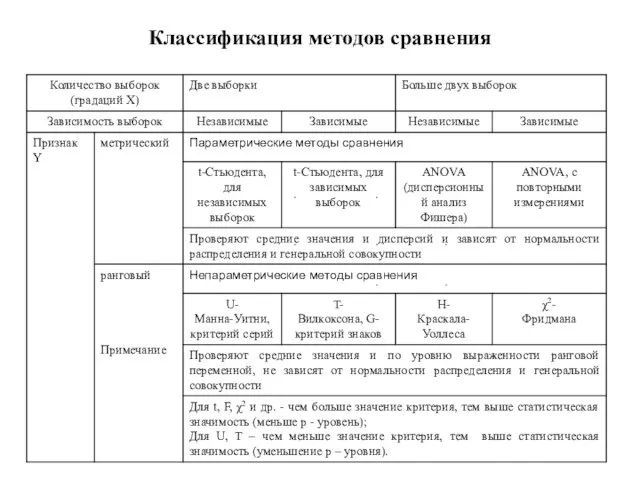
Тема 11. Анализ различий между 2 группами независимых выборок
Классификация методов сравнения
Представление данных сравнительного анализа
Параметрический критерий t-Стьюдента для двух независимых выборок
Непараметрический критерий U-Манна-Уитни для двух независимых выборок

Классификация методов сравнения

Методы сравнения
В зависимости от решаемых задач методы внутри этой группы классифицируются по трем основаниям:
Количество градаций X:
а) сравниваются 2 выборки;
б) сравниваются больше 2 выборок.
Зависимость выборок:
а) сравниваемые выборки независимы;
б)сравниваемые выборки зависимы.
Шкала У:
а) Y— ранговая переменная;
б) У— метрическая переменная.
По последнему основанию методы делятся на две большие группы: параметрические методы (критерии) — для метрических переменных и непараметрические методы (критерии) — для порядковых (ранговых) переменных. Параметрические методы проверяют гипотезы относительно параметров распределения (средних значений и дисперсий) и основаны на предположении о нормальном распределении в генеральной совокупности. Непараметрические методы не зависят от предположений о характере распределения и не касаются параметров этого распределения.
Независимые выборки характеризуются тем, что вероятность отбора любого испытуемого одной выборки не зависит от отбора любого из испытуемых другой выборки. Напротив, зависимые выборки характеризуются тем, что каждому испытуемому одной выборки поставлен в соответствие по определенному критерию испытуемый из другой выборки.В общем случае зависимые выборки предполагают попарный подбор испытуемых в сравниваемые выборки, а независимые выборки — независимый отбор испытуемых.
Формулировка статистических гипотез
Н0: Различий между выборками в уровне изучаемого признака не имеется.
Н1: Различия между выборками в уровне изучаемого признака имеются.

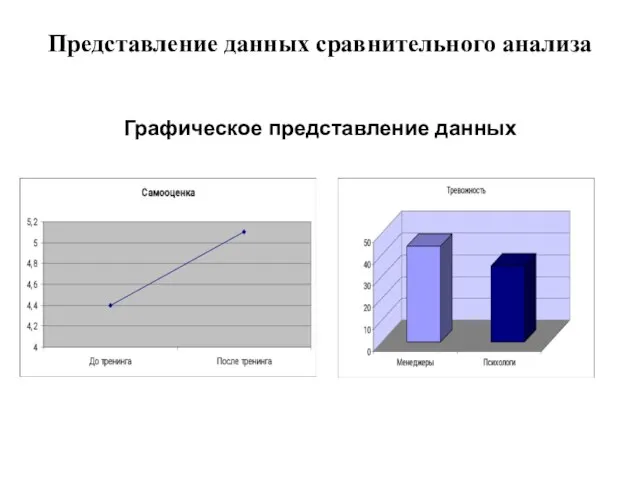
Представление данных сравнительного анализа
Графическое представление данных

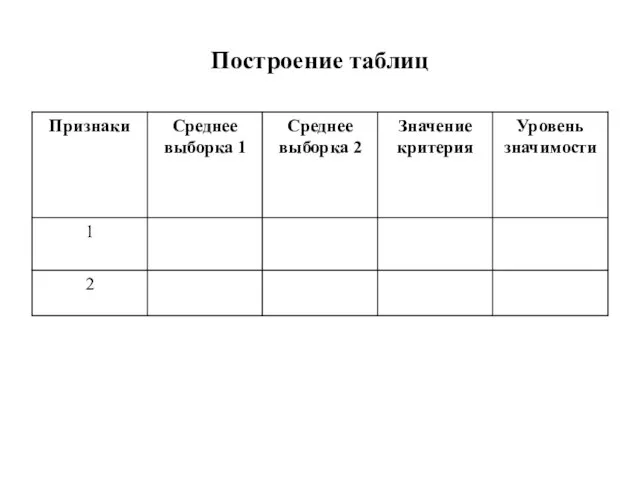
Построение таблиц

Параметрический критерий t-Стьюдента для двух независимых выборок
Метод позволяет проверить гипотезу о том, что средние значения двух генеральных совокупностей, из которых извлечены две сравниваемые независимые выборки, отличаются друг от друга.
Ограничения:
Распределения признака и в той, и в другой выборке существенно не отличаются от нормального.
Дисперсии выборок равны.
Признак измерен в метрической шкале.
Формула t-Стьюдента и пояснения к формуле
df = N1 + N2 – 2
М1 и М2 – средние значения в соответствующих выборках;
σ1 и σ2 – ст. отклонение в соответствующих выборках;
N1 и N2 – количество испытуемых в соответствующих выборках;
df - число степеней свободы.
Гипотезы:
Н0: признак в выборке 1 равен исследуемому признаку в выборке 2.
Н1: признак в выборке 1 не равен исследуемому признаку в выборке 2.

Параметрический критерий сравнения 2 групп (зависимых и независимых) t-Стьюдента
Данный критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

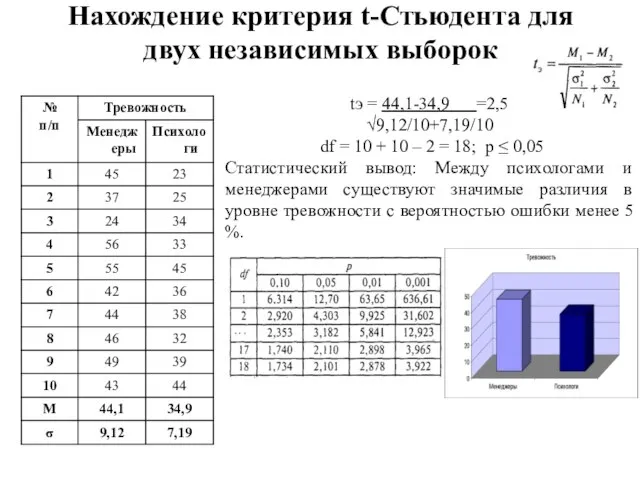
Нахождение критерия t-Стьюдента для двух независимых выборок
tэ = 44,1-34,9 =2,5
√9,12/10+7,19/10
df = 10 + 10 – 2 = 18; р ≤ 0,05
Статистический вывод: Между психологами и менеджерами существуют значимые различия в уровне тревожности с вероятностью ошибки менее 5 %.

Непараметрический критерий U-Манна-Уитни для двух независимых выборок
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он отражает степень совпадения (перекрещивания) двух рядов значений, то значение р-уровня тем меньше, чем меньше значение U.
Ограничения - нет.
Формула U-Манна-Уитни и пояснения к формуле
n — объем выборки Х;
m — объем выборки У,
Rx и Ry — суммы рангов для X и У в объединенном ряду.
В качестве эмпирического значения критерия берется наименьшее из Ux.и Uy. Чем больше различия, тем меньше эмпирическое значение U.
Гипотезы
H0: Уровень признака в группе 2 не ниже уровня признака в группе 1.
H1: Уровень признака в группе 2 ниже уровня признака в группе 1.

Нахождение критерия U-Манна-Уитни
Ш а г 1. Значения двух выборок объединяются в один ряд и упорядочиваются.
Ш а г 2. Обозначается принадлежность к выборке.
Ш а г 3. Значения ранжируются.
Ш а г 4 и 5. Выписываются ранги отдельно по Х отдельно по У.
Ш а г 6. Сумма рангов по Х и по У подставляется в формулу:
X(RX) и по Y(Ry): Rx = 46; Ry = 90.
Ux = 8 х 8 – 46 + 8(8+1)/2 = 18 + 72/2 = 18 + 36 = 54
Uy = 8 х 8 – 90 + 8(8+1)/2 = -26 + 72/2 = -26 + 36 = 10
Наименьшая сумма сравнивается с табличной и определяется р.
На уровне α = 0,05 принимается статистическая гипотеза о различии Х и Y по уровню выраженности признака. Уровень Y статистически достоверно выше уровня Х (р < 0,05).

Тема 12. Анализ различий между 2 группами зависимых выборок
Параметрический критерий t-Стьюдента для двух зависимых выборок
Непараметрический критерий Т-Уилкоксона для сравнения двух зависимых групп

Параметрический критерий t-Стьюдента для двух зависимых выборок
Метод позволяет проверить гипотезу о том, что средние значения двух генеральных совокупностей, из которых извлечены две сравниваемые зависимые выборки, отличаются друг от друга. Допущение зависимости чаще всего значит, что признак измерен на одной и той же выборке дважды, например, до воздействия и после него.
Ограничения:
Распределения признака и в той, и в другой выборке существенно не отличаются от нормального.
Дисперсии выборок равны.
Признак измерен в метрической шкале.
Формула t-Стьюдента и пояснения к формуле
Md – средняя разность значений;
σd – стандартное отклонение разностей;
N – количество испытуемых в выборке
df - число степеней свободы.
Гипотезы
Н0: Между показателями, полученными (измеренными) в разных условиях, существуют лишь случайные различия.
H1: Между показателями, полученными в разных условиях, существуют неслучайные различия.

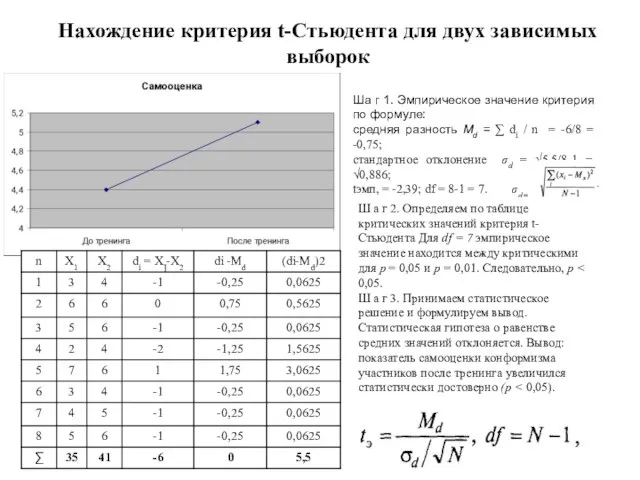
Нахождение критерия t-Стьюдента для двух зависимых выборок
Ша г 1. Эмпирическое значение критерия по формуле:
средняя разность Md = ∑ di / n = -6/8 = -0,75;
стандартное отклонение σd = √5.5/8-1 = √0,886;
tэмп, = -2,39; df = 8-1 = 7. σd=
Ш а г 2. Определяем по таблице критических значений критерия t-Стьюдента Для df = 7 эмпирическое значение находится между критическими для р = 0,05 и р = 0,01. Следовательно, р < 0,05.
Ш а г 3. Принимаем статистическое решение и формулируем вывод. Статистическая гипотеза о равенстве средних значений отклоняется. Вывод: показатель самооценки конформизма участников после тренинга увеличился статистически достоверно (р < 0,05).

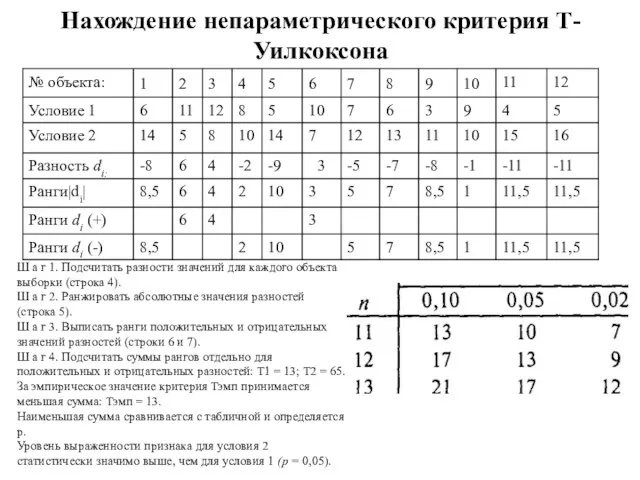
Непараметрический критерий Т-Уилкоксона для сравнения двух зависимых групп
Критерий предназначен для оценки различий между двумя зависимыми выборками по уровню какого-либо признака, количественно измеренного. Он отражает степень совпадения (перекрещивания) двух рядов значений.
Ограничения - нет.
Формула Т-Уилкоксона и пояснения к формуле
Подсчитываются суммы рангов для положительных и отрицательных разностей. Затем меньшая из сумм принимается в качестве эмпирического значения критерия, значение которого сравнивается с табличным значением для данного объема выборки. Чем больше различия, тем меньше эмпирическое значение Т, тем меньше значение р-уровня.
Гипотезы
Н0: Между показателями, полученными (измеренными) в разных условиях, существуют лишь случайные различия.
H1: Между показателями, полученными в разных условиях, существуют неслучайные различия.

Нахождение непараметрического критерия Т-Уилкоксона
Ш а г 1. Подсчитать разности значений для каждого объекта выборки (строка 4).
Ш а г 2. Ранжировать абсолютные значения разностей (строка 5).
Ш а г 3. Выписать ранги положительных и отрицательных значений разностей (строки 6 и 7).
Ш а г 4. Подсчитать суммы рангов отдельно для положительных и отрицательных разностей: T1 = 13; Т2 = 65. За эмпирическое значение критерия Тэмп принимается меньшая сумма: Тэмп = 13.
Наименьшая сумма сравнивается с табличной и определяется р.
Уровень выраженности признака для условия 2 статистически значимо выше, чем для условия 1 (р = 0,05).

Тема 13. Анализ различий между 3 и более группами независимых выборок
Непараметрический критерий Н-Краскала-Уоллеса для сравнения 3 и более групп
Критерий χ2-Фридмана для сравнения 3-х и более зависимых выборок

Непараметрический критерий Н-Краскала-Уоллеса для сравнения 3 и более групп
Критерий Н-Краскала-Уоллеса позволяет проверять гипотезы о различии более двух выборок по уровню выраженности изучаемого признака. Он оценивает степень пересечения (совпадения) нескольких рядов значений измеренного признака. Чем меньше совпадений, тем больше различаются ряды, соответствующие сравниваемым выборкам.
Ограничения - нет.
Формула Н-Краскала-Уоллеса и пояснения к формуле
N — суммарная численность всех выборок;
k — количество сравниваемых выборок;
Ri — сумма рангов для выборки i;
ni, — численность выборки i.
Чем сильнее различаются выборки, тем больше вычисленное значение Н и тем меньше p-уровень значимости.
При отклонении Н0 для утверждений о том, что уровень выраженности признака в какой-то из сравниваемых выборок выше или ниже, необходимо парное соотнесение выборок по критерию U-Манна-Уитни.
Гипотезы
H0: Между выборками 1, 2, 3 и т. д. существуют лишь случайные различия по уровню исследуемого признака.
H1: Между выборками 1, 2, 3 и т. д. существуют неслучайные различия по уровню исследуемого признака.

Нахождение Н-Краскала-Уоллеса
Шаг 1. Значения объединяются в один упорядоченный ряд. Обозначается принадлежность каждого значения к выборке (строки 1 и 2).
Ш а г 2. Значения выборок ранжируются и выписываются отдельно ранги для каждой выборки (строки 3-6).
Ш а г 3. Вычисляются суммы рангов для каждой выборки Rx = 46; R2 = 49; R3 = 41.
Ш а г 4. Н = 12/ 16(16 + 1) х (462/8 + 492/5 + 412/3) – 3(16 + 1) = 7,725
Шаг 5. Определяется р-уровень значимости. Хотя сравниваются 3 выборки, но объем одной из них больше 5, поэтому вычисленное Н сравнивается с табличным значением χ2 (приложение 4) для числа степеней свободы df = 3—1=2. Эмпирическое значение Н находится между критическими для р = 0,05 и р = 0,01. Следова­тельно, р < 0,05.
Ш а г 6. На уровне р = 0,05 гипотеза Но отклоняется. Содержательный вывод: сравниваемые выборки различаются статистически достоверно по уровню выраженности признака (р < 0,05).

Критерий χ2-Фридмана для сравнение 3-х и более зависимых выборок
Критерий χ2-Фридмана позволяет проверять гипотезы о различии более двух зависимых выборок (повторных измерений) по уровню выраженности изучаемого признака. Чем больше различаются зависимые выборки по изучаемому признаку, тем больше эмпирическое значение χ2-Фридмана.
Ограничения - нет.
Формула χ2-Фридмана и пояснения к формуле
N — число объектов (испытуемых),
k — количество условий (повторных измерений),
Ri — сумма рангов для условия i.
При расчетах для определения p-уровня пользуются таблицами критических значений. Если k=3, N > 9 или k > 3, N > 4, то пользуются обычной таблицей для χ2, df = к — 1. Если к = 3, N < 10 или k = 4, N < 5, то пользуются дополнительными таблицами критических значений χ2- Фридмана.
Для утверждений о том, что уровень выраженности признака в какой-то из сравниваемых выборок выше или ниже, необходимо парное соотнесение выборок по критерию Т-Вилкоксона.
Гипотезы
Н0: Между показателями, полученными (измеренными) в разных условиях, существуют лишь случайные различия.
H1: Между показателями, полученными в разных условиях, существуют неслучайные различия.

Нахождение критерия χ2-Фридмана
Шаг 1. Для каждого объекта условия ранжируются (по строке).
Ш а г 2. Вычисляется сумма рангов для каждого условия: R1 = 14, R2 = 15, R3 = 9, R4=22.
Ш а г 3. Вычисляется значение χ2-Фридмана по формуле :
χ2 = [ 12/ 6 x 4(4 + 1) x (142+152+92+222)] –3 x 6(4 + 1) = 8,6;
df =3
Ш а г 4. Определяется р-уровень значимости. Так как к > 3, N > 4, то пользуются обычной таблицей для χ2 (приложение 4). Эмпирическое значение χ2 находится меж­ду критическими для р = 0,05 и р = 0,01. Следовательно, р< 0,05.
Ш а г 5. Принимается статистическое решение и формулируется содержательный вывод. На уровне а = 0,05 гипотеза Но отклоняется. Содержательный вывод: срав­ниваемые условия статистически достоверно различаются по уровню выраженности признака (р < 0,05).

Тема 14. Дисперсионный анализ (ANOVA)
Однофакторный дисперсионный анализ ANOVA
Методы множественного сравнения

Дисперсионный анализ ANOVA
(от англоязычного ANalysis Of VАriance)
Анализ предназначен для изучения различий у трех и более выборок в уровне выраженности признака. Типичная схема эксперимента сводится к изучению влияния независимой переменной (одной или нескольких) на зависимую переменную.
Выделяются два вида переменных – независимая и зависимая. Независимая переменная (Independent Variable) представляет собой качественно определенный (номинативный) признак, имеющий две или более градации. Каждой градации независимой переменной соответствует выборка объектов (испытуемых), для которых определены значения зависимой переменной. Зависимая переменная (Dependent Variable) (должна быть представлена в метрической шкале) в экспериментальном исследовании рассматривается как изменяющаяся под влиянием независимых переменных.
Ограничения
дисперсии выборок, соответствующих разным градациям фактора, равны между собой
Статистические гипотезы
Н0: средние значения признака в выборках 1, 2, 3, … соответствующих разным уровням фактора не отличаются.
Н1: средние значения признака в выборках 1, 2, 3, … соответствующих разным уровням фактора отличаются.

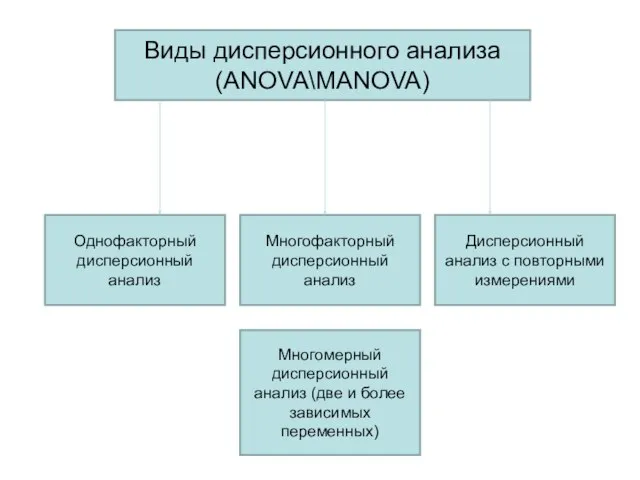
Виды дисперсионного анализа (ANOVA\MANOVA)
Однофакторный дисперсионный анализ
Многофакторный дисперсионный анализ
Дисперсионный анализ с повторными измерениями
Многомерный дисперсионный анализ (две и более зависимых переменных)

Метод однофакторного дисперсионного анализа применяется в тех случаях, когда исследуются изменения результативного признака под влиянием изменяющихся условий или градаций какого-либо фактора. Градаций фактора должно быть не менее трех, т.е. когда в распоряжении есть три или более независимые выборки, полученные из одной генеральной совокупности путем изменения какого-либо независимого фактора.
Для этих выборок предполагают, что они имеют разные выборочные средние и одинаковые выборочные дисперсии. Поэтому необходимо ответить на вопрос, оказал ли этот фактор существенное влияние на разброс выборочных средних или разброс является следствием случайностей, вызванных небольшими объемами выборок. Другими словами если выборки принадлежат одной и той же генеральной совокупности, то разброс данных между выборками (между группами) должен быть не больше, чем разброс данных внутри этих выборок (внутри групп).
Однофакторный дисперсионный анализ

Последовательность вычислений для ANOVA
В общей изменчивости зависимой переменной выделяются основные ее составляющие. (В однофакторном ANOVA их две: внутригрупповая (случайная) и межгрупповая (факторная) изменчивость.) После этого вычисляются соответствующие показатели в следующей последовательности:
□ суммы квадратов (SS) – общая, внутригрупповая и межгрупповая;
□ числа степеней свободы (df): dftotal=N-1; dfbg = k-1(k – группа); dfwg = df total –dfbg;
□ средние квадраты (MS);
□ F-отношения;
□ р-уровни значимости.
После отклонения Н0 применяется парное сравнение групп по критерию Шеффе.

Формулы расчетов однофакторного дисперсионного анализа

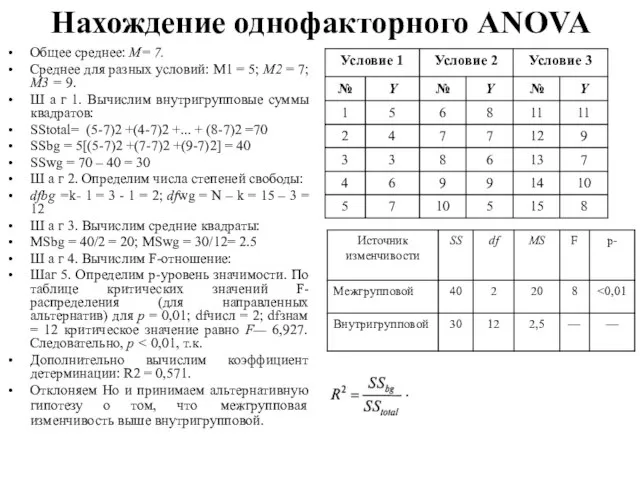
Нахождение однофакторного ANOVA
Общее среднее: М= 7.
Среднее для разных условий: М1 = 5; М2 = 7; М3 = 9.
Ш а г 1. Вычислим внутригрупповые суммы квадратов:
SStotal= (5-7)2 +(4-7)2 +... + (8-7)2 =70
SSbg = 5[(5-7)2 +(7-7)2 +(9-7)2] = 40
SSwg = 70 – 40 = 30
Ш а г 2. Определим числа степеней свободы:
dfbg =k- 1 = 3 - 1 = 2; dfwg = N – k = 15 – 3 = 12
Ш а г 3. Вычислим средние квадраты:
MSbg = 40/2 = 20; MSwg = 30/12= 2.5
Ш а г 4. Вычислим F-отношение:
Шаг 5. Определим p-уровень значимости. По таблице критических значений F-распределения (для направленных альтернатив) для р = 0,01; dfчисл = 2; dfзнам = 12 критическое значение равно F— 6,927. Следовательно, р < 0,01, т.к.
Дополнительно вычислим коэффициент детерминации: R2 = 0,571.
Отклоняем Но и принимаем альтернативную гипотезу о том, что межгрупповая изменчивость выше внутригрупповой.

Многофакторный дисперсионный анализ
Многофакторный дисперсионный анализ предназначен для изучения влияния двух и более независимых переменных, с двумя и боле градациями на зависимую переменную. Данный вид анализа подразумевает факторный план, в котором проверяются одновременно несколько гипотез:
1. Гипотезы о раздельном влиянии каждой из независимых переменных.
2. Гипотезы о взаимодействии переменных, а именно – как присутствие одной из независимых переменных влияет на эффект воздействия другой .
Как указывает В.Н. Дружинин, факторное планирование заключается в том, чтобы все уровни независимых переменных сочетались друг с другом. При этом количество групп равно числу сочетаний градаций (уровней) всех независимых переменных.

Дисперсионный анализ с повторными измерениями
Анализ позволяет проверить гипотезы о различии более двух зависимых выборок (повторных измерений) по уровню выраженности изучаемого признака. При этом допускается наличие межгрупповых факторов, а также несколько внутригрупповых. Для этого используется критерий F-Фишера, который тем больше, чем больше различаются зависимые выборки по изучаемому признаку.
Специфика ANOVA с повторными измерениями состоит в том, что из остаточной изменчивости (внутригрупповой) вычитается компонент, обусловленный индивидуальными различиями. Тем самым уменьшается дисперсия ошибки факторной модели и повышается чувствительность метода к воздействию факторов на зависимую переменную.

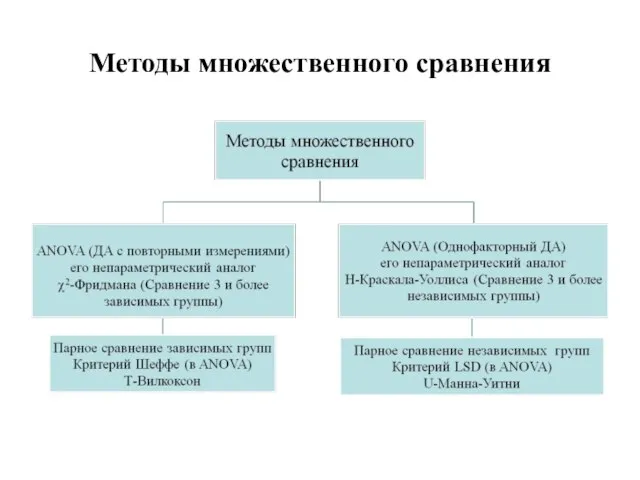
Методы множественного сравнения

Тема 15. Многомерные методы
Определение и классификация многомерных методов
Регрессионный анализ (частный случай множественного регрессионного анализа)
Множественный регрессионный анализ
Дискриминантный анализ
Факторный анализ
Кластерный анализ
Многомерное шкалирование

Многомерные методы - это математические модели в отношении многостороннего (многомерного) описания изучаемых явлений. ММ воспроизводят мыслительные операции человека, но в отношении таких данных, непосредственное осмысление которых невозможно в силу нашей природной ограниченности. Многомерные методы выполняют такие интеллектуальные функции, как структурирование эмпирической информации (факторный анализ), классификация (кластерный анализ), экстраполяция (множественный регрессионный анализ), распознавание образов (дискриминантный анализ) и т. д.
Моделирование – это претендующее на адекватность построение и описание образа или символа действительности, некоторого аспекта реальности. Суть ее в том, что проект исследования может быть моделью.

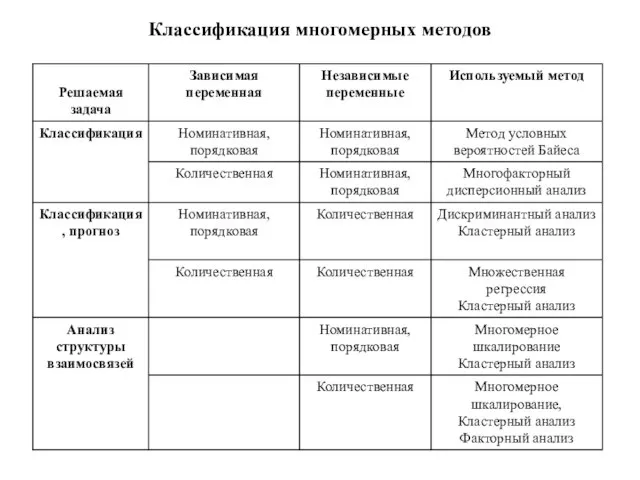
Классификация многомерных методов

Регрессионный анализ (частный случай множественного регрессионного анализа)
Регрессионный анализ — основан на коэффициенте детерминации. Регрессионный анализ применяется, для предсказания значения одной переменной, если известны значения другой, т.е. для исследования взаимосвязи зависимой одной у и одной независимой х переменных.
Линия регрессии, обобщает все точки рассеяния наилучшим способом из возможных. Иными словами, абсолютные значения расстояний по вертикали между каждой точкой графика и линией регрессии минимальны.
Переменная, по которой предсказывают, называется предикторной. Обычно ее значения откладываются по оси X.
Переменная, которую предсказывают, называется критериальной. Ее значения откладываются по оси Y.

Уравнение линейной регрессии
Если переменные пропорциональны друг другу, то графически связь между ними можно представить в виде прямой линии с положительным (прямая пропорция) или отрицательным (обратная пропорция) наклоном. Кроме того, если известна пропорция между переменными, заданная уравнением графика прямой линии, то по известным значениям переменной Х можно точно предсказать значения переменной Y.
На практике связь между двумя переменными, если она есть, является вероятностной и графически выглядит как облако рассеивания эллипсоидной формы. Этот эллипсоид, однако, можно представить (аппроксимировать) в виде прямой линии, или линии регрессии.
Линия регрессии (Regression Line) — это прямая, построенная методом наименьших квадратов: сумма квадратов расстояний (вычисленных по оси Y) от каждой точки графика рассеивания до прямой является минимальной:
где уi, — истинное i-значение У,
уi, — оценка i-значения Упри помощи линии (уравнения) регрессии,
еi,-= уi-yi,— ошибка оценки.
Уравнение регрессии имеет вид:
где b — коэффициент регрессии (Regression Coefficient), задающий угол наклона прямой;
а — свободный член, определяющий точку пересечения прямой оси Y.
Угловой коэффициент регрессии (b) показывает, насколько в среднем величина признака у изменяется при соответствующем изменении на единицу признака х. Таким образом, если на некоторой выборке измерены две переменные, которые коррелируют друг с другом, то, вычислив коэффициенты регрессии, мы получаем принципиальную возможность предсказания неизвестных значений одной переменной (Y- зависимая переменная) по известным значениям другой переменной (Х – независимая переменная).

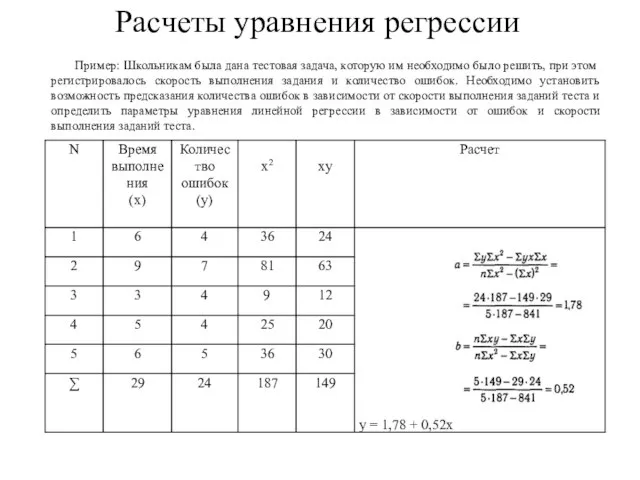
Расчеты уравнения регрессии
Пример: Школьникам была дана тестовая задача, которую им необходимо было решить, при этом регистрировалось скорость выполнения задания и количество ошибок. Необходимо установить возможность предсказания количества ошибок в зависимости от скорости выполнения заданий теста и определить параметры уравнения линейной регрессии в зависимости от ошибок и скорости выполнения заданий теста.

Множественный регрессионный анализ
Множественный регрессионный анализ (МРА) предназначен для изучения взаимосвязи одной переменной (зависимой, результирующей - у) и нескольких других переменных (независимых, исходных - х). Частный случай регрессионный анализ для исследования взаимосвязи зависимой одной у и одной независимой х переменных.
Ограничения
1. Главное требование к исходным данным — отсутствие линейных взаимосвязей между переменными, когда одна переменная является линейной производной другой переменной. Следует избегать включения в анализ переменных, корреляция между которыми близка к 1, так как сильно коррелирующая переменная не несет для анализа новой информации, добавляя излишний «шум».
2. Следующее требование — переменные должны быть измерены в метрической шкале (интервалов или отношений) и иметь нормальное распределение.

Основными целями МРА являются
Определение того, в какой мере «зависимая» переменная связана с совокупностью «независимых» переменных, какова статистическая значимость этой взаимосвязи. Показатель — коэффициент множественной корреляции (КМК - R) и его статистическая значимость по критерию F-Фишера,
Определение существенности вклада каждой «независимой» переменной в оценку «зависимой» переменной, отсев несущественных для предсказания «независимых» переменных. Показатели — регрессионные коэффициенты β, их статистическая значимость по критерию t-Стьюдента.
Анализ точности предсказания и вероятных ошибок оценки «зависимой» переменной. Показатель — квадрат КМК (КМД - R2), интерпретируемый как доля дисперсии «зависимой» переменной, объясняемая совокупностью «независимых» переменных. Вероятные ошибки предсказания анализируются по расхождению (разности) действительных значений «зависимой» переменной и оцененных при помощи модели МРА.
Оценка (предсказание) неизвестных значений «зависимой» переменной по известным значениям «независимых» переменных. Осуществляется по вычисленным параметрам множественной регрессии.

Дискриминантный анализ
Предназначен для изучения взаимосвязи одной переменной (зависимой, результирующей - у) и нескольких других переменных (независимых, исходных - х).
Ограничения
Зависимая переменная должна быть представлена в номинативной шкале, а независимые измерены в метрической шкале (интервалов или отношений) и иметь нормальное распределение.
Дискриминантный анализ позволяет решить две группы проблем:
Интерпретировать различия между классами, то есть ответить на вопросы: насколько хорошо можно отличить один класс от другого, используя данный набор переменных; какие из этих переменных наиболее существенны для различения классов.
Классифицировать объекты, то есть отнести каждый объект к одному из классов, исходя только из значений дискриминантных переменных.

Основные результаты дискриминантного анализа
Определение статистической значимости различения классов при помощи данного набора дискриминантных переменных. Показатели — λ-Вилкса, χ2-тест, р-уровень значимости.
2. Выяснение вклада каждой переменной в дискриминантный анализ. Определяется по значениям критерия F-Фишера, толерантности и статистики F-удаления.
3. Вычисление расстояний между центроидами классов и определение их статистической значимости по F-критерию.
4. Анализ канонических функций, их интерпретация через дискриминантные переменные (по стандартизированным и структурным коэффициентам канонических функций).
5. Классификация «известных» и «неизвестных» объектов при помощи расстояний или значений априорных вероятностей. Качество классификации определяется совпадением действительной классификации и пред­сказанной для «известных» объектов. Мерой качества может служить ве­роятность ошибочной классификации как соотношение количества оши­бочного отнесения к общему количеству «известных» объектов.
6. Графическое представление всех объектов и центроидов классов в осях канонических функций.

Факторный анализ
Главная цель факторного анализа — уменьшение размерности исходных данных.
Результатом факторного анализа является переход от множества исходных переменных к существенно меньшему числу новых переменных — факторов. Фактор при этом интерпретируется как причина совместной изменчивости нескольких исходных переменных.
Основное назначение факторного анализа — анализ корреляций множества признаков.
Область применения факторного анализа (задачи)
1. Исследование структуры взаимосвязей переменных. В этом случае каждая группировка переменных будет определяться фактором, по которому эти переменные имеют максимальные нагрузки. Нагрузки исследуемых факторов представляют корреляцию с общими факторами.
2. Идентификация факторов как скрытых (латентных) переменных — причин взаимосвязи исходных переменных.
3. Вычисление значений факторов для испытуемых как новых, интегральных переменных. При этом число факторов существенно меньше числа исходных переменных. В этом смысле факторный анализ решает задачу сокращения количества признаков с минимальными потерями исходной информации.

Основные этапы факторного анализа
Выбор исходных данных.
Предварительное решение проблемы числа факторов: используются критерий отсеивания Р. Кетелла (требует построения графика) и критерий Г. Кайзера (определяется по числу компонент, собственные значения которых больше 1).
Факторизация матрицы интеркорреляций, вращение факторов (Задается число факторов, производится вращение методом «Варимакс-нормализованное». Результатом данного этапа является матрица факторных нагрузок (факторная структура) .
Интерпретация факторов: По каждому фактору выписывают наименования (обозначения) переменных, имеющих наибольшие нагрузки по этому фактору — выделенных на предыдущем шаге. При этом обязательно учитывается знак факторной нагрузки переменной. Если знак отрицательный, это отмечается как противоположный полюс переменной. После такого просмотра всех факторов каждому из них присваивается наименование, обобщающее по смыслу включенные в него переменные.

Кластерный анализ
Кластерный анализ — это процедура упорядочивания объектов в сравнительно однородные классы на основе попарного сравнения этих объектов по предварительно определенным и измеренным критериям.
Кластерный анализ решает задачу построения классификации, то есть разделения исходного множества объектов на группы (классы, кластеры).
Классификация объектов — это группирование их в классы так, чтобы объекты в каждом классе были более похожи друг на друга, чем на объекты из других классов.
Задачи кластерного анализа:
разбиение совокупности испытуемых на группы по измеренным признакам с целью дальнейшей проверки причин межгрупповых различий по внешним критериям, например, проверка гипотез о том, проявляются ли типологические различия между испытуемыми по измеренным признакам;
применение кластерного анализа как значительно более простого и наглядного аналога факторного анализа, когда ставится только задача группировки признаков на основе их корреляции.

Этапы кластерного анализа
1. Отбор объектов для кластеризации. Объектами могут быть, в зависимости от цели исследования: а) испытуемые; б) объекты, которые оцениваются испытуемыми; в) признаки, измеренные на выборке испытуемых.
Определение множества переменных, по которым будут различаться объекты кластеризации. Для испытуемых — это набор измеренных признаков, для оцениваемых объектов — субъекты оценки, для признаков — испытуемые.
Определение меры различия между объектами кластеризации. Это первая проблема, которая является специфичной для методов анализа различий: многомерного шкалирования и кластерного анализа.
Выбор и применение метода классификации для создания групп сходных объектов. Это вторая и центральная проблема кластерного анализа. Ее весомость связана с тем, что разные методы кластеризации порождают разные группировки для одних и тех же данных. Наиболее популярные методы: одиночной связи, полной связи и средней связи.
Проверка достоверности разбиения на классы (используются критерии сравнения).

Многомерное шкалирование
Основная цель многомерного шкалирования (МШ) — выявление структуры исследуемого множества объектов
Главная задача МШ — реконструкция психологического пространства, заданного небольшим числом измерений-шкал, которые интерпретируются как критерии, лежащие в основе различий стимулов.

Основные этапы многомерного шкалирования
Определение величины стресса (φ-Stress), который является показателем точности - наиболее приемлемый для него диапазон от 0,05 до 0,2. Вычисление коэффициентов отчуждения (D-star) и напряжения (D-hat). Чем меньше эти величины тем лучше воспроизведена матрица расстояния в наблюдаемой модели.
Построение итоговой конфигурации нагрузки объектов по выделенным шкалам.
Построение графика.
Интерпретация шкал по итоговой конфигурации и графику (интерпретация шкал осуществляется через входящие в них объекты).

Тема 16. Математическое моделирование в психологии
Системные подходы.
Теория функциональных систем.
Становление кибернетики.
Системный анализ.
Теория катастроф.
Методы математического моделирования в психодиагностике: априорные и апостериорные модели.
Проблема искусственного интеллекта.

Моделирование
Моделирование — это претендующее на адекватность построение и описание образа или символа действительности, некоторого аспекта реальности. Суть ее в том, что проект исследования может быть моделью.
В основу моделирования сложных систем и явлений положена теория подобия, которая базируется на трех теоремах подобия.
Первая гласит, что у явлений, подобных в том или ином смысле (физически, математически и т. д.), можно найти определенные сочетания параметров, называемые критериями подобия, которые имеют одинаковые (численно или по функциональным проявлениям) значения.
Вторая теорема определяет, что всякое полное уравнение физического или другого процесса, записанное в определенной системе единиц, может быть представлено в виде зависимости между безразмерными соотношениями из входящих в уравнение параметров, которые и являются критериями подобия.
Третья теорема подобия заключается в том, что необходимыми и достаточными условиями подобия являются пропорциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия изучаемого явления.

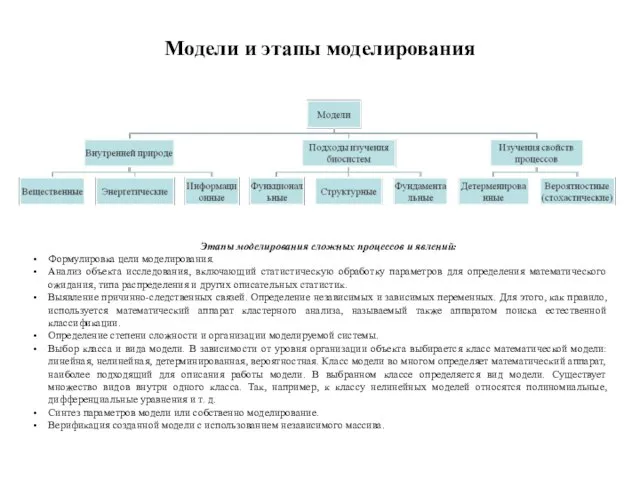
Модели и этапы моделирования
Этапы моделирования сложных процессов и явлений:
Формулировка цели моделирования.
Анализ объекта исследования, включающий статистическую обработку параметров для определения математического ожидания, типа распределения и других описательных статистик.
Выявление причинно-следственных связей. Определение независимых и зависимых переменных. Для этого, как правило, используется математический аппарат кластерного анализа, называемый также аппаратом поиска естественной классификации.
Определение степени сложности и организации моделируемой системы.
Выбор класса и вида модели. В зависимости от уровня организации объекта выбирается класс математической модели: линейная, нелинейная, детерминированная, вероятностная. Класс модели во многом определяет математический аппарат, наиболее подходящий для описания работы модели. В выбранном классе определяется вид модели. Существует множество видов внутри одного класса. Так, например, к классу нелинейных моделей относятся полиномиальные, дифференциальные уравнения и т. д.
Синтез параметров модели или собственно моделирование.
Верификация созданной модели с использованием независимого массива.

Психологические модели
Модель И.П. Павлова
И.П. Павлов выделяет целостный механизм анализатора включающий: периферическое, промежуточное и центральное звенья, а также говорит о существовании высшей нервной деятельности, обладающей своими каналами получения информации, называя их первой и второй сигнальной системой.
К первой сигнальной системе он относил психические образы, которые возникают вследствие воздействия на организм физических раздражителей.
Ко второй сигнальной системе он относил речемыслительные процессы. В качестве второго сигнального раздражителя им рассматривался внешний социальный и вместе с тем физический агент. Таким агентом является слово, которое воспринимается с помощью анализаторов, но вместе с тем оно наполнено социальным содержанием.
Психические явления выступали как носители информации, как сигналы, включающие систему регуляции организма и поведения человека, а в качестве основного механизма системы регуляции он рассматривал образование рефлекса (или рефлекторной дуги), который в свою очередь был не чем иным, как результатом сигнализации.

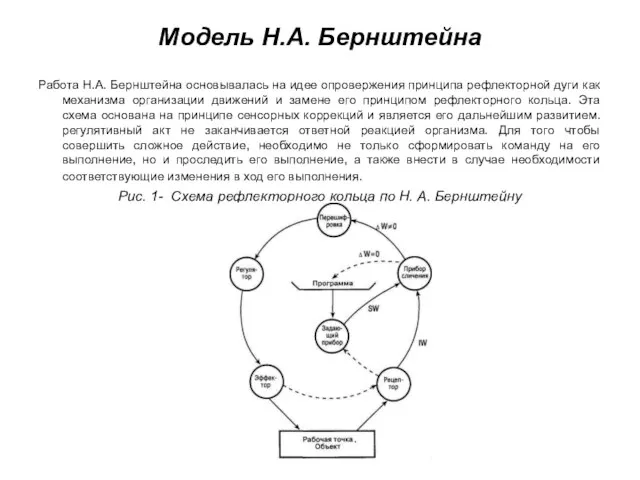
Модель Н.А. Бернштейна
Работа Н.А. Бернштейна основывалась на идее опровержения принципа рефлекторной дуги как механизма организации движений и замене его принципом рефлекторного кольца. Эта схема основана на принципе сенсорных коррекций и является его дальнейшим развитием. регулятивный акт не заканчивается ответной реакцией организма. Для того чтобы совершить сложное действие, необходимо не только сформировать команду на его выполнение, но и проследить его выполнение, а также внести в случае необходимости соответствующие изменения в ход его выполнения.
Рис. 1- Схема рефлекторного кольца по Н. А. Бернштейну

Модель К. Халла
Американский ученый К. Халл рассматривал живой организм как саморегулируемую систему со специфическими механизмами поведенческой и генетико-биологической регуляции. Эти механизмы большей частью врожденные и служат для поддержания оптимальных условий физического и биохимического равновесия в организме — гомеостаза — и включаются в действие тогда, когда это равновесие нарушено.

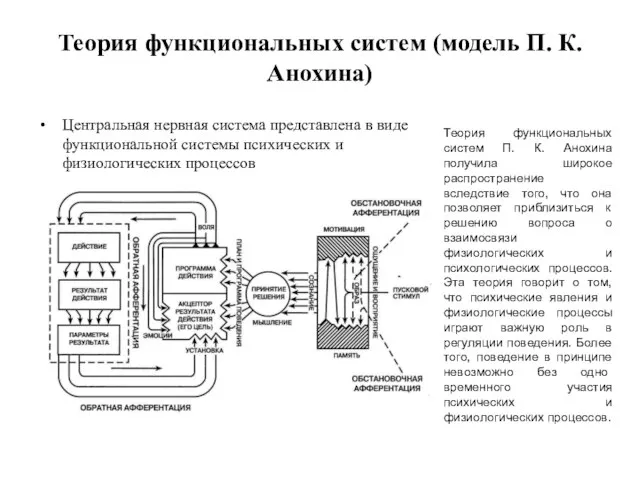
Теория функциональных систем (модель П. К. Анохина)
Центральная нервная система представлена в виде функциональной системы психических и физиологических процессов
Теория функциональных систем П. К. Анохина получила широкое распространение вследствие того, что она позволяет приблизиться к решению вопроса о взаимосвязи физиологических и психологических процессов. Эта теория говорит о том, что психические явления и физиологические процессы играют важную роль в регуляции поведения. Более того, поведение в принципе невозможно без одно­временного участия психических и физиологических процессов.

Модель А.Р. Лурии
Так, А. Р. Лурия предложил выделить анатомически относительно автономные блоки головного мозга, обеспечивающие функционирование психических явлений:
Первый блок предназначен для поддержания определенного уровня активности. Он включает ретикулярную формацию ствола мозга, глубинные отделы среднего мозга, структуры лимбической системы, медиобазальные отделы коры лобных и височных долей мозга.
Второй блок связан с познавательными психическими процессами и предназначен для процессов получения, переработки и хранения информации. Данный блок состоит из участков коры головного мозга, которые в основном располагаются в задних и височных отделах больших полушарий.
Третий блок обеспечивает функции мышления, поведенческой регуляции и самоконтроля. Структуры, входящие в данный блок, находятся в передних отде­лах коры головного мозга.

Системный подход
Система - множество элементов, находящихся в отношениях и связях друг с другом, которое образует определенную целостность, единство.
Признаки системы:
система обладает целостностью, все ее части служат достижению единой цели;
система является большой как с точки зрения разнообразия составляющих ее элементов, так и с точки зрения количества одинаковых частей;
система является сложной, что означает наличие большего количества связей между элементами как по вертикали, так и по горизонтали. Следовательно, изменение в каком - либо одном компоненте влечет за собой изменение в других;
независимо от сложности и размера система обладает чертами «черного ящика», их поведение в любой момент недетерминировано как в силу стохастической природы входных действий, так и внутреннего ее поведения;
большинство систем, и в первую очередь наиболее сложные системы, содержат элементы конкурентной ситуации, т.е. обязательно существуют элементы, которые стремятся уменьшить эффективность системы.

Кибернетика Н. Винера
Появление кибернетики как самостоятельного научного направления относится к 1948 г., когда американский ученый, профессор математики Массачусетского технологического института Норберт Винер (1894—1964 гг.) опубликовал книгу «Кибернетика, или Управление и связь в животном и машине». В этой книге Винер обобщил закономерности, относящиеся к системам управления различной природы — биологическим, техническим и социальным.
Название «кибернетика» происходит от греческого «кибернетес», что первоначально означало «рулевой», «кормчий», но впоследствии стало обозначать и «правитель над людьми».
Объектом кибернетики являются все управляемые системы. Системы, не поддающиеся управлению, в принципе, не являются объектами изучения кибернетики. Кибернетика вводит такие понятия, как кибернетический подход, кибернетическая система. Кибернетические системы рассматриваются абстрактно, вне зависимости от их материальной природы. Примеры кибернетических систем — автоматические регуляторы в технике, ЭВМ, человеческий мозг, биологические популяции, человеческое общество, человеко-машинные системы,индивидуальные человеко-машинные системы. Каждая такая система представляет собой множество взаимосвязанных объектов (элементов системы), способных воспринимать, запоминать и перерабатывать информацию, а также обмениваться ею. Кибернетика разрабатывает общие принципы создания систем управления и систем для автоматизации умственного труда.
Человек, один из самых сложных объектов реального мира, известных науке в настоящее время. Он не только самоактуализирующийся и саморегулируемый, но и саморазвивающийся объект. Его свойство как саморазвивающегося объекта состоит в том, что он в состоянии самостоятельно создавать и изменять программу своих действий.
Другое дело технические системы. В отличие от живого организма все можно оценить и исследовать с момента их создания. Можно установить закономерности их функционирования.

Теория сигналов является центральной в кибернетике. Ее основными понятиями являются управляющий контур и информация.
Управляющий контур — это система управления технического или биологического объекта, которая включает в себя ряд механизмов, обеспечивающих процесс управления от момента получения сигнала до выполнения соответствующего действия.
Принято разделять разомкнутые, или открытые, и замкнутые управляющие контуры.
К разомкнутым управляющим контурам относятся системы, способные лишь к ответному действию, заложенному программой, без ее корректировки.
Закрытый управляющий контур включает в себя структурные элементы, которые обеспечивают контроль над выполнением действия до его полного завершения, и при необходимости выполняют корректировку действия в зависимости от условий, в которых это действие выполняется.
Н. Винер считает, что живой организм управляется по общим принципам. Для этого у него есть все необходимое, вплоть до морфологического строения отдельных органов и систем. Например, такова морфология нейрона. Нейрон имеет функциональный блок входа информации — дендрит; центральный, интегрирующий блок — тело нейрона; блок выхода — аксон. Следовательно, морфологическое строение и функциональная организация живого организма имеют природную предрасположенность к тому, чтобы осуществлять саморегуляцию по общекибернетическим принципам.

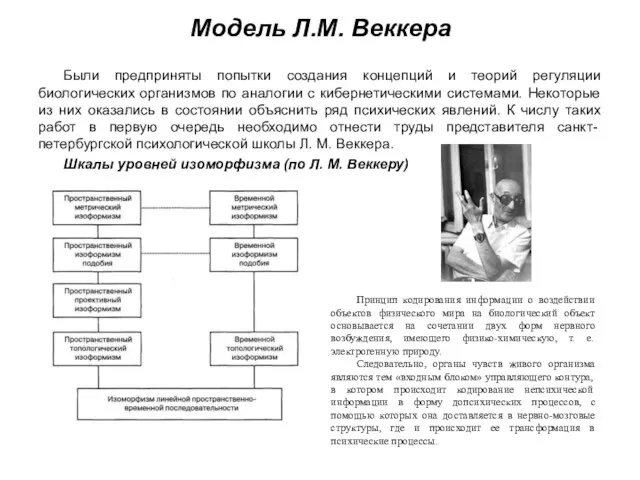
Модель Л.М. Веккера
Были предприняты попытки создания концепций и теорий регуляции биологических организмов по аналогии с кибернетическими системами. Некоторые из них оказались в состоянии объяснить ряд психических явлений. К числу таких работ в первую очередь необходимо отнести труды представителя санкт-петербургской психологической школы Л. М. Веккера.
Шкалы уровней изоморфизма (по Л. М. Веккеру)
Принцип кодирования информации о воздействии объектов физического мира на биологический объект основывается на сочетании двух форм нервного возбуждения, имеющего физико-химическую, т. е. электрогенную природу.
Следовательно, органы чувств живого организма являются тем «входным блоком» управляющего контура, в котором происходит кодирование непсихической информации в форму допсихических процессов, с помощью которых она доставляется в нервно-мозговые структуры, где и происходит ее трансформация в психические процессы.

Синергетика (Г. Хакена)
Хакен Герман (Hermann Haken, род. 12 июля 1927 г.) — немецкий физик-теоретик, основатель синергетики. Изучал физику и математику в университетах Галле (1946—1948) и Эрлангена (1948—1950), получив степени доктора философии и доктора естественных наук. С 1960 г. по 1995 г. являлся профессором теоретической физики университета Штутгарта[1]. До ноября 1997 г. был директором Института теоретической физики и синергетики университета Штутгарта. С 1995 г. является почетным профессором[1] и возглавляет Центр синергетики в этом институте, а также ведет исследования в Центре по изучению сложных систем в университете Флориды (Бока Рэтон, США). Основатель и редактор шпрингеровской серии по синергетике.
По Хакену, синергетика занимается изучением систем, состоящих из большого (очень большого, «огромного») числа частей, компонент или подсистем, одним словом, деталей, сложным образом взаимодействующих между собой. Слово «синергетика» и означает «совместное действие», подчеркивая согласованность функционирования частей, отражающуюся в поведении системы как целого.
Синергетический процесс самоорганизации материи это бесконечное чередование этапов «спокойной» адаптации и «революционных» перерождений, выводящих системы на новые ступени совершенства.

Общая теория систем Л. Фон Берталанфи
Карл Людвиг фон Берталанфи (англ. Ludwig von Bertalanffy; 19 сентября 1901, Вена — 12 июня 1972, Нью-Йорк) — австрийский биолог, постоянно проживавший в Канаде и США с 1949 года. Первооснователь обобщённой системной концепции под названием «Общая теория систем». Постановщик системных задач — прежде всего, в сфере разработки математического аппарата описания типологически несходных систем. Исследователь изоморфизма законов в различных сегментах научного знания.
Сам фон Берталанфи описывает происхождение общей теории систем как результат конфликта между механицизмом и витализмом. Обе точки зрения были для него неприемлемы: первая — как тривиальная, вторая — как вообще антинаучная.
Общая теория систем Л. Фон Берталанфи состоит в том, что если замкнутую систему вывести из состояния равновесия, то в ней начнутся процессы, возвращающие ее к состоянию термодинамического равновесия, в котором ее энтропия достигает максимального значения.
Со временем степень неравновесности будет уменьшаться, однако в любой момент времени ситуация будет неравновесной. В случае открытых систем отток энтропии наружу может уравновесить ее рост в самой системе. В этих условиях может возникнуть и поддерживаться стационарное состояние, такое состояние называется текущим равновесием. По своим характеристикам текущее равновесие может быть близко к равновесным состояниям.

Теория развития И.Р. Пригожина
Илья́ Рома́нович Приго́жин (фр. Ilya Prigogine; (12) 25 января 1917, Москва — 28 мая 2003, Брюссель) — бельгийский и американский физик и химик российского происхождения, лауреат Нобелевской премии по химии 1977 года, виконт Бельгии.
Основная масса работ И.Р. Пригожина посвящена неравновесной термодинамике и статистической механике необратимых процессов. Одно из главных достижений заключалось в том, что было показано существование неравновесных термодинамических систем, которые, при определённых условиях, поглощая вещество и энергию из окружающего пространства, могут совершать качественный скачок к усложнению (диссипативные структуры). Причём такой скачок не может быть предсказан, исходя из классических законов статистики. Такие системы позже были названы его именем. Расчёт таких систем стал возможен благодаря его работам, выполненным в 1947 году.
Теория развития И.Р. Пригожина гласит, что если отток энтропии (меры необратимого рассеяния энергии) превышает ее внутреннее производство, то возникают и разрастаются до макроскопического уровня крупномасштабные флуктуации. При определенных условиях в системе начинает происходить самоорганизация — создание упорядоченных структур из хаоса. Эти структуры могут последовательно переходить во все более сложные состояния.

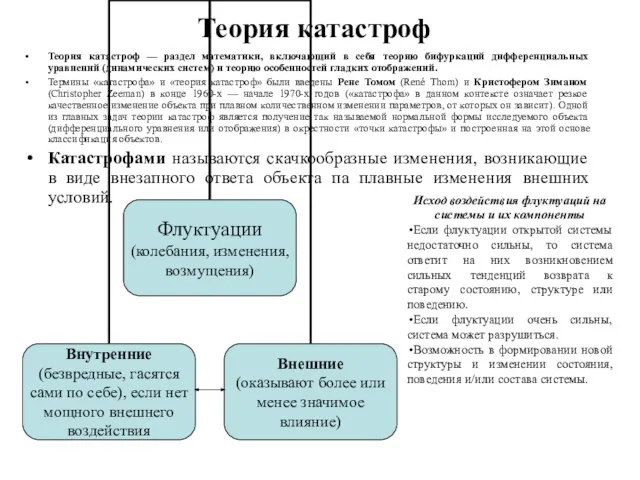
Теория катастроф
Теория катастроф — раздел математики, включающий в себя теорию бифуркаций дифференциальных уравнений (динамических систем) и теорию особенностей гладких отображений.
Термины «катастрофа» и «теория катастроф» были введены Рене Томом (René Thom) и Кристофером Зиманом (Christopher Zeeman) в конце 1960-х — начале 1970-х годов («катастрофа» в данном контексте означает резкое качественное изменение объекта при плавном количественном изменении параметров, от которых он зависит). Одной из главных задач теории катастроф является получение так называемой нормальной формы исследуемого объекта (дифференциального уравнения или отображения) в окрестности «точки катастрофы» и построенная на этой основе классификация объектов.
Катастрофами называются скачкообразные изменения, возникающие в виде внезапного ответа объекта па плавные изменения внешних условий.
Исход воздействия флуктуаций на системы и их компоненты
Если флуктуации открытой системы недостаточно сильны, то система ответит на них возникновением сильных тенденций возврата к старому состоянию, структуре или поведению.
Если флуктуации очень сильны, система может разрушиться.
Возможность в формировании новой структуры и изменении состояния, поведения и/или состава системы.

Системный анализ
Системный анализ - научная дисциплина, разрабатывающая общие принципы исследования сложных объектов с учетом их системного характера.
Этапы системного анализа любого объекта:
Постановка задачи - определение объекта исследования, по­становка целей, задание критериев для изучения объекта и управления им.
Выделение системы, подлежащей изучению, и ее структуризация.
Составление математической модели изучаемой системы: параметризация, установление зависимостей между введенными параметрами, упрощение описания системы путем выделения подсистем и определения их иерархии, окончательная функция целей и критериев.
Применение системного анализа целесообразно прежде всего при решении сложных проблем управления — сложных в том смысле, что требует выбора наилучших альтернатив в условиях неполноты информации, неопределенности и т. п.

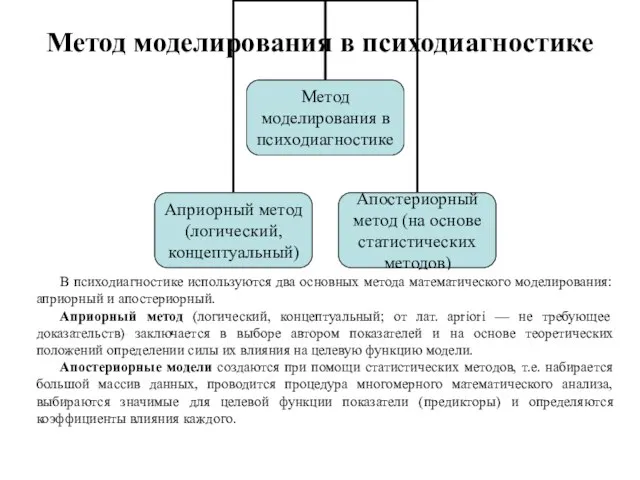
Метод моделирования в психодиагностике
В психодиагностике используются два основных метода математического моделирования: априорный и апостериорный.
Априорный метод (логический, концептуальный; от лат. apriori — не требующее доказательств) заключается в выборе автором показателей и на основе теоретических положений определении силы их влияния на целевую функцию модели.
Апостериорные модели создаются при помощи статистических методов, т.е. набирается большой массив данных, проводится процедура многомерного математического анализа, выбираются значимые для целевой функции показатели (предикторы) и определяются коэффициенты влияния каждого.