Математические модели и оптимальные процессы в макросистемах (термодинамика и экономика)

Макросистемы (МС)
Основная тематика ИЦ связана с исследованием оптимальных процессов и предельных возможностей макросистем с приложениями к необратимой термодинамике и экономике.
Макросистемы (МС) – системы, состоящие из большого числа индивидуально неуправляемых элементов (молекул в термодинамике, элементарных экономических агентов в экономике, индивидуумов в процессах миграции и пр.). Управление в таких системах возможно только на макроуровне, изменением воздействий, влияющих на все множество микроэлементов.

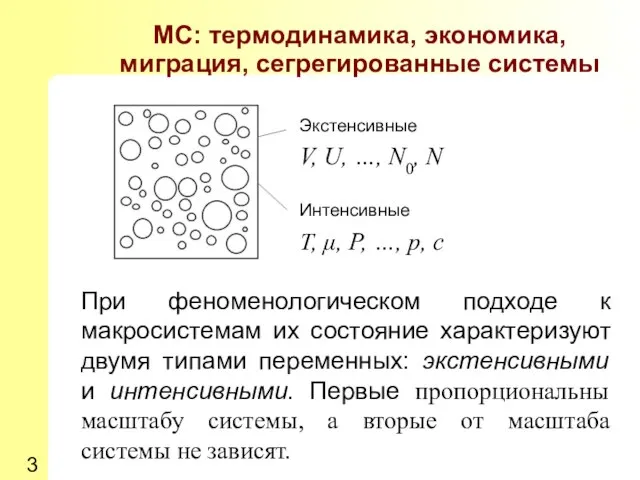
МС: термодинамика, экономика, миграция, сегрегированные системы
Экстенсивные
V, U, …, N0, N
Интенсивные
T, μ, P, …, p, c
При феноменологическом подходе к макросистемам их состояние характеризуют двумя типами переменных: экстенсивными и интенсивными. Первые пропорциональны масштабу системы, а вторые от масштаба системы не зависят.

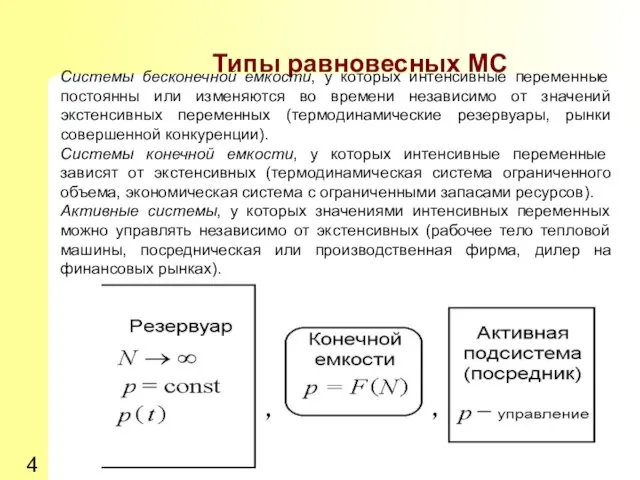
Типы равновесных МС
Системы бесконечной емкости, у которых интенсивные переменные постоянны или изменяются во времени независимо от значений экстенсивных переменных (термодинамические резервуары, рынки совершенной конкуренции).
Системы конечной емкости, у которых интенсивные переменные зависят от экстенсивных (термодинамическая система ограниченного объема, экономическая система с ограниченными запасами ресурсов).
Активные системы, у которых значениями интенсивных переменных можно управлять независимо от экстенсивных (рабочее тело тепловой машины, посредническая или производственная фирма, дилер на финансовых рынках).

Важной особенностью макросистем является то обстоятельство, что при их взаимодействии возникают процессы обмена, приводящие к возникновению потоков, которые изменяют экстенсивные переменные систем так, что в системах конечной емкости интенсивные переменные выравниваются. Эти «естественные» процессы протекают без какого-либо воздействия окружающей среды. Для возврата контактировавших систем в исходное состояние требуется привлечение из окружения некоторого ресурса. Такие процессы называют необратимыми.
Одной из характеристик макросистем является количественная мера необратимости процессов, изменение которой характеризует тот объем ресурса, который потребуется привлечь для возврата макросистем в исходное состояние после необратимого процесса. В термодинамике мерой необратимости является энтропия, в экономике - функция благосостояния, на которой мы ниже остановимся подробнее. И ту и другую далее будем обозначать через S. Для любого процесса в макросистеме мера необратимости не убывает, если же она возрастает, то скорость ее роста называют диссипацией.

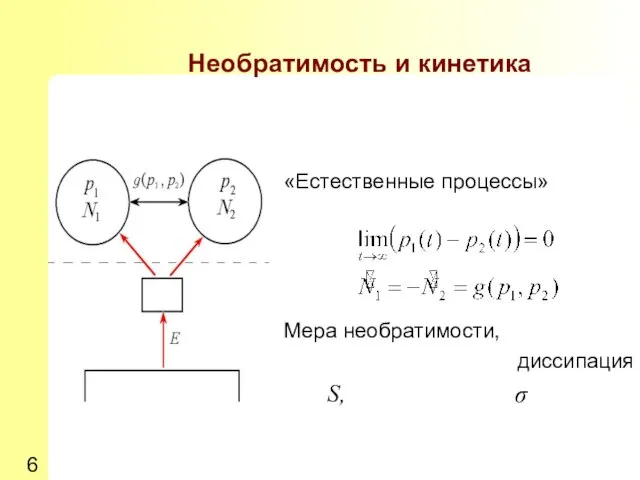
«Естественные процессы»
Мера необратимости,
диссипация
S, σ
Необратимость и кинетика

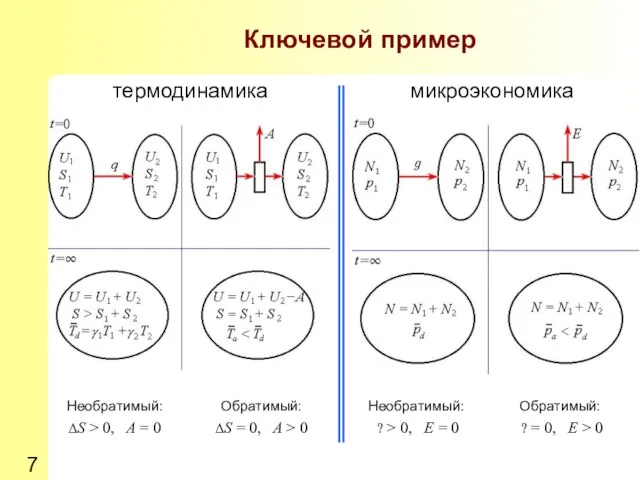
Ключевой пример
термодинамика микроэкономика

Основные задачи
Процессы минимальной диссипации .
Стационарное состояние ОС, включающей посредника.
Предельные возможности посредника в замкнутых, открытых и нестационарных МС.
Количественная мера необратимости в микроэкономике.
Область реализуемых состояний МС.

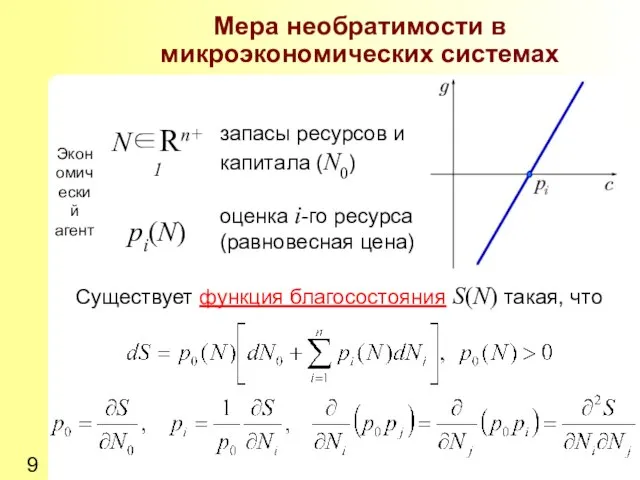
Мера необратимости в микроэкономических системах
Существует функция благосостояния S(N) такая, что

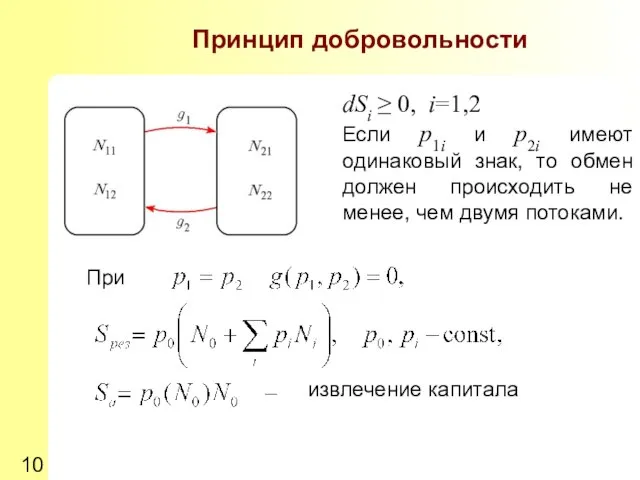
При
извлечение капитала
Принцип добровольности
dSi ≥ 0, i=1,2
Если p1i и p2i имеют одинаковый знак, то обмен должен происходить не менее, чем двумя потоками.

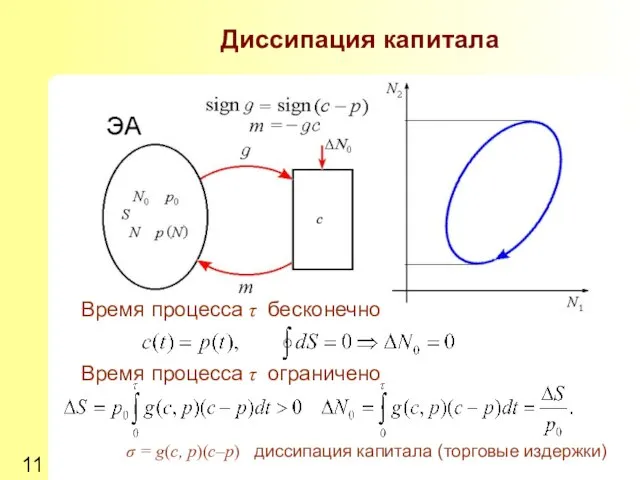
Диссипация капитала
Время процесса τ бесконечно
Время процесса τ ограничено
σ = g(c, p)(c–p) диссипация капитала (торговые издержки)

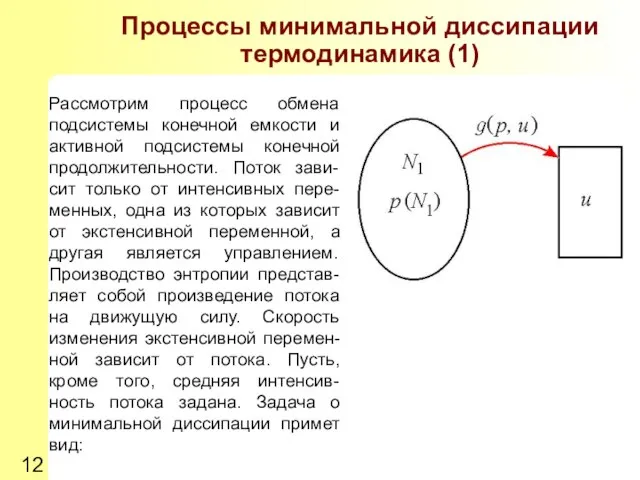
Процессы минимальной диссипации
термодинамика (1)
Рассмотрим процесс обмена подсистемы конечной емкости и активной подсистемы конечной продолжительности. Поток зави-сит только от интенсивных пере-менных, одна из которых зависит от экстенсивной переменной, а другая является управлением. Производство энтропии представ-ляет собой произведение потока на движущую силу. Скорость изменения экстенсивной перемен-ной зависит от потока. Пусть, кроме того, средняя интенсив-ность потока задана. Задача о минимальной диссипации примет вид:

Процессы минимальной диссипации
термодинамика (2)
Для случая
ϕ = α( p )g( p, u )
получим:

Процессы минимальной диссипации
термодинамика (3)
Теплоперенос:
p ~ T1, u ~ T2

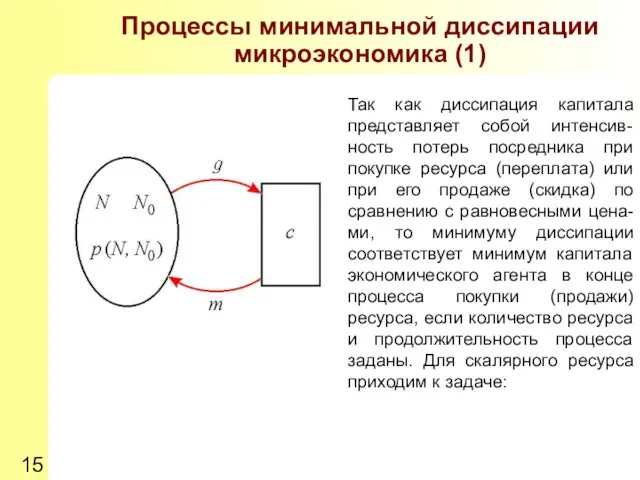
Процессы минимальной диссипации
микроэкономика (1)
Так как диссипация капитала представляет собой интенсив-ность потерь посредника при покупке ресурса (переплата) или при его продаже (скидка) по сравнению с равновесными цена-ми, то минимуму диссипации соответствует минимум капитала экономического агента в конце процесса покупки (продажи) ресурса, если количество ресурса и продолжительность процесса заданы. Для скалярного ресурса приходим к задаче:

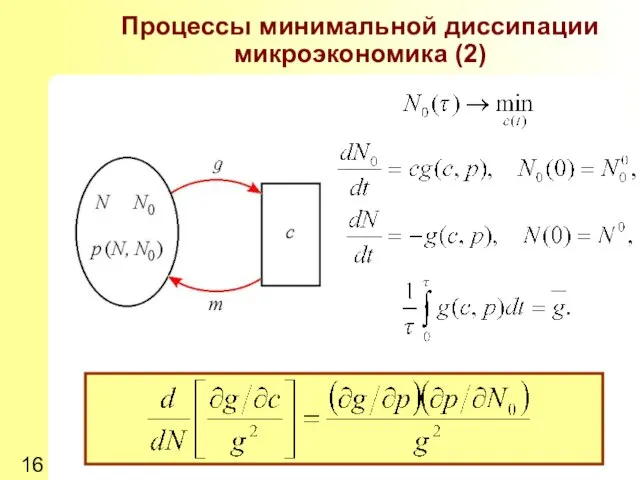
Процессы минимальной диссипации
микроэкономика (2)

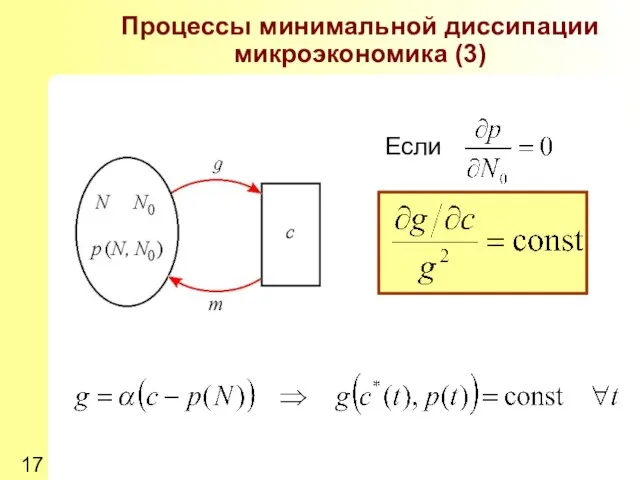
Процессы минимальной диссипации
микроэкономика (3)
Если

Стационарное состояние открытых МС (1)
Будем рассматривать открытую систему, состоящую из m внутренне равновесных подсистем, двух резервуаров и активной подсистемы. Между всеми подсистемами возникают потоки, зависящие от различия их интенсивных переменных, так что в целом система неравновесна.
В стационарном режиме потоки отличны от нуля, если число резервуаров больше двух и их интенсивные переменные различны. Для простоты рассмотрим систему с двумя резервуарами. Активная система может контактировать как с резервуарами, так и с любой из подсистем, устанавливая в точках контакта значения интенсивных переменных. Требуется выбрать такие значения переменных u, чтобы извлекаемый ею поток «организованной» энергии (работы, работы разделения, электрической энергии) был максимален.

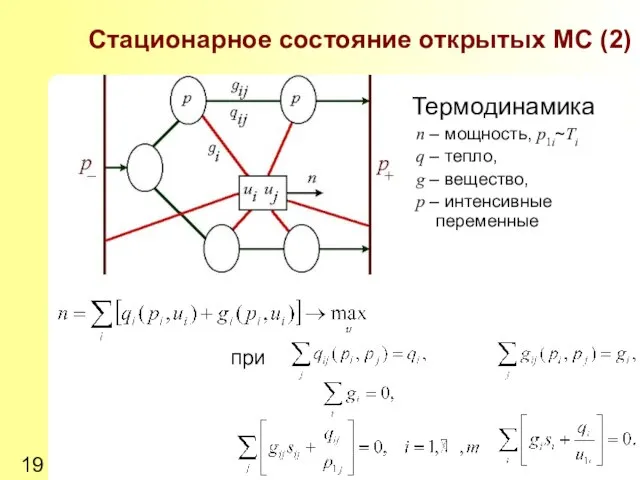
Стационарное состояние открытых МС (2)
Термодинамика
n – мощность, p1i~Ti
q – тепло,
g – вещество,
p – интенсивные переменные
при

Если g = 0, qij = αij(Ti – Tj), то
Если m = 2, T1 = T+, T2 = T–, то
Экстремальный принцип Пригожина при g = AX
(A – матрица Онзагера) справедлив для любого u.
– предельная мощность тепловой машины
Стационарное состояние открытых МС (3)

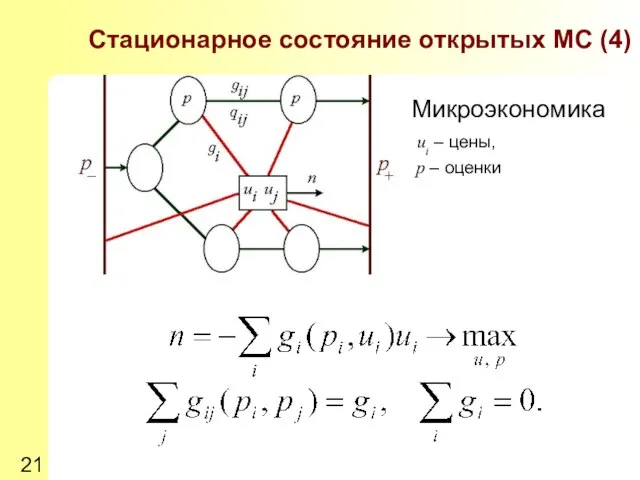
Стационарное состояние открытых МС (4)
Микроэкономика
ui – цены,
p – оценки

Аналог экстремального принципа Пригожина
для g = AΔ (Δij=pi – pj):
Матрица A – симметрическая.
Если gij = αij(pj – pj), gi = αi(ui – pj), то
Если m = 2, p1 = p+, p2 = p–, то
Стационарное состояние открытых МС (5)

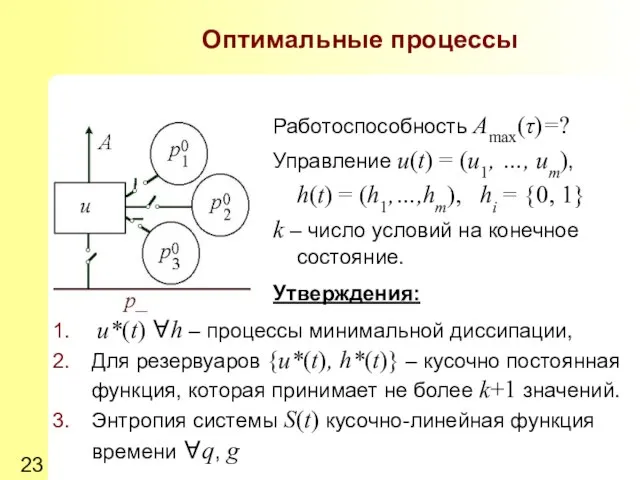
Оптимальные процессы
Работоспособность Amax(τ)=?
Управление u(t) = (u1, …, um),
h(t) = (h1,…,hm), hi = {0, 1}
k – число условий на конечное состояние.
Утверждения:
.u*(t) ∀h – процессы минимальной диссипации,
Для резервуаров {u*(t), h*(t)} – кусочно постоянная функция, которая принимает не более k+1 значений.
Энтропия системы S(t) кусочно-линейная функция времени ∀q, g

Если
– эксергия

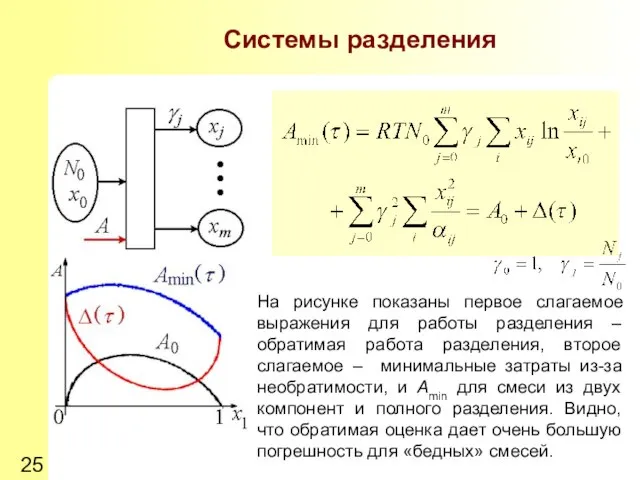
Системы разделения
На рисунке показаны первое слагаемое выражения для работы разделения – обратимая работа разделения, второе слагаемое – минимальные затраты из-за необратимости, и Amin для смеси из двух компонент и полного разделения. Видно, что обратимая оценка дает очень большую погрешность для «бедных» смесей.

Микроэкономика. Прибыльность =? (1)
Прибыльность – максимальный капитал, который можно извлечь в системе экономических агентов с разными начальными состояниями за время τ.
Заданы для каждого экономического агента начальные запасы ресурса, капитала и соответствующие им оценки. Система может включать или не включать резервуар. Посредник меняет цены закупок так, чтобы извлечь максимальную прибыль.

E∞ – аналог эксергии.
τ – задано:
c*(t) удовлетворяет условиям минимальной диссипации при каждом контакте
⇒
удовлетворяют условиям
Микроэкономика. Прибыльность =? (2)

Нестационарные резервуары (1)
Для нестационарного случая извлечение работы в термодинамике и прибыли в микроэкономике возможно при взаимодействии не с несколькими, а только с одной подсистемой. Мы остановимся только на этом случае, хотя решение найдено и для нескольких нестационарных подсистем.

Нестационарные резервуары (2)
Термодинамика
Микроэкономика

Область реализуемости (1)
Кроме прямых ограничений на состояние МС, наложенных в конкретной задаче, для этих систем характерны ограничения, возникающие из-за того, что в замкнутых системах показатель необратимости может только возрастать, а в открытых системах диссипация (энергии, капитала) неотрицательна.
Общая методология построения области реализуемости для замкнутых МС, включающих активные подсистемы, такова:
1. Записывают уравнения балансов, включая в их число балансовое соотношение по фактору необратимости S.
2. При ограничениях, наложенных на продолжительность процесса, находят минимальное значение σ = σmin, при котором может быть достигнуто то или иное состояние. Этому значению соответствует процесс минимальной диссипации.
3. Уравнения балансов при условии σ > σmin определяют область реализуемости D.

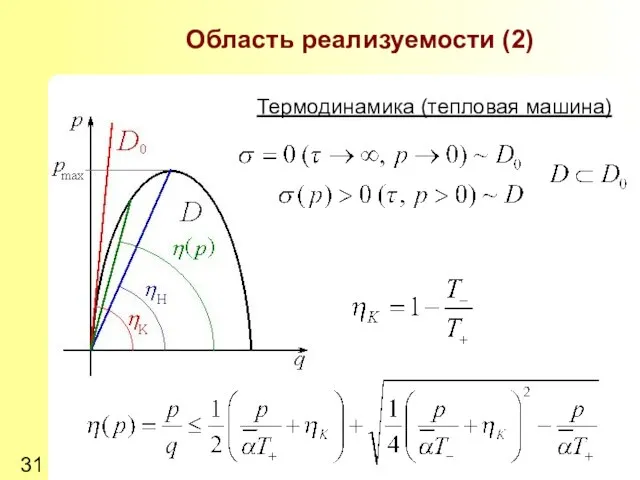
Область реализуемости (2)
Термодинамика (тепловая машина)

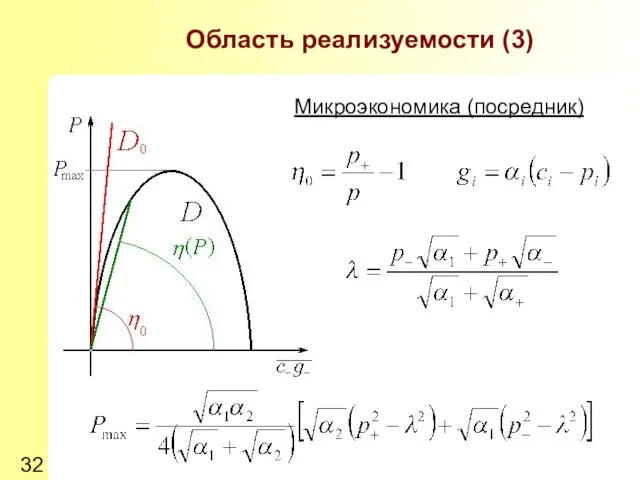
Область реализуемости (3)
Микроэкономика (посредник)