Слайд 2Компоненты динамической системы
Фазовое пространство X, элементы которого (“точки”) представляют собой возможные

состояния системы.
“Время”, которое может быть дискретным или непрерывным.
Закон эволюции системы.
Слайд 3Динамическая система – математическая модель некоторого мира
В начале XX века Пуанкаре

обнаружил невозможность явного описания форм траекторий точек пространства в общем случае
Это означает, что в общем случае динамическая система может вести себя «слишком» хаотично.
Слайд 4Инвариантные меры
Вместо описания орбиты каждой точки можно попытаться описать, как орбиты ведут

себя в среднем или изучать их асимптотическое поведение при устремлении времени к бесконечности.
Инвариантные меры представляют собой один из мощных способов описания асимптотических свойств систем со сложными структурами.
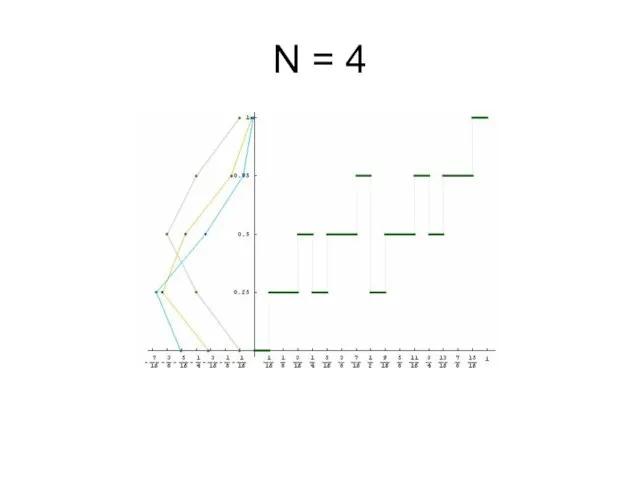
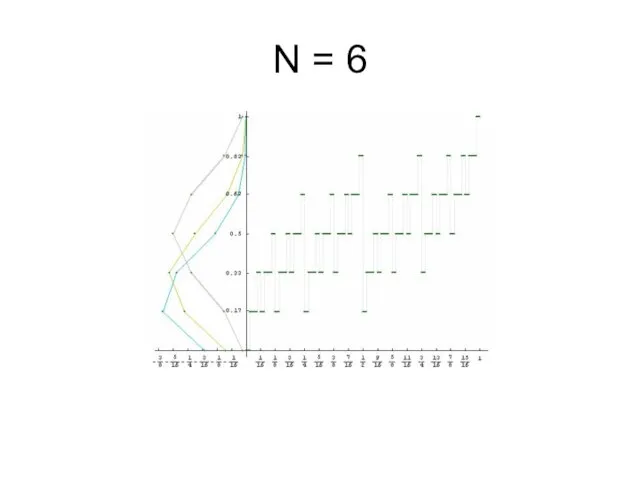
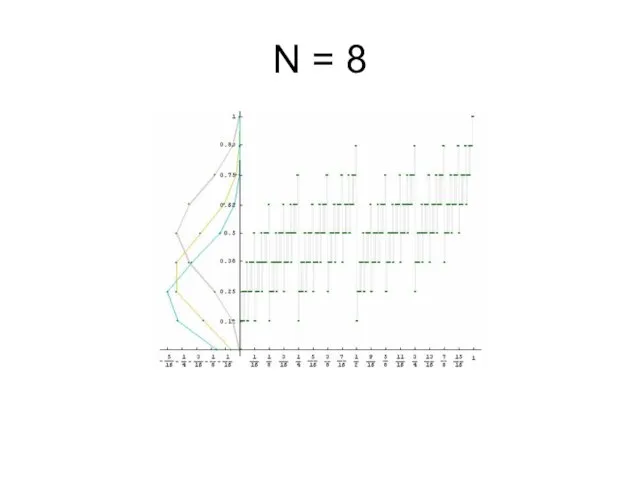
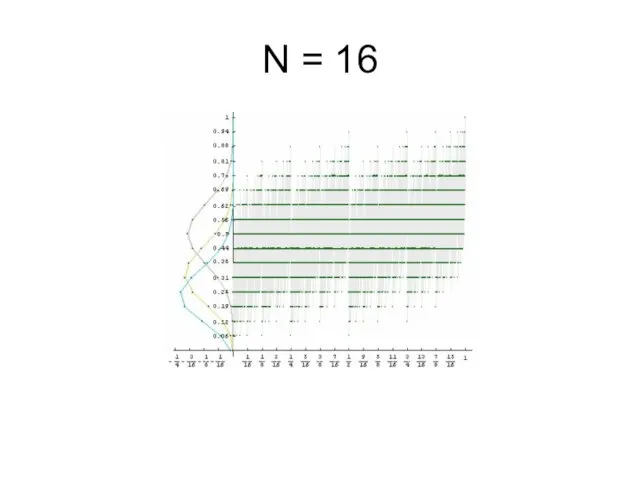
Слайд 5Компьютерное моделирование первых приближений плотностей мер μp
На графиках изображено распределение частоты

единиц в первых n знаках двоичного разложения чисел из отрезка [0, 1], а также первые приближения плотностей мер μp.




 Стипендия Правительства области
Стипендия Правительства области المالية االستدامة المالية
المالية االستدامة المالية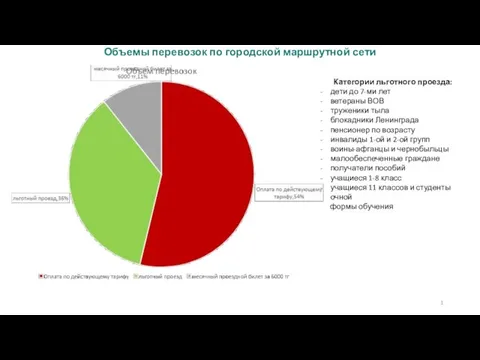 Объемы перевозок по городской маршрутной сети
Объемы перевозок по городской маршрутной сети День инвалида
День инвалида Презентация на тему Интернет и его возможности
Презентация на тему Интернет и его возможности Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5)
Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5) Культура Древней Греции
Культура Древней Греции Штриховая гладь
Штриховая гладь Профессия Повар-кондитер
Профессия Повар-кондитер Организационное стимулирование. Условия для внедрения мотивации персонала
Организационное стимулирование. Условия для внедрения мотивации персонала Что такое бенилюкс?
Что такое бенилюкс? Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс
Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс  FOOD SAFETY
FOOD SAFETY  Ассирия
Ассирия Презентация на тему Кометы и метеоры
Презентация на тему Кометы и метеоры Руководство Ernst&Young по составления бизнес-планов
Руководство Ernst&Young по составления бизнес-планов Куклы из махровых носков
Куклы из махровых носков Конституционные суды Приволжского Федерального округа
Конституционные суды Приволжского Федерального округа Японская каллиграфия - диалог культур Токио - Красноярск
Японская каллиграфия - диалог культур Токио - Красноярск «Пилот»: Маркетинг в компании
«Пилот»: Маркетинг в компании Устный журнал. В мире имён и названий
Устный журнал. В мире имён и названий Баскетбол. Тест по физической культуре
Баскетбол. Тест по физической культуре Материаловедение 5-6р
Материаловедение 5-6р Применение приборов серии IVS для решения задач вибродиагностики
Применение приборов серии IVS для решения задач вибродиагностики Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO
Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO Никола Тесла-повелитель молний
Никола Тесла-повелитель молний Проверка понимания озвученного текста
Проверка понимания озвученного текста Представление графической информации в компьютере
Представление графической информации в компьютере