Содержание
- 2. План Метод крупных вихрей для сжимаемой МГД турбулентности политропной плазмы. Метод крупных вихрей для сжимаемой МГД
- 3. Актуальность - Солнечная корона - Межзвездная/межпланетная среда Солнечная конвективная зона Магнитосфера Земли Инженерные применения - Звездный/солнечный
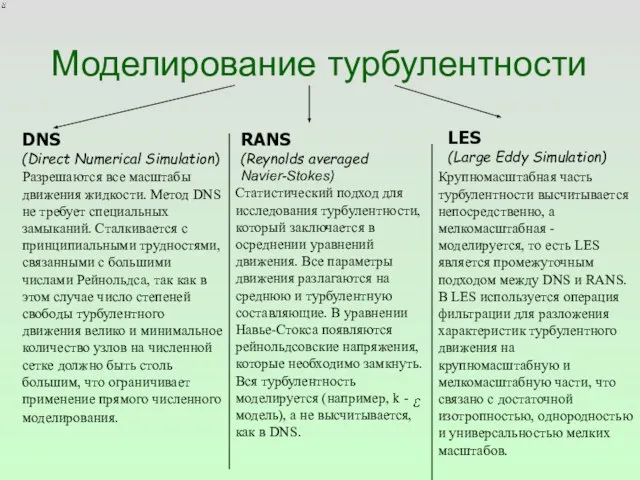
- 4. Моделирование турбулентности DNS (Direct Numerical Simulation) RANS (Reynolds averaged Navier-Stokes) LES (Large Eddy Simulation) Разрешаются все
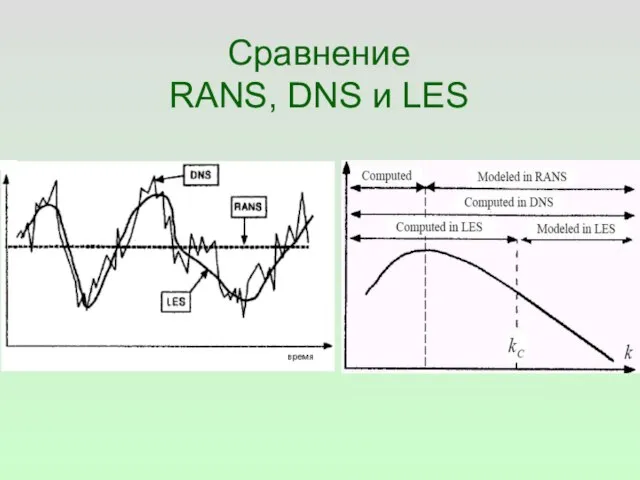
- 5. Сравнение RANS, DNS и LES
- 6. Метод крупных вихрей для сжимаемой МГД турбулентности политропной плазмы.
- 7. Уравнения МГД политропной плазмы - уравнение неразрывности уравнение импульсов - уравнение магнитной индукции Политропное соотношение:
- 8. Процедура фильтрации Турбулентное течение Крупномасштабное течение Мелкомасштабное течение функция фильтрации Условие нормировки: Свойства:
- 9. Виды фильтрационных функций 1.Гаусиановский фильтр 2.Фурье-фильтр 3.Цилиндрический фильтр
- 10. Отфильтрованные уравнения традиционным способом Дополнительные слагаемые, которые нужно параметризовать! Это требует дополнительные численные ресурсы
- 11. Процедура фильтрации - 2 Рассматривается сжимаемая жидкость, поэтому чтобы избежать появления дополнительных слагаемых в уравнениях после
- 12. Отфильтрованные уравнения МГД Subgrid scale (SGS) или Subfilter scale (SFS) В правой части уравнений - подсеточные
- 13. SGS Нелинейные члены должны быть записаны, используя крупномасштабные величины: Турбулентный тензор можно представить как: Леонардовский член
- 14. Подсеточное моделирование Условия реализуемости: - крупномасштабный тензор скорости деформации - крупномасштабный тензор магнитной ротации Модель вихревой
- 15. Расширенная модель Смагоринского для МГД Турбулентная вязкость: Турбулентная магнитная диффузия: - подсеточное замыкание для изотропной части
- 16. Расширенная модель Колмогорова для МГД Если длина фильтра находится в инерционном интервале, то можно предположить, что
- 17. Расширенная модель, основанная на перекрестной спиральности Определение перекрестной спиральности: (cross helicity) Перекрестная спиральность связана с обменом
- 18. Расширенная модель подобия масштабов для МГД Здесь неизвестные турбулентные тензоры моделируются в предположении, что они пропорциональны
- 19. Расширенная смешанная модель для МГД Расширенная смешанная модель является объединением двух моделей: расширенной модели Смагоринского и
- 20. Численная реализация Уравнения МГД в консервативной форме Конечно-разностные схемы 4го порядка точности Модифицированный метод Рунге-Кутта 3
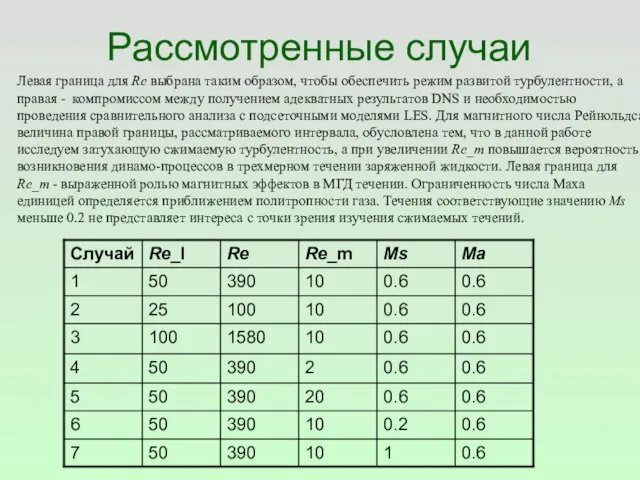
- 21. Рассмотренные случаи Левая граница для Re выбрана таким образом, чтобы обеспечить режим развитой турбулентности, а правая
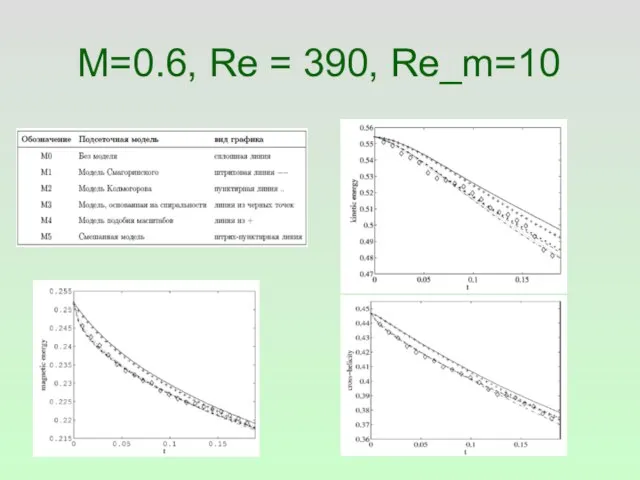
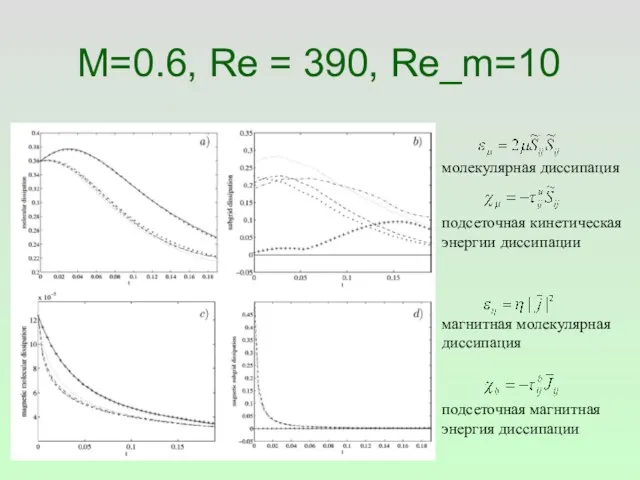
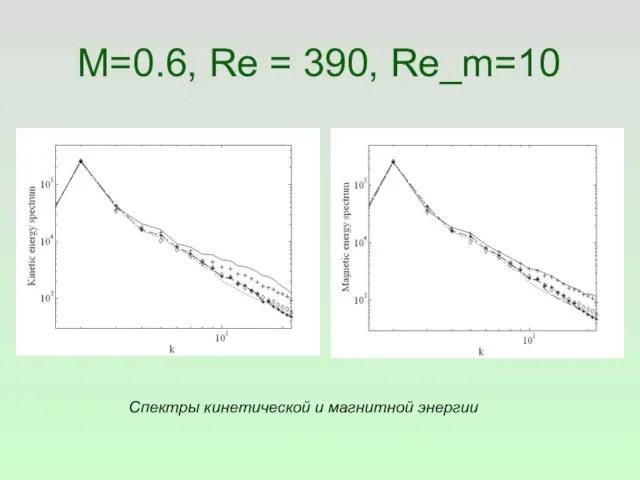
- 22. M=0.6, Re = 390, Re_m=10
- 23. M=0.6, Re = 390, Re_m=10 молекулярная диссипация подсеточная кинетическая энергии диссипации магнитная молекулярная диссипация подсеточная магнитная
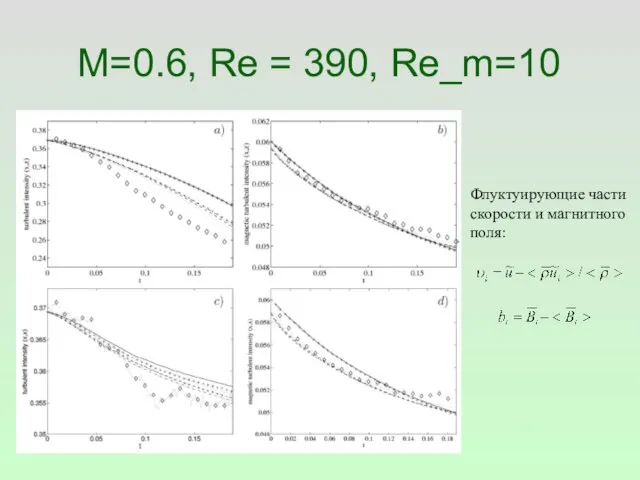
- 24. M=0.6, Re = 390, Re_m=10 Флуктуирующие части скорости и магнитного поля:
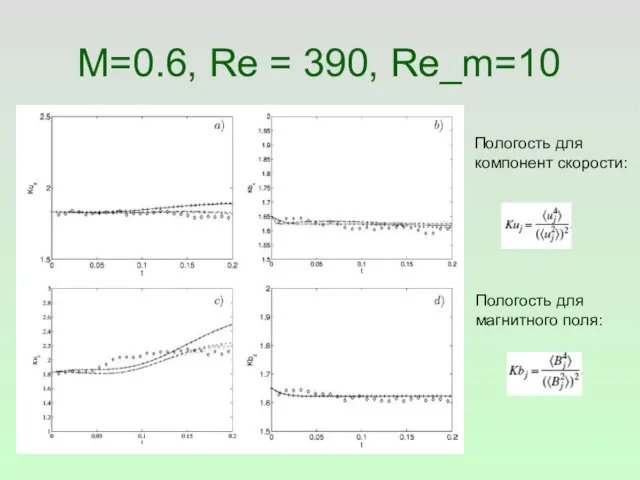
- 25. M=0.6, Re = 390, Re_m=10 Пологость для компонент скорости: Пологость для магнитного поля:
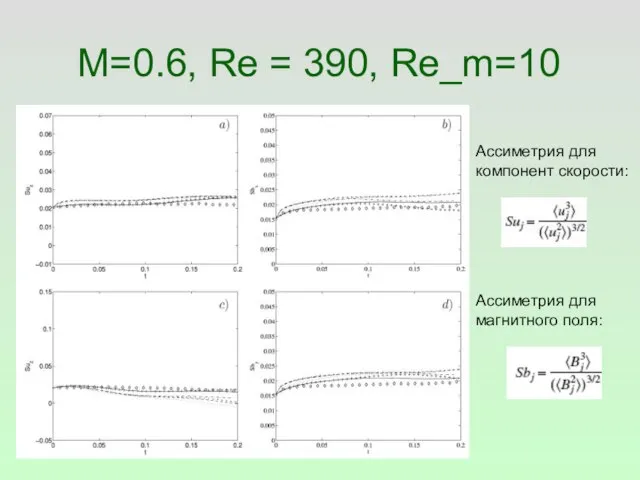
- 26. M=0.6, Re = 390, Re_m=10 Ассиметрия для магнитного поля: Ассиметрия для компонент скорости:
- 27. M=0.6, Re = 390, Re_m=10 Спектры кинетической и магнитной энергии
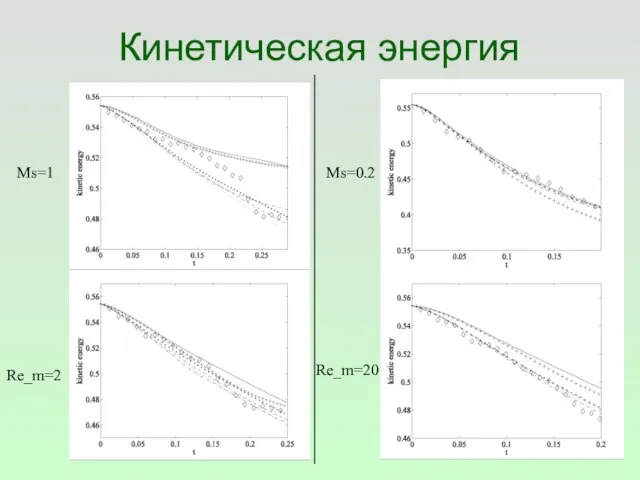
- 28. Кинетическая энергия Ms=1 Ms=0.2 Re_m=2 Re_m=20
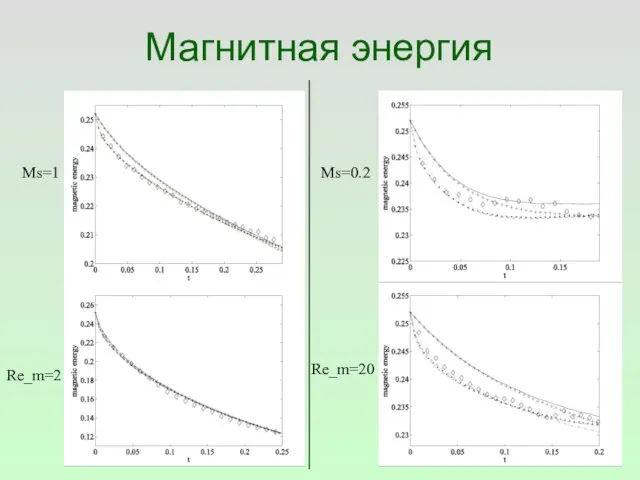
- 29. Магнитная энергия Ms=1 Ms=0.2 Re_m=2 Re_m=20
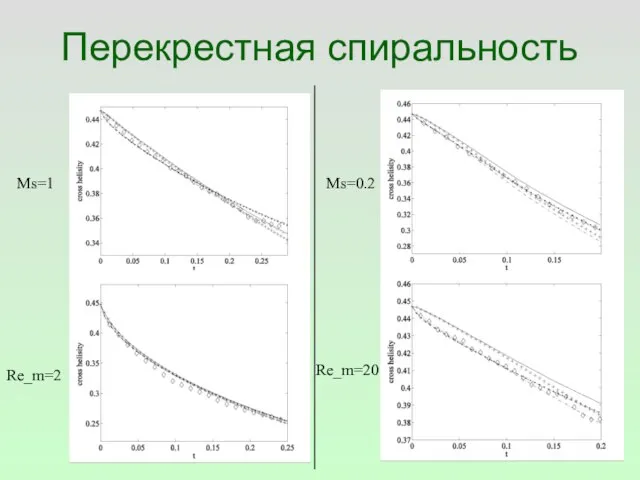
- 30. Перекрестная спиральность Ms=1 Ms=0.2 Re_m=2 Re_m=20
- 31. Выводы Метод LES сформулирован для сжимаемой МГД турбулентности для моделирования сжимаемой. Проведены численные исследования пяти подсеточных
- 32. Метод крупных вихрей для сжимаемой МГД турбулентности теплопроводящей плазмы.
- 33. Отфильтрованные уравнения МГД для теплопроводящей плазмы полная энергия внутренняя энергия Уравнение состояния:
- 34. Подсеточные слагаемые в отфильтрованных уравнениях - тензор подсеточных напряжений - магнитный подсеточный тензор напряжений - подсеточный
- 35. Подсеточные модели - 1 Для подсеточных тензоров в уравнениях импульса и индукции, используем модель Смагоринского для
- 36. Подсеточные модели - 2 Для окончательного замыкания полной системы уравнений сжимаемой магнитной гидродинамики необходимо параметризовать подсеточные
- 37. Подсеточные модели - 3 Сделаем замену индексов в корреляционном моменте третьего момента : Аналогичным образом запишем
- 38. Подсеточные модели - 4 Поэтому, сумму подсеточных тензоров Vj и Gj можно представить в следующем виде:
- 39. Рассмотренные случаи Так как эффекты сжимаемости и временная динамика температуры, определяемая из уравнения полной энергии, нетривиально
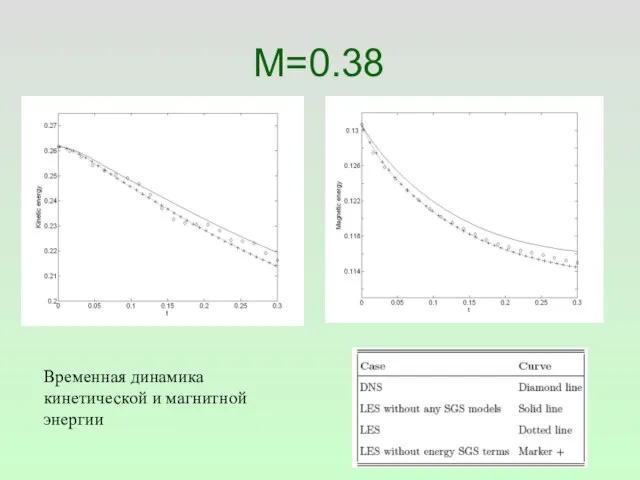
- 40. M=0.38 Временная динамика кинетической и магнитной энергии
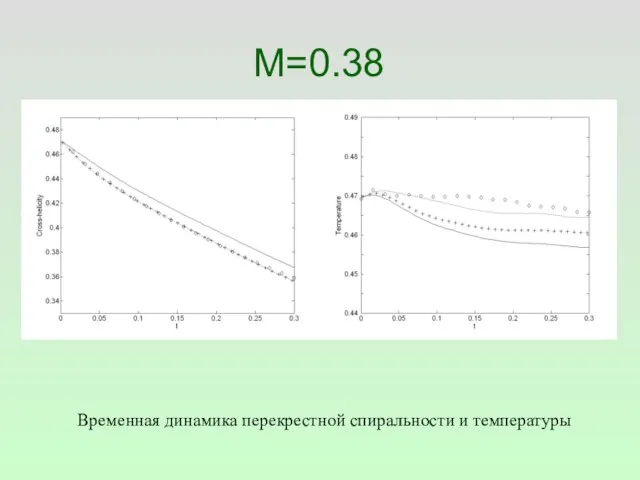
- 41. M=0.38 Временная динамика перекрестной спиральности и температуры
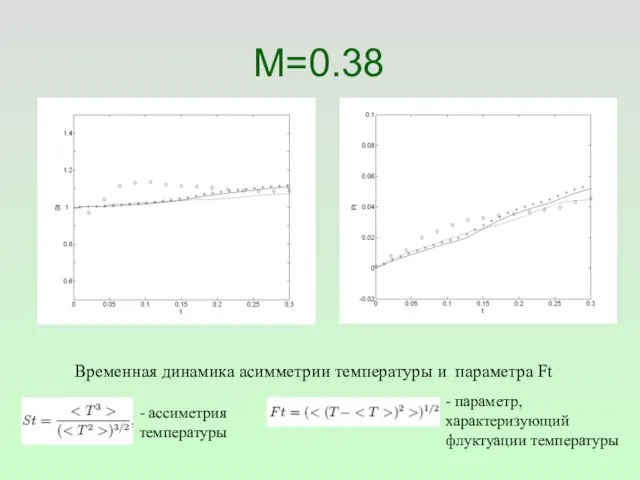
- 42. M=0.38 Временная динамика асимметрии температуры и параметра Ft - ассиметрия температуры - параметр, характеризующий флуктуации температуры
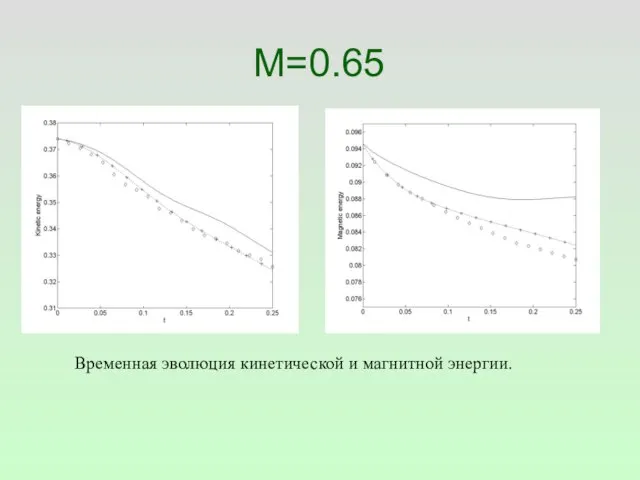
- 43. M=0.65 Временная эволюция кинетической и магнитной энергии.
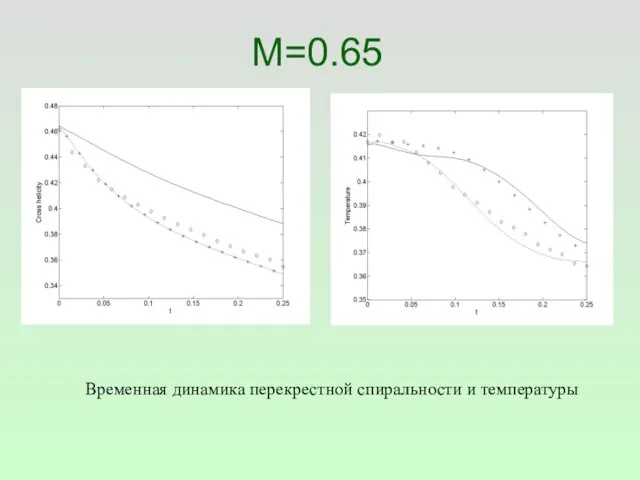
- 44. M=0.65 Временная динамика перекрестной спиральности и температуры
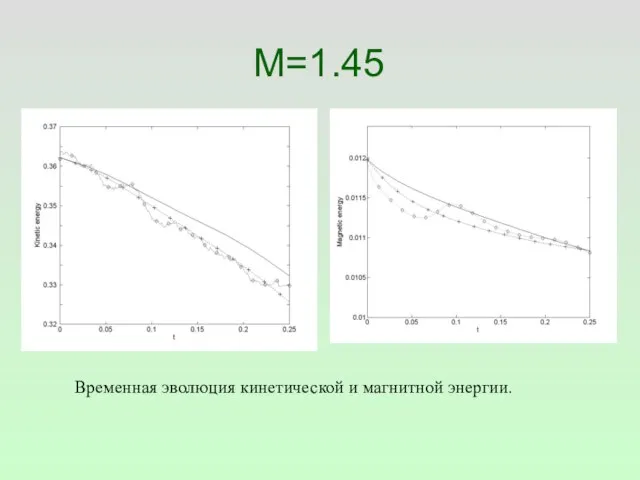
- 45. M=1.45 Временная эволюция кинетической и магнитной энергии.
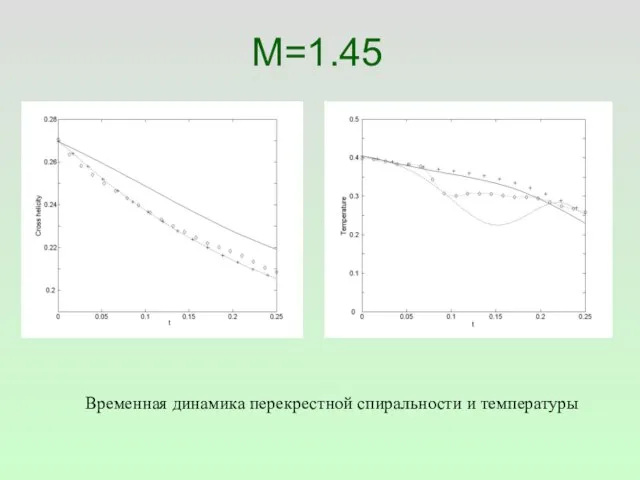
- 46. M=1.45 Временная динамика перекрестной спиральности и температуры
- 47. Выводы Получена система отфильтрованных уравнений МГД при наличии уравнения полной энергии. Предложены новые подсеточные модели для
- 48. Установление слабо сжимаемого режима в МГД турбулентности космической плазмы и свойства турбулентности локальной межзвёздной среды.
- 49. Локальная межзвездная среда Armstrong et al., ApJ (1995), 443:209-221 Спектр колмогоровского типа был теоретически получен для
- 50. МГД модель Статистически однородная, изотропная плазма в локальной межзвездной среде может быть описана одножидкостной магнитогидродинамической моделью:
- 51. Мелкомасштабные числа Маха Крупномасштабные значения чисел подобия: Мелкомасштабные значения чисел подобия: где Крупномасштабное течение, или постоянное
- 52. Параметры моделирования локальной межзвездной среды Для исследования локальной межзвездной турбулентности, используется LES метод для решения системы
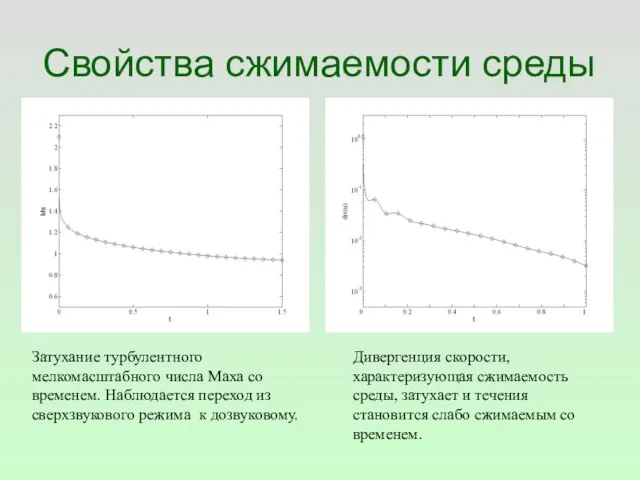
- 53. Свойства сжимаемости среды Затухание турбулентного мелкомасштабного числа Маха со временем. Наблюдается переход из сверхзвукового режима к
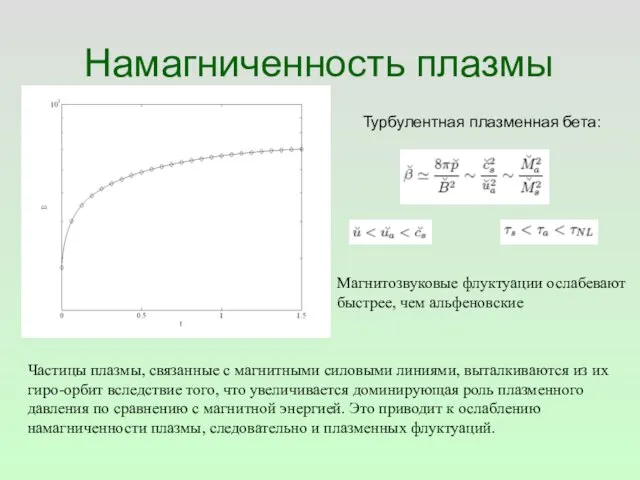
- 54. Намагниченность плазмы Турбулентная плазменная бета: Частицы плазмы, связанные с магнитными силовыми линиями, выталкиваются из их гиро-орбит
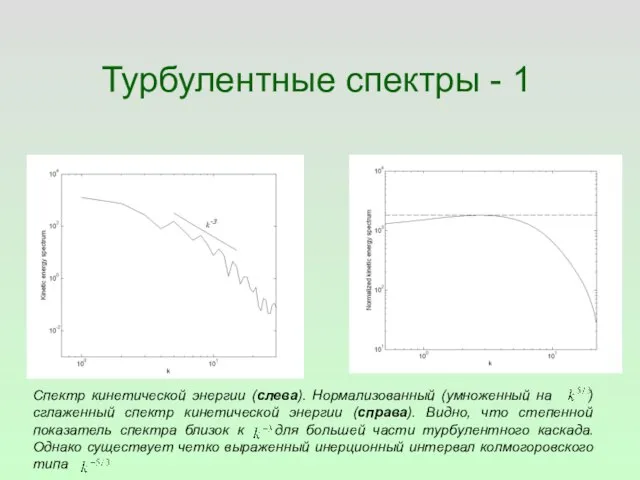
- 55. Турбулентные спектры - 1 Спектр кинетической энергии (слева). Нормализованный (умноженный на ) сглаженный спектр кинетической энергии
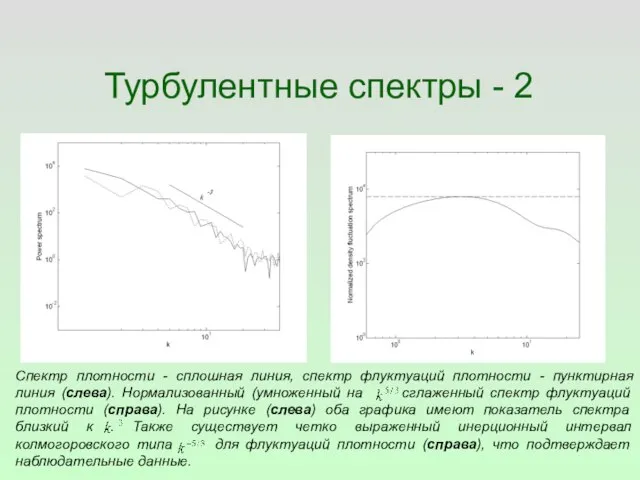
- 56. Турбулентные спектры - 2 Спектр плотности - сплошная линия, спектр флуктуаций плотности - пунктирная линия (слева).
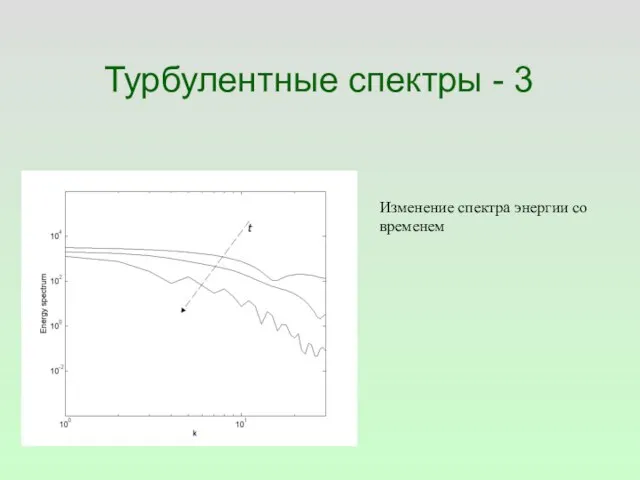
- 57. Турбулентные спектры - 3 Изменение спектра энергии со временем
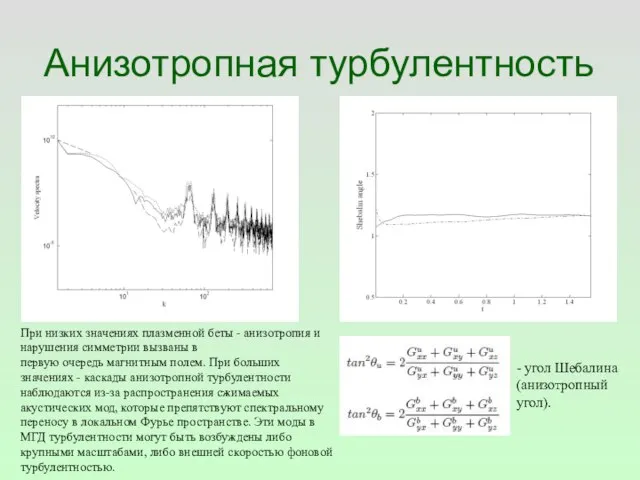
- 58. Анизотропная турбулентность - угол Шебалина (анизотропный угол). При низких значениях плазменной беты - анизотропия и нарушения
- 59. Выводы Флуктуации плотности являются пассивным скаляром в поле скорости в умеренно сжимаемой МГД турбулентности и демонстрируют
- 60. 1. Chernyshov A. A., Karelsky K. V., Petrosyan A. S. Subgrid-scale modeling in large-eddy simulations of
- 61. Спасибо за внимание!
- 62. Турбулентность широкий диапазон временных и пространственных масштабов нет аналитического решения нелинейность трехмерность нелинейное слагаемое >> диссипативное
- 63. SGS Нелинейные члены должны быть записаны, используя крупномасштабные величины: Турбулентный тензор можно представить как: Леонардовский член
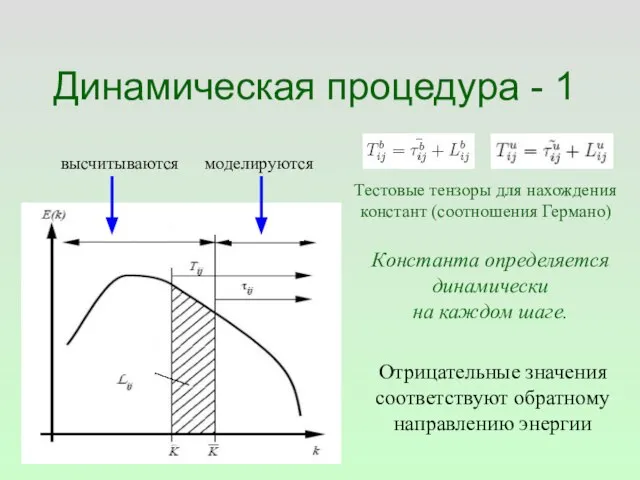
- 64. Динамическая процедура - 1 высчитываются моделируются Тестовые тензоры для нахождения констант (соотношения Германо) Константа определяется динамически
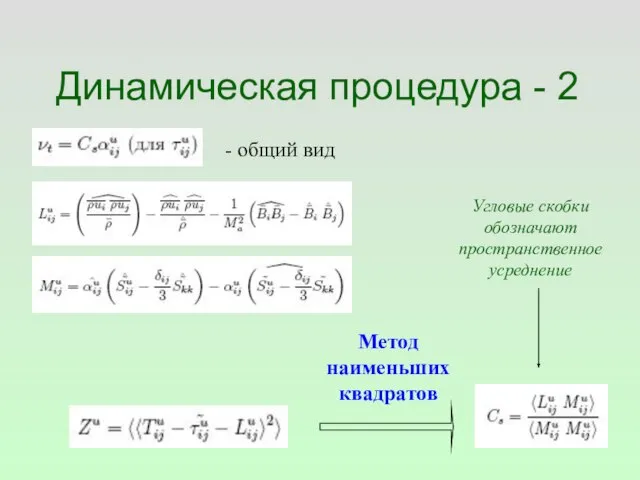
- 65. Динамическая процедура - 2 Метод наименьших квадратов Угловые скобки обозначают пространственное усреднение - общий вид
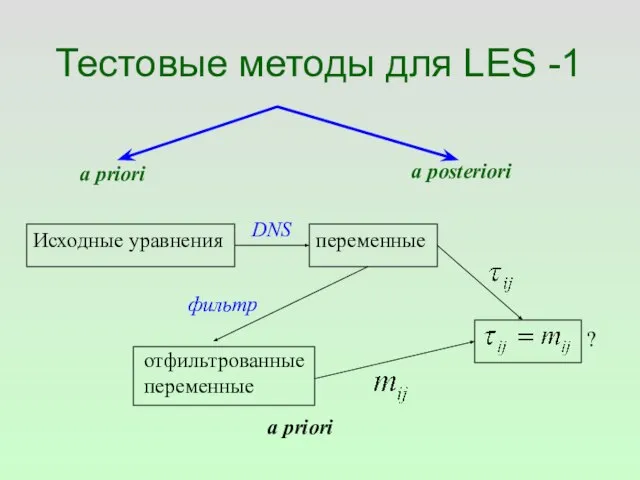
- 66. Тестовые методы для LES -1 a priori a posteriori Исходные уравнения переменные DNS отфильтрованные переменные фильтр
- 68. Скачать презентацию





































 Unusual traditions of birthday celebrations
Unusual traditions of birthday celebrations Автомобили контейнерые и контейнеры
Автомобили контейнерые и контейнеры Коррекционно-образовательное значение литературы в обучении школьников с ТНР
Коррекционно-образовательное значение литературы в обучении школьников с ТНР Муниципальное образовательное учреждение для детей дошкольного и младшего школьного возраста «Начальная школа – детский сад с.
Муниципальное образовательное учреждение для детей дошкольного и младшего школьного возраста «Начальная школа – детский сад с. Зевс. Бог неба, грома и молний, ведающий всем миром
Зевс. Бог неба, грома и молний, ведающий всем миром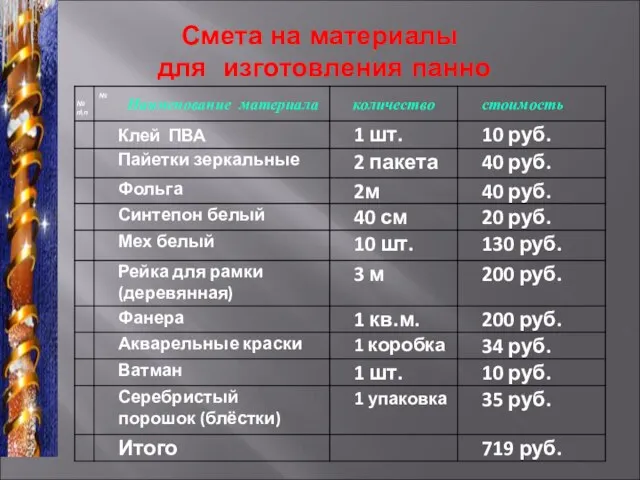 Смета на материалы для изготовления панно
Смета на материалы для изготовления панно Творческая биография А.Н. Бенуа
Творческая биография А.Н. Бенуа Ландшафтная архитектура
Ландшафтная архитектура Влияние Великой Отечественной войны на развитие химической науки. Вклад ученых-химиков в Победу.
Влияние Великой Отечественной войны на развитие химической науки. Вклад ученых-химиков в Победу. www.e-society.mk Ширењето на хакерскиот дух (интернет, слободен софтвер и нови медиуми) Новица Наков Слободен софтвер Македонија
www.e-society.mk Ширењето на хакерскиот дух (интернет, слободен софтвер и нови медиуми) Новица Наков Слободен софтвер Македонија Презентация на тему Риск. Виды рисков, методы нейтрализации рисков
Презентация на тему Риск. Виды рисков, методы нейтрализации рисков  Оптика 11 класс
Оптика 11 класс Популяризация театра
Популяризация театра Молекулярные машины
Молекулярные машины Confusing words: rubbish, garbage, trash, litter, waste, junk, debris
Confusing words: rubbish, garbage, trash, litter, waste, junk, debris Certificate
Certificate Домик из фруктов
Домик из фруктов Перестановка слагаемых (1 класс)
Перестановка слагаемых (1 класс) Eastern cousine
Eastern cousine ВКР: Выбор варианта доставки крупногабаритной строительной техники из республики Корея в Российскую Федерацию
ВКР: Выбор варианта доставки крупногабаритной строительной техники из республики Корея в Российскую Федерацию Методика применения электронного учебного пособияпо базовому курсу информатики Руководитель проекта: Огарков А.Ю., учитель инфо
Методика применения электронного учебного пособияпо базовому курсу информатики Руководитель проекта: Огарков А.Ю., учитель инфо АКЦИЯ «ТЕРРИТОРИЯ ЗДОРОВОГО ПИТАНИЯ» в г.Новосибирске 2009г.
АКЦИЯ «ТЕРРИТОРИЯ ЗДОРОВОГО ПИТАНИЯ» в г.Новосибирске 2009г. Избирательная система в РФ
Избирательная система в РФ Тестоделители и тестоокруглители
Тестоделители и тестоокруглители Crm. Клиентские исследования. Управление поведением. Лояльность
Crm. Клиентские исследования. Управление поведением. Лояльность Тоннелдегі бұрғылауаттыру жұмыстарын маркшейдерлік жұмыспен қамтамасыз ету
Тоннелдегі бұрғылауаттыру жұмыстарын маркшейдерлік жұмыспен қамтамасыз ету Семейство Бобовые и Пасленовые
Семейство Бобовые и Пасленовые Spraw, abyśmy wrócili do Twojej jedności
Spraw, abyśmy wrócili do Twojej jedności