Содержание
- 2. Введение в теорию политической конкуренции Участники: Избиратели Партии Кандидаты СМИ Группы интересов Ограничения: Число партий Бюджет
- 3. Модель Хотеллинга-Даунса (1957) Партии формулируют политику для того, чтобы выиграть выборы, а не выигрывают выборы для
- 4. Причины ненаблюдаемости схождения платформ Поддержка кандидатом определенной идеологии – деление всех полити-ков на office-seeking (Hotelling-Downs, 1957)
- 5. Безразличие и отчуждение Безразличие: избиратель голосует только тогда, когда В противном случае позиции кандидатов настолько близки,
- 6. Многомерная шкала предпочтений На практике трудно представить себе одномерную шкалу предпочтений: права человека, налоги, пенсии, протекционизм,
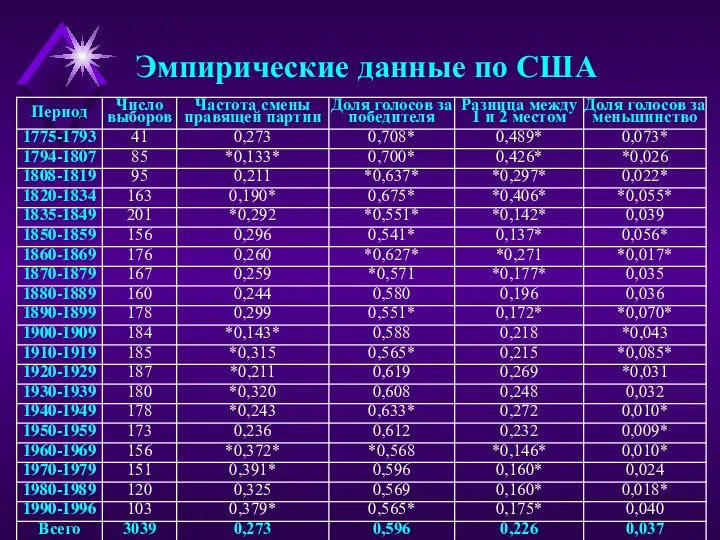
- 7. Эмпирические данные по США
- 8. Гипотезы зацикливания, случайности и заговора Поскольку процесс стабилен, предположим, что кандидаты делают выбор не из всего
- 9. Незакрытое множество Незакрытое множество – множество всех точек y внутри множества осущест-вимых альтернатив S, таких что
- 10. Иллюстрации к теореме Мак-Келви
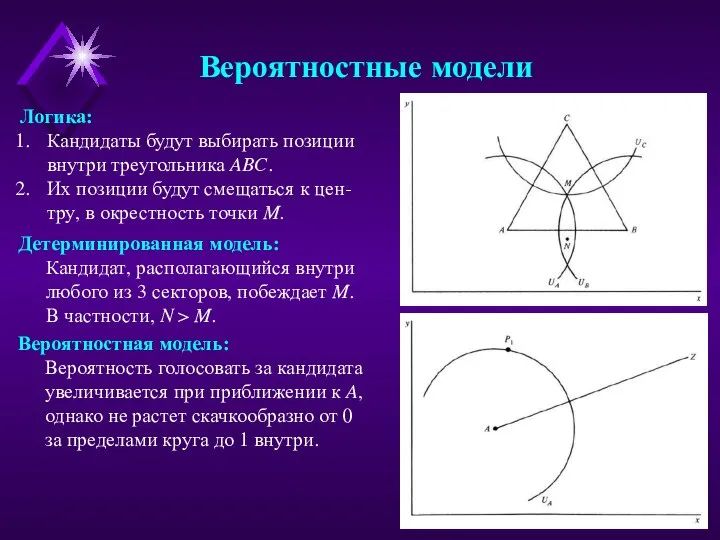
- 11. Вероятностные модели Логика: Кандидаты будут выбирать позиции внутри треугольника ABC. Их позиции будут смещаться к цен-тру,
- 12. Постановка модели: – выигрыши i-избирателя от победы 1-го и 2-го кандидатов, Пример: – вероятности голосования i-избирателя
- 13. Численный пример для функции ОБ Бентама: Если вероятностная реакция всех избирателей на различия между ожидаемыми полезностями
- 14. Модели с меняющейся валентностью Необъяснимые предыдущими моделями факты: Поляризация кандидатов (подтверждается по итогам голосований). Уменьшение числа
- 15. Численный пример Континуум избирателей, равномерно распределенных на [0; 1]. – критический избиратель. Левые голосуют за кандидата
- 16. Дальнейшее изучение моделей политической конкуренции Финансирование избирательной компании. Лоббирование. Группы интересов и модели их поведения. Равновесия
- 18. Скачать презентацию











![Численный пример Континуум избирателей, равномерно распределенных на [0; 1]. – критический избиратель.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1004129/slide-14.jpg)

 Анализ простоя местных вагонов
Анализ простоя местных вагонов Основные направления деятельности отдела по назначению, выплате пособий на детей и оказанию государственной социальной помощи
Основные направления деятельности отдела по назначению, выплате пособий на детей и оказанию государственной социальной помощи Состав правонарушения: понятие, элементы, виды
Состав правонарушения: понятие, элементы, виды Клод Моне
Клод Моне ИРЦ по модели «Информационно – культурный центр как средство для обеспечения доступности и открытости образования»
ИРЦ по модели «Информационно – культурный центр как средство для обеспечения доступности и открытости образования» Цифровой ввод (подключение кнопки). Лабораторное занятие 3
Цифровой ввод (подключение кнопки). Лабораторное занятие 3 Обработка природного материала
Обработка природного материала Феникс романтизма Задание на урок: Сформулируйте отличительные черты романтизма
Феникс романтизма Задание на урок: Сформулируйте отличительные черты романтизма Конструкции, грамматически не связанные с членами предложения
Конструкции, грамматически не связанные с членами предложения Великолепная семёрка
Великолепная семёрка Учитель – не профессия, а образ жизни: памятники учителям
Учитель – не профессия, а образ жизни: памятники учителям Игра Городки
Игра Городки Ты и твоя будущая профессия
Ты и твоя будущая профессия Животные и среда их обитания. Питание животных
Животные и среда их обитания. Питание животных МАЛАЯ УНИВЕРСИАДА г.Набережные Челны 2012г.
МАЛАЯ УНИВЕРСИАДА г.Набережные Челны 2012г. Презентация на тему Синие горы Кавказа в жизни и творчестве М.Ю. Лермонтова
Презентация на тему Синие горы Кавказа в жизни и творчестве М.Ю. Лермонтова  Дистанционный Кадавер курс
Дистанционный Кадавер курс Современные средства анализа эффективности интернет-маркетинга Фёдор Вирин, директор по исследованиям, Mail.ru.
Современные средства анализа эффективности интернет-маркетинга Фёдор Вирин, директор по исследованиям, Mail.ru. Коллигативные
Коллигативные Принятие христианства на Руси: исторические сведения
Принятие христианства на Руси: исторические сведения Я и моя семья
Я и моя семья COVER IDEAS-FINAL
COVER IDEAS-FINAL Черная металлургия мира
Черная металлургия мира С о в р е м е н н ы е к а д р о в ы е т е х н о л о г и и(п е р с о н а л – т е х н о л о г и и)
С о в р е м е н н ы е к а д р о в ы е т е х н о л о г и и(п е р с о н а л – т е х н о л о г и и) Архивно-логистический центр Сбербанка России
Архивно-логистический центр Сбербанка России Правописание сочетаний в русском языке
Правописание сочетаний в русском языке Immigration issues in europe
Immigration issues in europe Оформление проездного документа по талону Федеральной службы страхования
Оформление проездного документа по талону Федеральной службы страхования