Содержание
- 2. Что такое “модели смертности”? Два типа моделей 1. Эмпирические (описательные) модели Количественные закономерности смертности “законы смертности”
- 3. Зачем нужны модели смертности? 1. Обнаружить и компенсировать возможные дефекты собранных данных - Борьба с неполнотой
- 4. Эмпирические (описательные) модели Три закона смертности: Закон Гомпертца-Мейкхема Компенсационный закон смертности Замедление роста смертности в старших
- 5. Интенсивность смертности Определение
- 6. Эмпирическая оценка Сэчера для интенсивности смертности
- 7. Связь интенсивности смертности с вероятностью смерти μ(x) ≈ -ln(1 - qx)
- 8. Закон Гомпертца-Мейкхема μ(x) = A + R e αx A – компонента Мейкхема или фоновая смертность
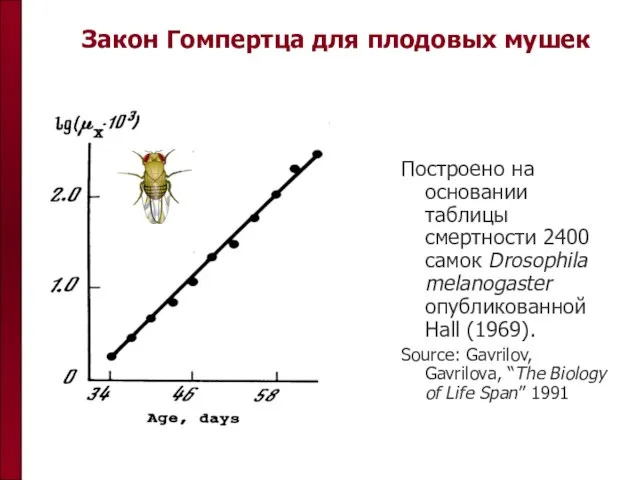
- 9. Закон Гомпертца для плодовых мушек Построено на основании таблицы смертности 2400 самок Drosophila melanogaster опубликованной Hall
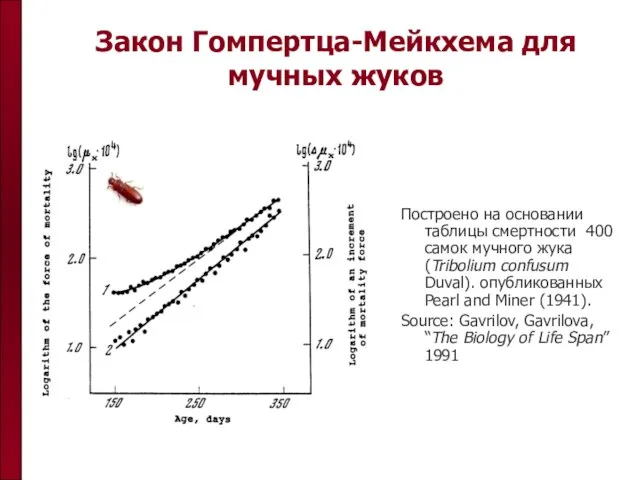
- 10. Закон Гомпертца-Мейкхема для мучных жуков Построено на основании таблицы смертности 400 самок мучного жука (Tribolium confusum
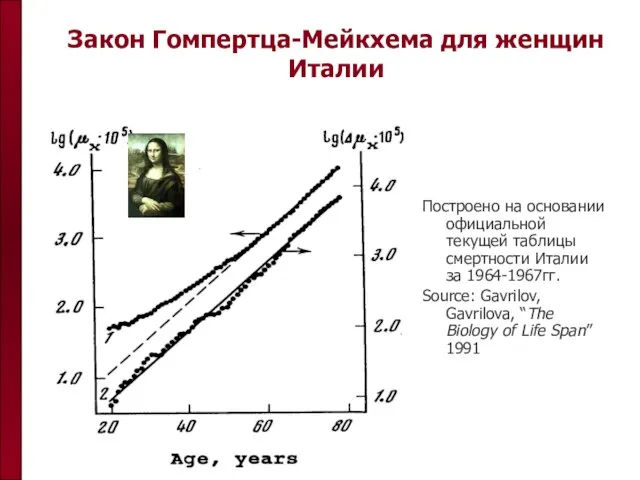
- 11. Закон Гомпертца-Мейкхема для женщин Италии Построено на основании официальной текущей таблицы смертности Италии за 1964-1967гг. Source:
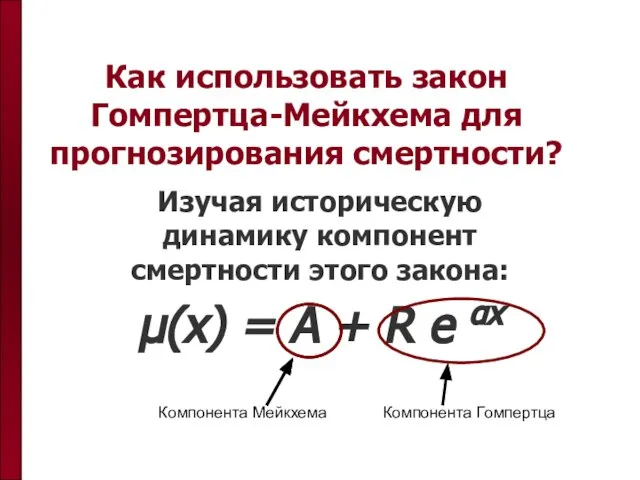
- 12. Как использовать закон Гомпертца-Мейкхема для прогнозирования смертности? Изучая историческую динамику компонент смертности этого закона: μ(x) =
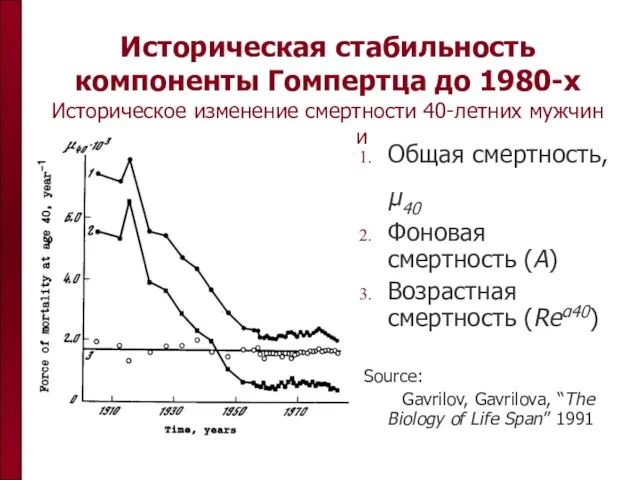
- 13. Историческая стабильность компоненты Гомпертца до 1980-х Историческое изменение смертности 40-летних мужчин Швеции Общая смертность, μ40 Фоновая
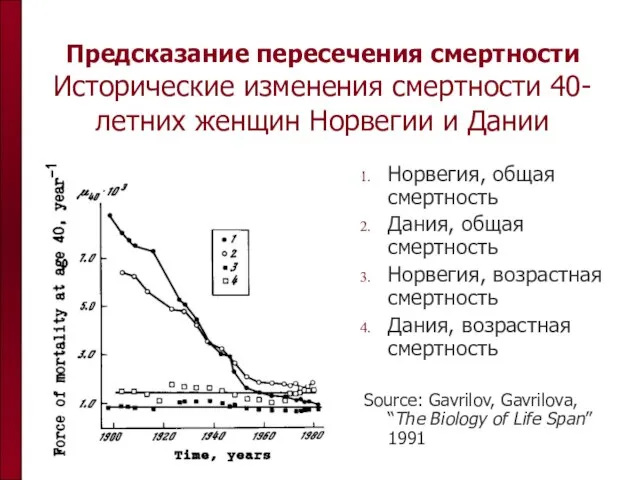
- 14. Предсказание пересечения смертности Исторические изменения смертности 40-летних женщин Норвегии и Дании Норвегия, общая смертность Дания, общая
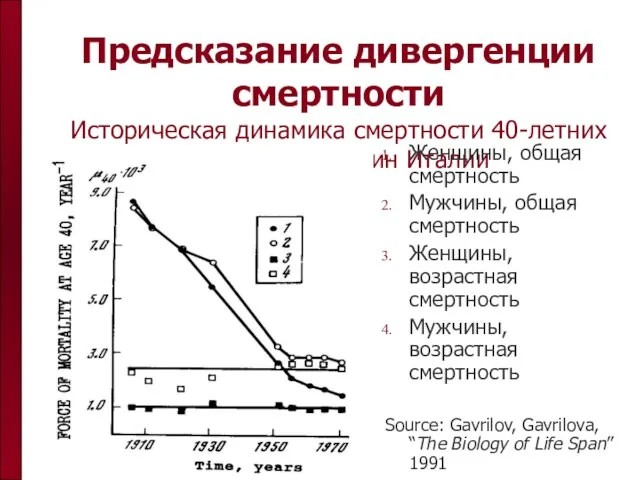
- 15. Предсказание дивергенции смертности Историческая динамика смертности 40-летних женщин и мужчин Италии Женщины, общая смертность Мужчины, общая
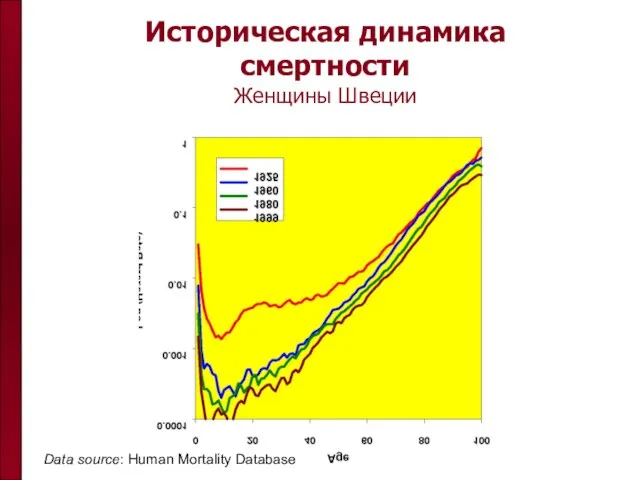
- 16. Историческая динамика смертности Женщины Швеции Data source: Human Mortality Database
- 17. Дальнейшее развитие модели Гомпертца-Мейкхема с помощью факторного анализа временных трендов смертности Интенсивность смертности (age, time) =
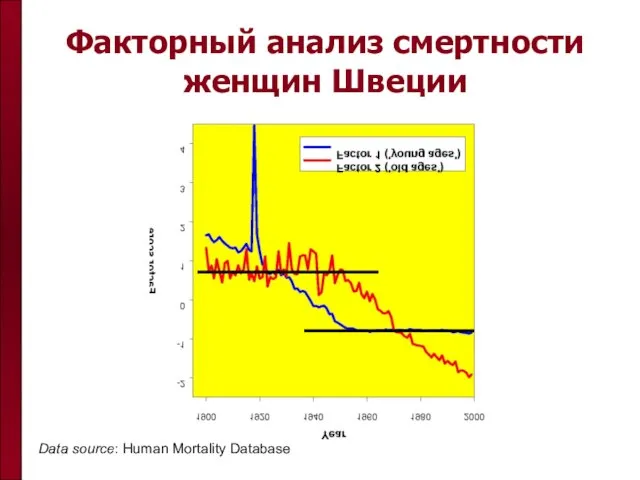
- 18. Факторный анализ смертности женщин Швеции Data source: Human Mortality Database
- 19. Следствие Тенденции смертности до 1950-х годов бесполезны и даже вредны для текущих прогнозов смертности, поскольку “правила
- 20. Предварительные выводы Определенные данные о биологических пределах смертности существовали в прошлом, но теперь эти пределы по-видимому
- 21. Компенсационный закон смертности (конвергенция смертности в старших возрастах) Относительные различия в смертности уменьшаются с возрастом поскольку
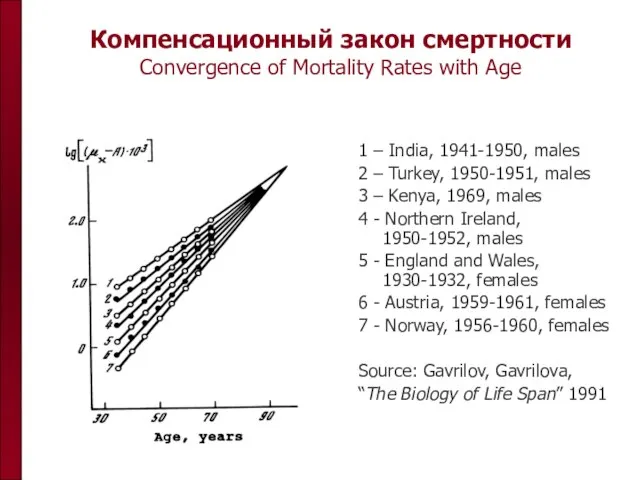
- 22. Компенсационный закон смертности Convergence of Mortality Rates with Age 1 – India, 1941-1950, males 2 –
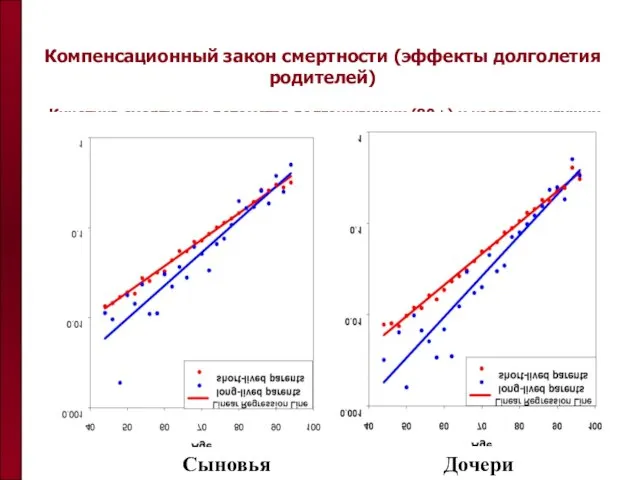
- 23. Компенсационный закон смертности (эффекты долголетия родителей) Кинетика смертности потомства долгоживущих (80+) и короткоживущих родителей Сыновья Дочери
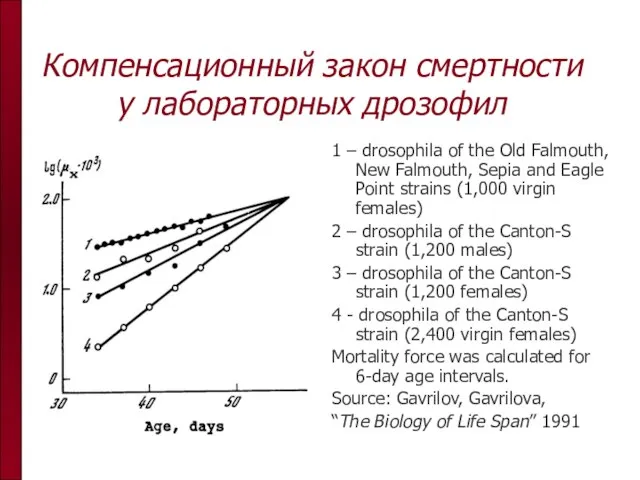
- 24. Компенсационный закон смертности у лабораторных дрозофил 1 – drosophila of the Old Falmouth, New Falmouth, Sepia
- 25. Следствия Надо быть готовым к тому, что более высокая скорость старения (актуарная) может быть связана с
- 26. Замедление роста смертности в старших возрастах (выход смертности на плато) Замедление роста смертности в старших возрастах
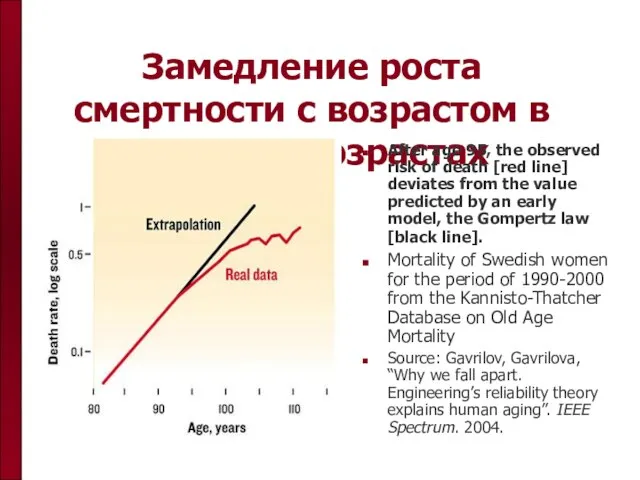
- 27. Замедление роста смертности с возрастом в старших возрастах After age 95, the observed risk of death
- 29. M. Greenwood, J. O. Irwin. BIOSTATISTICS OF SENILITY
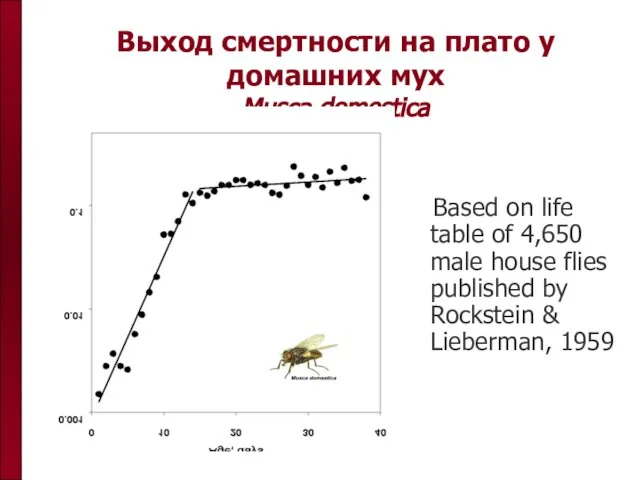
- 30. Выход смертности на плато у домашних мух Musca domestica Based on life table of 4,650 male
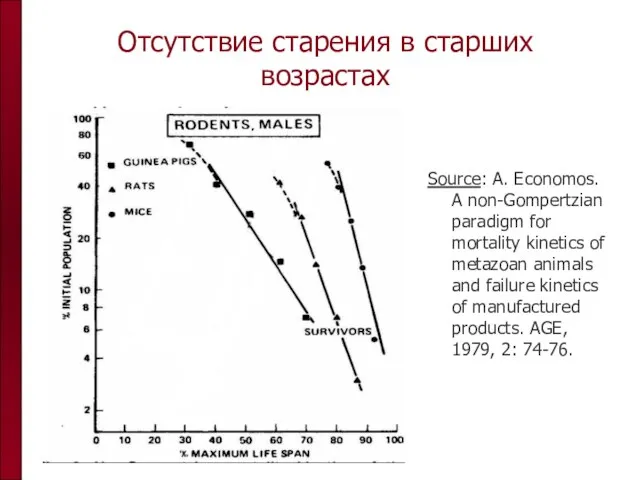
- 31. Отсутствие старения в старших возрастах Source: A. Economos. A non-Gompertzian paradigm for mortality kinetics of metazoan
- 32. Замедление роста смертности у различных видов животных Беспозвоночные: Nematodes, shrimps, bdelloid rotifers, degenerate medusae (Economos, 1979)
- 33. Существующие объяснения замедления смертности с возрастом Гетерогенность популяции (Beard, 1959; Sacher, 1966). “… sub-populations with the
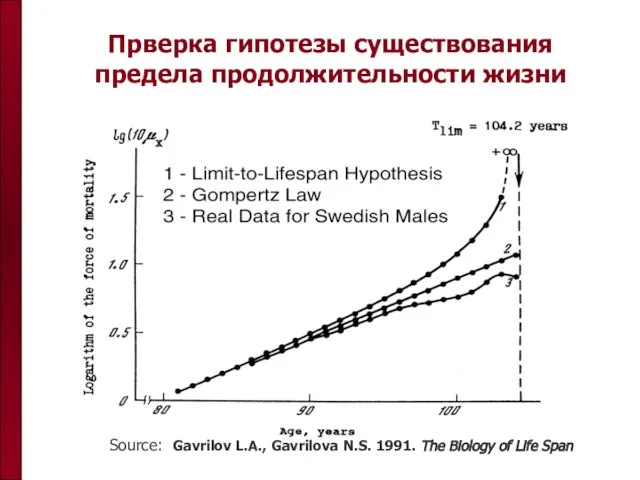
- 34. Прверка гипотезы существования предела продолжительности жизни Source: Gavrilov L.A., Gavrilova N.S. 1991. The Biology of Life
- 35. Следствия Верхнего предела индивидуальной продолжительности жизни человека не существует – нет особой фиксированной цифры, которая отделяла
- 36. Каковы объяснения существующих законов смертности Теории старения и смертности
- 37. Дополнительное эмпирическое наблюдение: Многие возрастные изменения можно объяснить кумулятивными эффектами потери клеток со временем Atherosclerotic inflammation
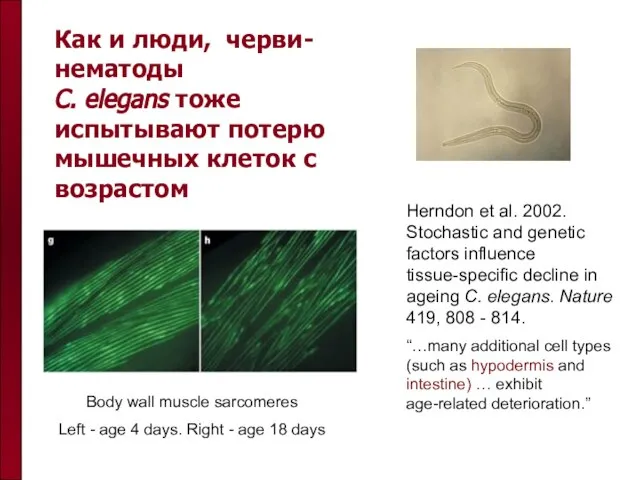
- 38. Как и люди, черви-нематоды C. elegans тоже испытывают потерю мышечных клеток с возрастом Body wall muscle
- 39. Что должна объяснять теория старения? Почему организмы большинства биологических видов, включая человека, разрушаются с возрастом? Закон
- 40. Старение – это очень общее явление!
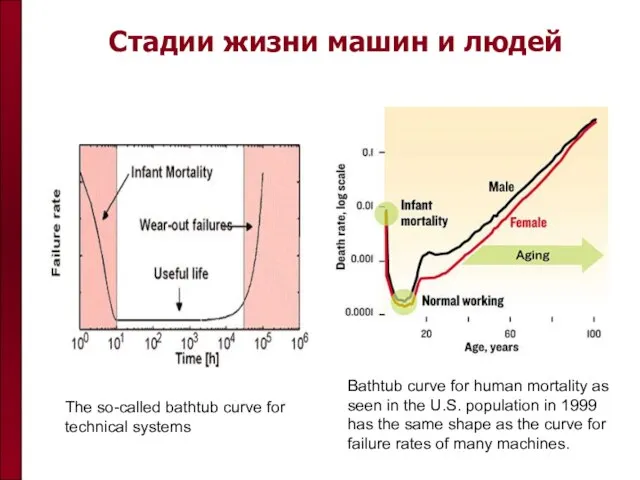
- 41. Стадии жизни машин и людей The so-called bathtub curve for technical systems Bathtub curve for human
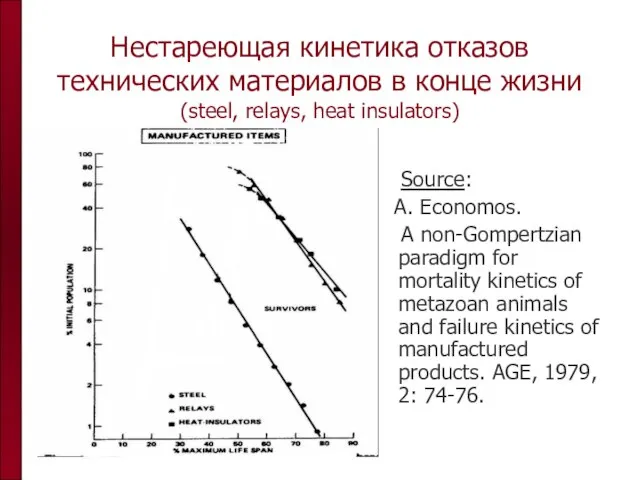
- 42. Нестареющая кинетика отказов технических материалов в конце жизни (steel, relays, heat insulators) Source: A. Economos. A
- 43. Теория надежности Теория надежности была исторически развита для описания отказов и старения сложного электронного (военного) оборудования,
- 44. Что такое теория надежности? Теория надежности – это общая теория отказов систем.
- 45. Концепция отказа системы В теории надежности отказом называется явления когда необходимая функция перестает выполняться
- 46. Определение стареющих и нестареющих систем в теории надежности Старение: растущий риск отказов с течением времени (возраста).
- 47. Стареющие и нестареющие системы Perfect clocks having an ideal marker of their increasing age (time readings)
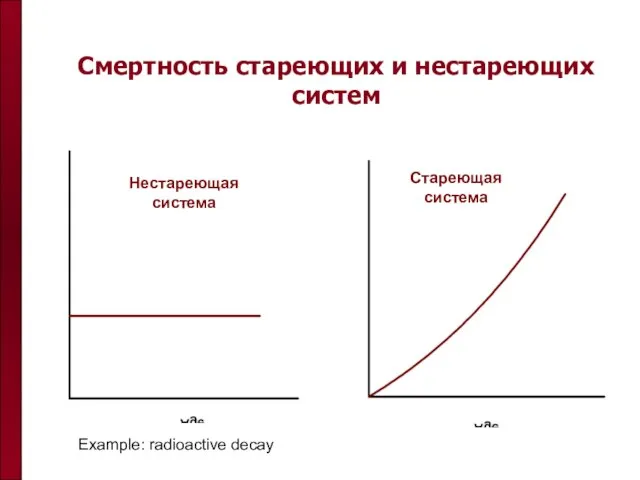
- 48. Смертность стареющих и нестареющих систем Нестареющая система Стареющая система Example: radioactive decay
- 49. Согласно теории надежности: Старение это не просто увеличение возраста Вместо этого Старение – это деградация до
- 50. Согласно теории надежности: Наступление болезни или инвалидности – это пример отказа организма Если риск таких отказов
- 51. Специфические механизмы старения могут быть различными у разных биологических видов (лосось и человек) НО Однако существуют
- 52. Концепция надежностной структуры Организация компонентов, которые важны для надежности системы, называются надежностной структурой и графически представлена
- 53. Два основных вида логической взаимосвязи Компоненты соединены последовательно Компоненты соединены параллельно Fails when the first component
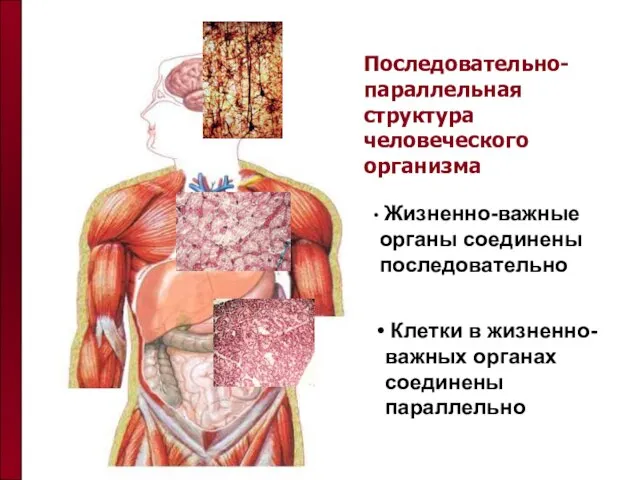
- 54. Последовательно-параллельная структура человеческого организма Жизненно-важные органы соединены последовательно Клетки в жизненно-важных органах соединены параллельно
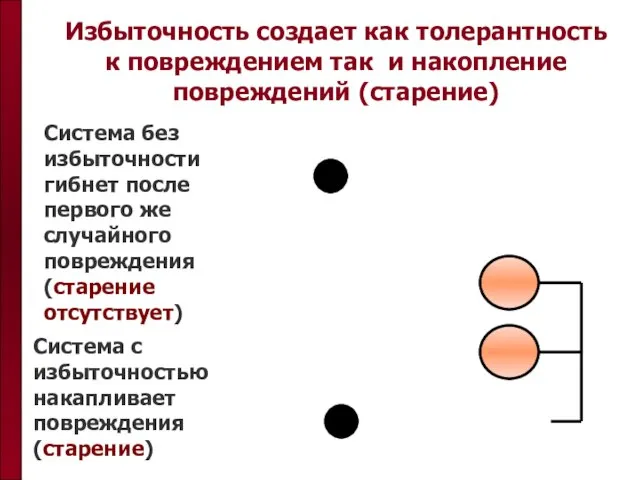
- 55. Избыточность создает как толерантность к повреждением так и накопление повреждений (старение) Система с избыточностью накапливает повреждения
- 56. Модель надежности простой параллельной системы Интенсивность отказов системы: Elements fail randomly and independently with a constant
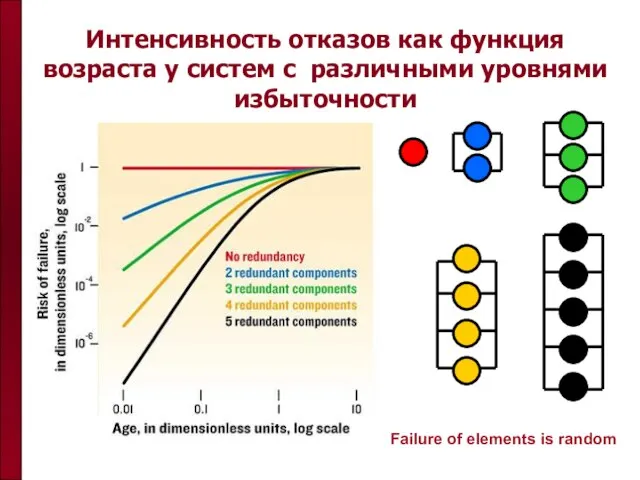
- 57. Интенсивность отказов как функция возраста у систем с различными уровнями избыточности Failure of elements is random
- 58. Стандартные модели надежности объясняют Замедление роста смертности и выход на плато в старших возрастах Компенсационный закон
- 59. Стандартные модели надежности не объясняют Закон Гомпертца для смертности биологических систем Вместо этого такие модели приводят
- 60. Догадка пришла после работы на полуразрушенной вычислительной технике в СССР The complex unpredictable behavior of this
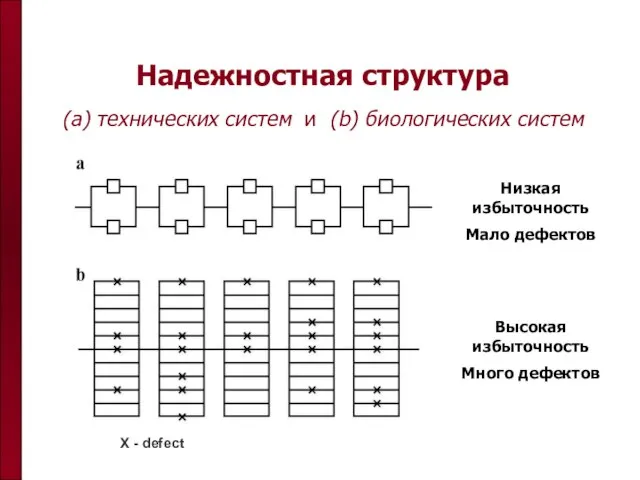
- 61. Надежностная структура (a) технических систем и (b) биологических систем Низкая избыточность Мало дефектов Высокая избыточность Много
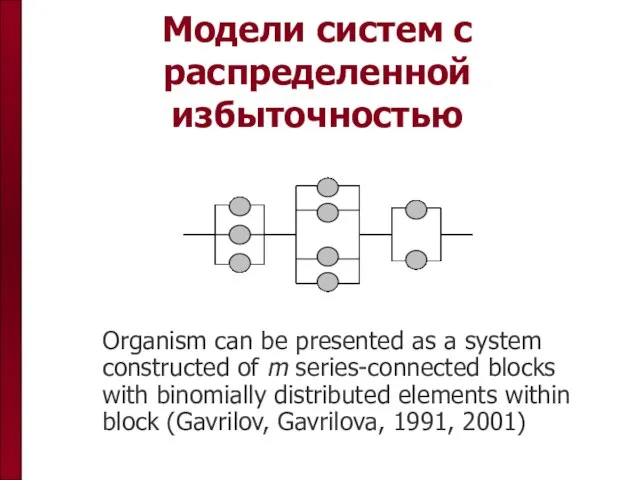
- 62. Модели систем с распределенной избыточностью Organism can be presented as a system constructed of m series-connected
- 63. Модель организма с начальным уровнем повреждений Failure rate of a system with binomially distributed redundancy (approximation
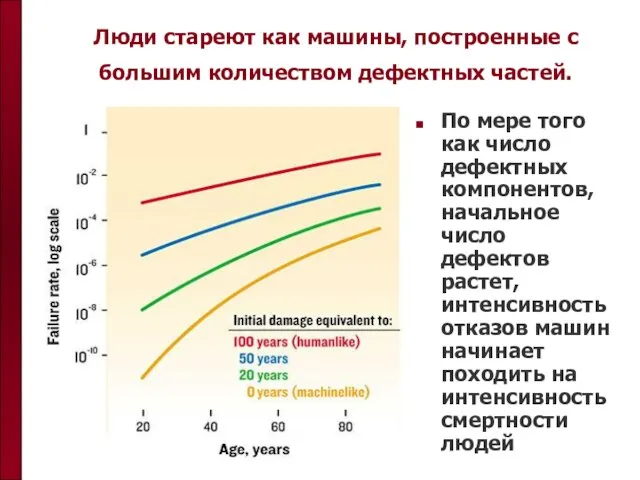
- 64. Люди стареют как машины, построенные с большим количеством дефектных частей. По мере того как число дефектных
- 65. Гипотеза начального уровня повреждений: (Idea of High Initial Damage Load ) Взрослые организмы изначально имеют высокий
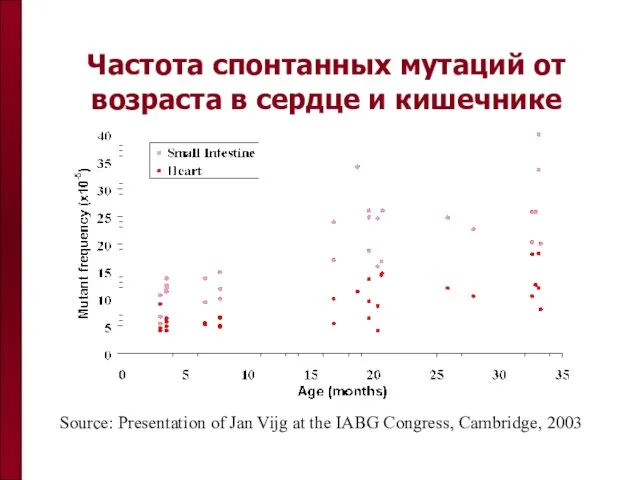
- 66. Частота спонтанных мутаций от возраста в сердце и кишечнике Source: Presentation of Jan Vijg at the
- 67. Практические следствия гипотезы начального уровня: Даже небольшой прогресс в оптимизации процессов раннего развития может потенциально привести
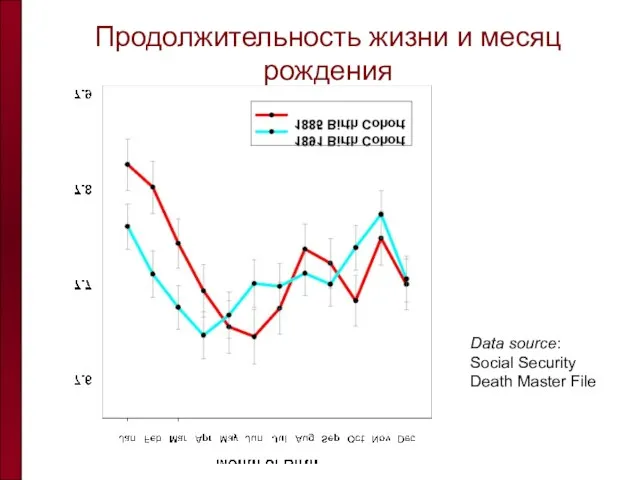
- 68. Продолжительность жизни и месяц рождения Data source: Social Security Death Master File
- 70. Благодарности This study was made possible thanks to: generous support from the National Institute on Aging,
- 71. Больше информации можно найти на сайте, посвященном продолжительности жизни человека: http://longevity-science.org
- 73. Gavrilov, L., Gavrilova, N. Reliability theory of aging and longevity. In: Handbook of the Biology of
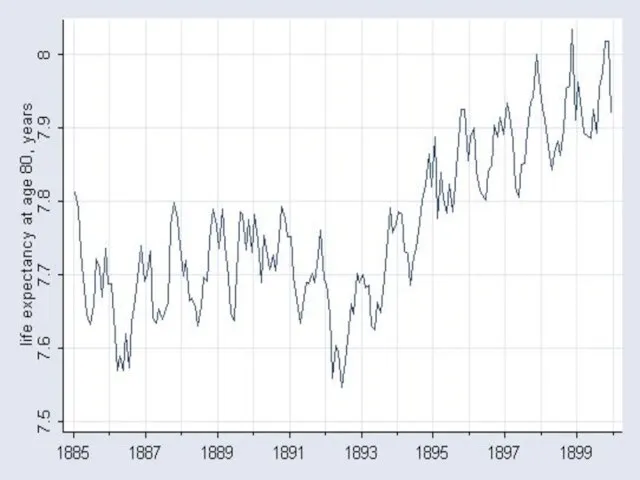
- 74. Новые результаты Является ли преувеличением закон замедления роста смертности? Исследование на основании метода угасших поколений в
- 75. Трудности оценки интенсивности смертности в старших возрастах Замедление роста смертности может быть артефактом смешения различных когорт
- 76. U.S. Social Security Administration Death Master File позволяет разрешить первые две проблемы Позволяет исследовать смертность в
- 77. What Is SSA DMF ? SSA DMF is a publicly available data resource (available at Rootsweb.com)
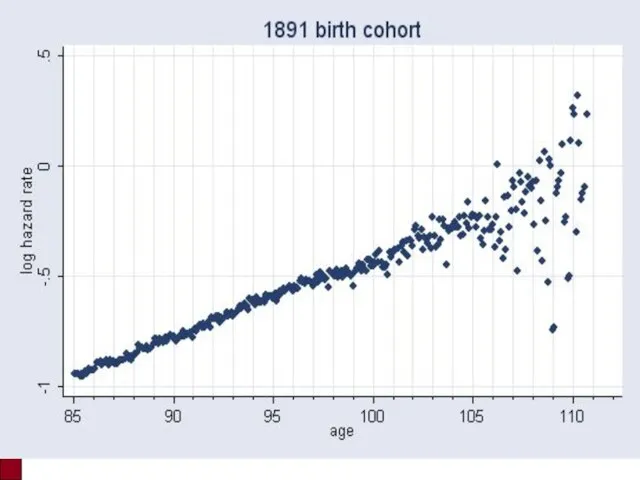
- 79. Контроль за качеством данных Исследование смертности в штатах с более совершенными данными возраста долгожителей: Records for
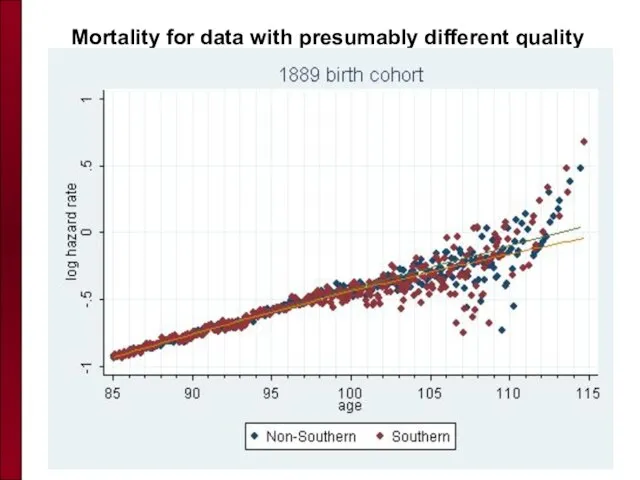
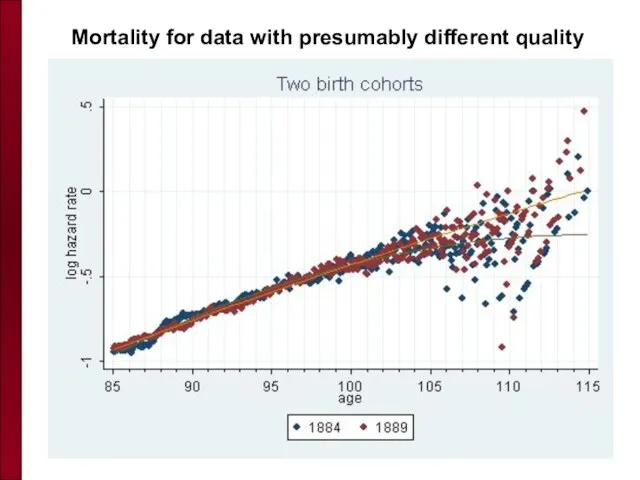
- 80. Mortality for data with presumably different quality
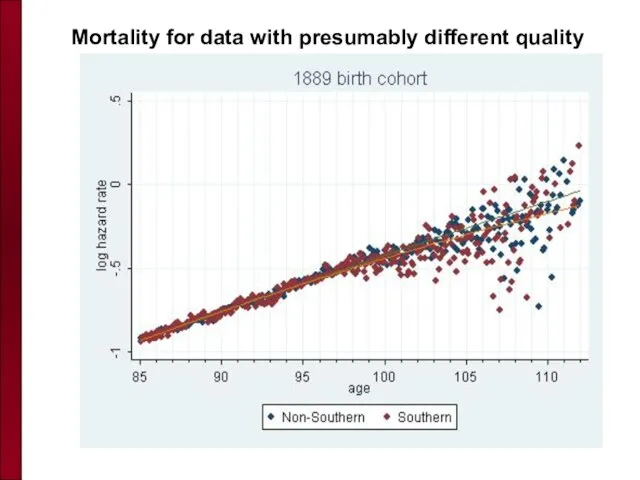
- 81. Mortality for data with presumably different quality
- 82. Mortality for data with presumably different quality
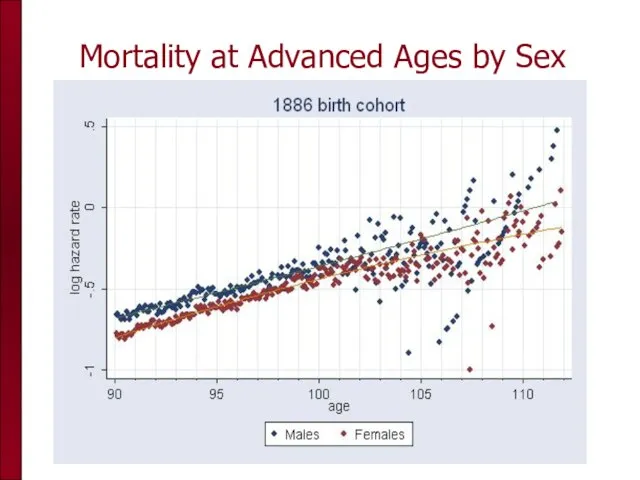
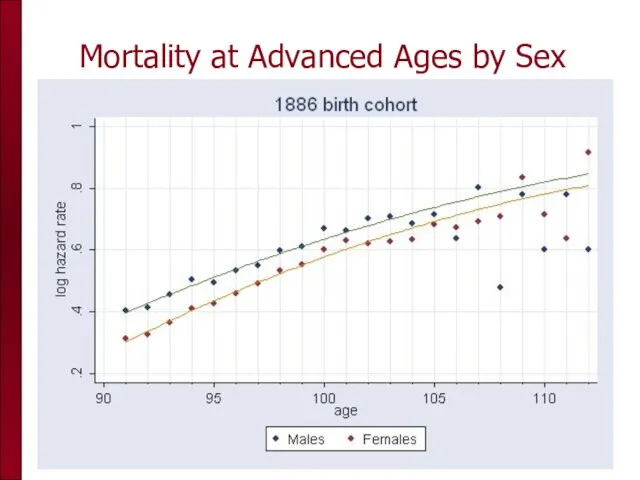
- 83. Mortality at Advanced Ages by Sex
- 84. Mortality at Advanced Ages by Sex
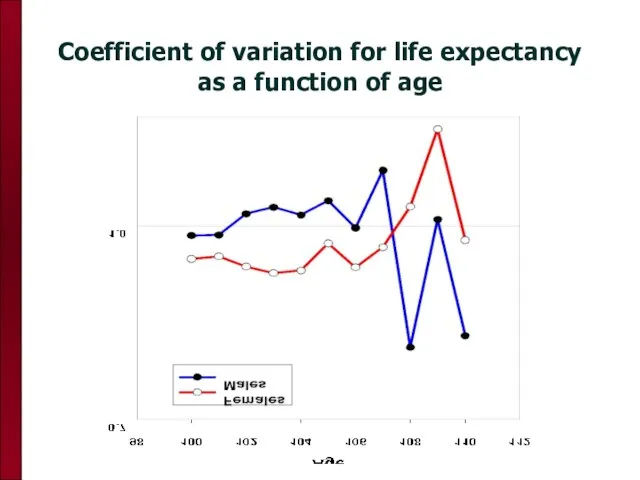
- 85. Crude Indicator of Mortality Plateau (2) Coefficient of variation for life expectancy is close to, or
- 86. Coefficient of variation for life expectancy as a function of age
- 88. Скачать презентацию

















































 Программирование
Программирование  Новогодняя маска
Новогодняя маска Автосервис. Описание продукта
Автосервис. Описание продукта 20171011_madagaskar_-
20171011_madagaskar_- Мультимедийная творческая студия «Стейджинг»
Мультимедийная творческая студия «Стейджинг» Органы цветковых растений
Органы цветковых растений Президент РФ в системе государственного управления
Президент РФ в системе государственного управления Мобильное телевидение в России и Беларуси прогнозы, мнения, опыт
Мобильное телевидение в России и Беларуси прогнозы, мнения, опыт Чернобыль… Черная быль…
Чернобыль… Черная быль… Физические законы,важные дляанестезиологаК.М. Лебединский, СПб МАПО
Физические законы,важные дляанестезиологаК.М. Лебединский, СПб МАПО Храмовое зодчество Византии
Храмовое зодчество Византии Н. М. Карамзин и Симбирск
Н. М. Карамзин и Симбирск Методические особенности развития физических качеств у хоккейного вратаря
Методические особенности развития физических качеств у хоккейного вратаря Презентация на тему возникновение искусства и религиозных верований 5 класс
Презентация на тему возникновение искусства и религиозных верований 5 класс Физика в живой природе
Физика в живой природе Биосфера: структура и функции
Биосфера: структура и функции Зарисовки предметов быта, имеющих призматическую форму с натуры и по памяти
Зарисовки предметов быта, имеющих призматическую форму с натуры и по памяти Патриотизм
Патриотизм This presentation has been IRM protected by policy
This presentation has been IRM protected by policy Правки по сайту Андрею
Правки по сайту Андрею Изучение английского языка в начальных классах. Обучение через игру.
Изучение английского языка в начальных классах. Обучение через игру. Стили общения
Стили общения Авторы проекта:
Авторы проекта: Базы данных в отечестве – могила, и наш ДМ ее себе роет
Базы данных в отечестве – могила, и наш ДМ ее себе роет Hausratversicherung
Hausratversicherung Масленица праздник
Масленица праздник Долгушева Анастасия
Долгушева Анастасия Формы бухгалтерского учета. Тема №11
Формы бухгалтерского учета. Тема №11