Моделирование исторических процессов

Введение
Моделирование – общенаучный метод исследования, который широко используется не только в естественных, но и в социально-гуманитарных науках.
Его успешно применяют экономисты, социологи, политологи, представители других общественных наук.
Этот метод доказал свою эффективность и в исторических исследованиях.

Введение
Важной проблемой математизации социального знания является определение степени универсальности математических методов и моделей, возможности переноса методов из одной области науки в другую.
В связи с этим встает вопрос о том, нужны ли специальные математические методы исследования в социально-гуманитарных науках, или достаточно тех методов, которые возникли в процессе математизации естественных наук.

Введение
Процесс математизации научного знания имеет три этапа.
Первый этап состоит в численном выражении изучаемой реальности для выявления количественной меры и границ соответствующих качеств; с этой целью проводится математико-статистическая обработка эмпирических данных, строится количественная формулировка качественно установленных фактов и обобщений.

Введение
Второй этап заключается в разработке математических моделей явлений и процессов в рассматриваемой области науки; он отражает основную форму математизации научного познания.
Третий этап – использование математического аппарата для построения и анализа конкретных научных теорий – представляет собой переход от модели к теории, формализацию основных итогов самого научного знания.

Введение
Проблемам моделирования посвящено огромное число работ, в которых вводятся десятки и сотни определений понятия "модель", классификаций моделей, типов математического моделирования.

Введение
Термином модель в философской литературе обозначают "некоторую реально существующую или мысленно представляемую систему, которая, замещая и отображая в познавательных процессах другую систему-оригинал, находится с ней в отношении сходства (подобия), благодаря чему изучение модели позволяет получить новую информацию об оригинале".

Введение
В общем плане можно выделить следующие виды моделей:
вербальные (формулирующие исследовательские гипотезы на базе наблюдений);
физические;
математические (компьютерные) модели.

Введение
Как определяется в современной науке понятие математическая модель?
Это система математических соотношений, описывающих изучаемый процесс или явление.
В общем смысле такая модель является множеством символических объектов и отношений между ними.

Введение
Как правило, до сих пор в конкретных приложениях математики чаще всего имеют дело с анализом величин и взаимосвязей между ними, которые описываются с помощью уравнений и систем уравнений.
Поэтому понятие математической модели обычно дается в следующем виде:

Введение
Математическая модель рассматривается как система уравнений, в которой конкретные величины заменяются математическими понятиями, постоянными и переменными величинами, функциями.
Обычно для этого применяются дифференциальные, интегральные и алгебраические уравнения.
Система уравнений вместе с данными, необходимыми для ее решения, называется математической моделью.

Введение
Таким образом, с практической точки зрения математическая модель, выраженная с помощью уравнений, представляет собой наиболее важный и наиболее часто используемый тип модели.

МОДЕЛИРОВАНИЕ ИСТОРИЧЕСКИХ ПРОЦЕССОВ
Специфика, уровни, типология

Специфика, уровни, типология
На сегодняшний день большинство работ, связанных с использованием математических методов в исторических исследованиях, основано на статистической обработке данных исторических источников; эти работы, в соответствии с рассмотренной периодизацией, следует отнести к первому этапу математизации научных исследований. На этом этапе удалось решить многие актуальные проблемы исторической науки, получить новое знание.

Специфика, уровни, типология
Освоив практически весь арсенал традиционных математико-статистических методов (включая дескриптивную статистику, выборочный метод, анализ временных рядов, корреляционный анализ и т.д.), отечественные исследователи во второй половине 1970‑х годов перешли к активному применению методов многомерного статистического анализа ("вершины" прикладной математической статистики).

Специфика, уровни, типология
Совершенствование методологии исторических исследований в 1980-е годы создало предпосылки для естественного перехода ко второму этапу математизации - построению математических моделей исторических процессов и явлений.

В 90-е годы в нашей стране был опубликован целый ряд работ по проблемам методологии и методики моделирования исторических процессов.
С помощью моделирования получены содержательно значимые результаты при изучении социальной мобильности в период нэпа, динамики социально-политической напряженности в России в конце XIX - начале XX вв. и т.д.
В 1996 году опубликован сборник статей "Математическое моделирование исторических процессов".

Специфика, уровни, типология
Проблематика моделирования исторических процессов и явлений обладает ярко выраженной спецификой.
Обоснование этой специфики содержится в работах И.Д. Ковальченко, в которых охарактеризованы суть и цели моделирования, предложена типология моделей исторических процессов и явлений.

Специфика, уровни, типология
Эта типология по Ковальченко включает отражательно-измерительные и имитационные (имитационно-прогностические) модели.
Имитационно-прогностические модели, в свою очередь, делятся на имитационно-контрфактические и имитационно-альтернативные модели исторических процессов. К середине 1990-х гг. контрфактическое моделирование было отмечено Нобелевской премией, которую получили известные американские клиометристы Р.Фогель и Д.Норт.

Специфика, уровни, типология
Измерительное моделирование основано, как правило, на выявлении и анализе статистических взаимосвязей в системе показателей, характеризующих изучаемый объект.
Здесь речь идет о проверке содержательной модели с помощью методов математической статистики. Роль математики сводится в этом случае к статистической обработке эмпирического материала.

Специфика, уровни, типология
В современной классификации математических моделей в исторических исследованиях такие модели относятся к классу статистических.

Специфика, уровни, типология
Гораздо менее апробированными в практике отечественных исследований являются математические модели, применение которых не ограничивается обработкой данных источника.
Модели такого типа в современной классификации относятся к классам имитационных и аналитических моделей.

Специфика, уровни, типология
Целью таких моделей может быть:
реконструкция отсутствующих данных о динамике изучаемого процесса на некотором интервале времени;
анализ альтернатив исторического развития;
теоретическое исследование возможного поведения изучаемого явления (или класса явлений) по построенной математической модели.

Специфика, уровни, типология
Аналитические и имитационные модели относятся к моделям дедуктивного типа в отличие от статистических (измерительно-отражательных) моделей, при построении которых преобладает индуктивный подход.
Математические модели дедуктивного типа позволяют выводить новое знание путем анализа построенной модели как математического объекта.

Специфика, уровни, типология
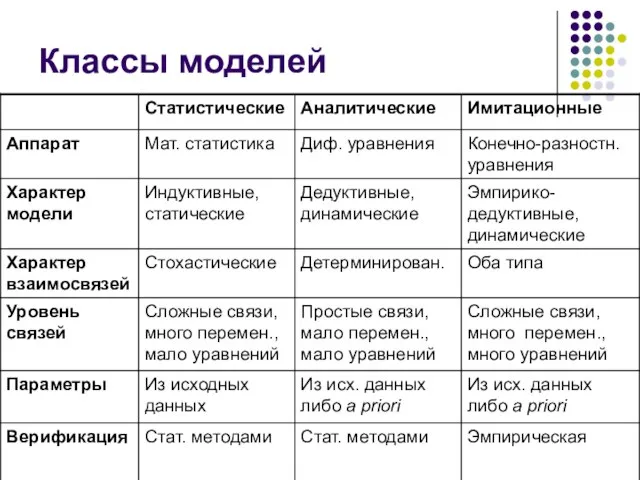
Таким образом, к началу XXI века сформировались три класса математических моделей исторических процессов, которые мы и рассматриваем в нашем курсе:
статистические,
имитационные,
аналитические

МОДЕЛИРОВАНИЕ ИСТОРИЧЕСКИХ ПРОЦЕССОВ
Статистические модели

Статистические модели
Как правило, в статистических моделях используются методы математической статистики: это регрессионные модели (модели множественной регрессии) и модели факторного анализа.

Статистические модели
Основная цель статистических моделей – выявление и отбор факторов, влияющих на результат.
Критерий верификации – процент объясненной дисперсии.
Индуктивный характер модели; дедукции из модели являются тривиальными.

Статистические модели
Характер взаимосвязей: стохастический (статистический), т.е. недетерминированный.
Требования к данным достаточно высоки: модели строятся из предположений о роли факторов, с привлечением большого количества статистических данных высокого качества.
Параметры модели выводятся из исходных данных с помощью статистических методов.

Статистические модели
Основные предположения для построения модели могут быть очень сложными для выполнения и проверки (например, линейный характер связей).
Ограничения:
малое число уравнений;
большое число переменных, сложные связи между ними;
обратные связи трудны для исследования;
весьма ограниченные формы динамических связей.

МОДЕЛИРОВАНИЕ ИСТОРИЧЕСКИХ ПРОЦЕССОВ
Аналитические модели

Аналитические модели
В аналитических моделях используется математический аппарат дифференциальных уравнений и марковских цепей. Результаты получаются путем решения систем уравнений либо аналитически (в общем виде), либо численно (с помощью компьютера).

Аналитические модели
Основная цель – анализ динамики на основе теоретических предположений о связях между переменными.
Применение пока весьма ограничено. Верификация модели возможна только статистическими методами.
Дедуктивный характер модели: модели выводятся из теории.

Аналитические модели
Характер взаимосвязей: детерминированный (т.е. не статистический).
Требования к данным: для верификации и подтверждения надежности модели можно использовать данные разного качества.
Параметры модели либо задаются a priori, либо выводятся из исходных данных с помощью статистических методов.

Аналитические модели
Основные предположения для построения модели строятся на упрощенном представлении о переменных и связях между ними.
Ограничения:
малое число уравнений;
малое число переменных;
обратные связи трудны для исследования;
простые формы динамических связей.

МОДЕЛИРОВАНИЕ ИСТОРИЧЕСКИХ ПРОЦЕССОВ
Имитационные модели

Имитационные модели
В имитационных моделях используется математический аппарат конечно-разностных уравнений.
Моделирующий алгоритм позволяет по исходным данным, содержащим сведения о начальном состоянии процесса (входной информации) и его параметрах, получить сведения о состояниях процесса на каждом последующем шаге.

Имитационные модели
Основная цель – анализ динамических процессов с не поддающимися аналитическому изучению сложными связями между переменными. Допускаются нелинейные и обратные связи.
Верификация модели: эмпирически можно проводить сильные тесты модели.
Тенденция к построению сложных эмпирико-дедуктивных теорий (модели отчасти выводятся из теории).

Имитационные модели
Характер взаимосвязей: предполагаются как детерминистические, так и стохастические связи.
Требования к данным: возможны данные низкого качества для подтверждения надежности модели. Ошибкам измерения особого внимания не уделяется.
Параметры модели либо задаются a priori, либо выводятся из исходных данных с помощью статистических методов.

Имитационные модели
Основные предположения: приближенно воспроизводится сам изучаемый процесс, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени.
Ограничения:
большое число переменных и уравнений;
сложные связи между ними;
однако полученное решение всегда носит частный характер, отвечая фиксированным значениям параметров системы, входной информации и начальных условий.

Классы моделей

Примеры применения моделей в истории
Примером заимствования моделей, разработанных в естественных науках, могут служить модели роста численности популяции. Простейшая модель такого рода (закон экспоненциального роста) была использована в XIX веке Т. Мальтусом.
Однако эта модель не учитывала, что общий объем жизненных ресурсов накладывает естественные ограничения на динамику развития процесса.

Примеры применения моделей в истории
С учетом таких ограничений процессы роста описываются т.н. логистической моделью. Логистическая модель роста народонаселения была предложена П. Ферхюльстом (в этой модели предполагается, что прирост численности в каждый момент прямо пропорционален достигнутой численности и обратно пропорционален ее квадрату).

Примеры применения моделей в истории
Другими примерами математического моделирования для изучения сложных социальных систем могут служить:
применение модели клеточных автоматов (для изучения электорального поведения);
теоретико-игровые модели (для изучения конфликтов, например, Карибского кризиса 1962 г.) и др.

Примеры применения моделей в истории
Важно, что модели позволяют не только углубить понимание сложных, развивающихся систем, но и прогнозировать их развитие, например:
модель Форрестера, имитирующая развитие американской экономики и демонстрирующая наличие коротких и длинных циклов (развитие этой модели касалось уже глобальных процессов);
известная модель Н. Моисеева для анализа последствий ядерной войны (эффект "ядерной зимы").

Примеры применения моделей в истории
Целая серия математических моделей аналитического типа была предложена в работах Ю. Бокарева. Одна из них посвящена анализу функционирования экономики СССР в 20-е годы в предположении, что в конце 1920 г. денежное обращение было бы полностью заменено натуральным обменом.

Примеры применения моделей в истории
Если обменивается вся продукция, экономическая система испытывает колебания вокруг положения равновесия с периодом около 10 лет.
Если обменивается только часть продукции, то после короткого периода роста производства начинается снижение, а затем объемы продукции стабилизируются, совершая едва заметные колебания вокруг уровней равновесия (модель застойной экономики).

Примеры применения моделей в истории
Интересные результаты были получены Л.И.Бородкиным и М.В.Свищевым при изучении социальной мобильности в период нэпа, процессов дифференциации доколхозного крестьянства. Было показано, что эти процессы не вели к социальной «поляризации» деревни. При сохранении тенденций середины 20-х гг. доля середняков постепенно увеличивалась бы, стабилизируясь в первой половине 1930-х гг.

МОДЕЛИРОВАНИЕ ИСТОРИЧЕСКИХ ПРОЦЕССОВ
Конечно-разностные и дифференциальные уравнения

Конечно-разностные и дифференциальные уравнения
Построение модели, изучение ее поведения во времени, оценка роли различных факторов наиболее эффективно осуществляются с помощью формальных методов, в первую очередь, разностных или дифференциальных уравнений.
Такая формализация позволяет перейти от словесного описания концептуальной модели к ее математической форме.

Конечно-разностные и дифференциальные уравнения
При этом важно понимать принципы построения (уметь "читать") эти уравнения, а решение их можно доверить компьютерным программам, которые позволят "увидеть" построенную модель и проследить ее изменение во времени.
Разумеется, при интерпретации полученных решений необходимо снова вернуться к языку содержательных понятий.

Конечно-разностные и дифференциальные уравнения
Разностные уравнения применяются, когда состояние исследуемого процесса фиксируется в определенные дискретные моменты времени. Интервал времени при этом предполагается постоянным (часто это связано с данными официальной статистики).
Если же интервал становится бесконечно малым, то процесс рассматривается как непрерывный и изучается с помощью дифференциальных уравнений.

Конечно-разностные и дифференциальные уравнения
В общем случае дифференциальными называются уравнения, связывающие между собой независимую переменную x, искомую функцию y и ее производные различных порядков по x. Часто роль независимой переменной играет время t.
В отличие от разностного уравнения дифференциальное описывает динамику процесса в каждый момент времени t.

Конечно-разностные и дифференциальные уравнения
Простейшим дифференциальным уравнением является уравнение y' = f(x).
Любая функция , которая, будучи подставлена в дифференциальное уравнение, обращает его в тождество, называется решением этого уравнения.

Конечно-разностные и дифференциальные уравнения
Общим решением простейшего дифференциального уравнения является неопределенный интеграл:
y = ∫f(x)dx + C (где С – произвольная константа).
Значение константы С определяется начальными условиями и позволяет получить частное решение уравнения из бесконечного множества возможных решений.

Конечно-разностные и дифференциальные уравнения
Общего метода интегрирования дифференциальных уравнений (даже первого порядка) не существует, и только для некоторых типов уравнений можно указать способы их аналитического решения.
Поэтому чаще всего дифференциальные уравнения решают численными методами, в частности, заменяя их разностными уравнениями.

МОДЕЛИРОВАНИЕ ИСТОРИЧЕСКИХ ПРОЦЕССОВ
Конечно-разностные уравнения. Примеры моделей

Конечно-разностные уравнения
Простейшее разностное уравнение можно получить в модели динамики численности популяции.
Обозначим через Ni численность населения в момент времени i.
Если нет ограничений со стороны внешней среды и миграция отсутствует, то в следующий момент времени (i+1), например, в следующем году, к численности населения надо добавить число родившихся и вычесть число умерших.

Конечно-разностные уравнения
Величина прироста за счет рождаемости задается выражением rN, где r – коэффициент рождаемости.
Величина убыль за счет смертности задается выражением mN, где m – коэффициент смертности.
Таким образом, в момент времени (i+1) численность населения Ni+1 станет равной Ni + r*Ni – m*Ni

Конечно-разностные уравнения
Таким образом, мы получили простейшее конечно-разностное уравнение динамики численности населения:
Ni+1=Ni + rNi – mNi
или
Ni+1=Ni + (r – m)Ni
где разность (r – m) – коэффициент прироста.
Если этот коэффициент больше нуля (рождаемость выше смертности), население растет, если меньше нуля – убывает.

Примеры моделей
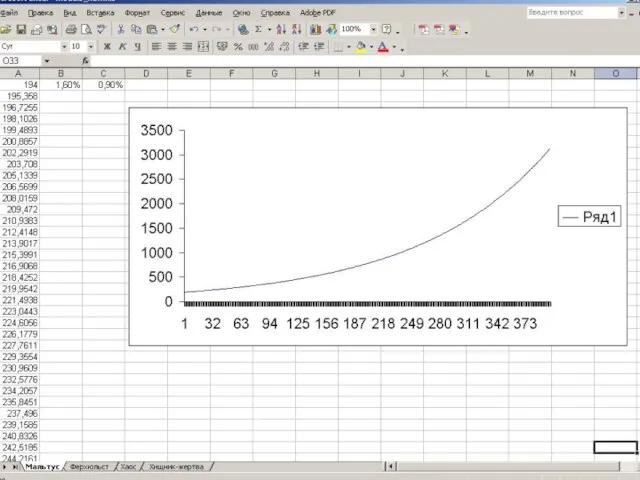
Эта модель роста численности населения была предложена Т. Мальтусом. Она описывала неограниченный, экспоненциальный рост человечества.
В результате был получен весьма неблагоприятный прогноз, связанный с невозможностью обеспечить жизненными ресурсами неограниченно растущее население.

Примеры моделей
Однако, экспоненциальный рост не может продолжаться долго. Естественные ограничения на него накладывает внешняя среда, ресурсы которой не безграничны.
В простейшем случае можно предположить, что коэффициент прироста не является постоянным, а убывает с течением времени, по мере роста населения.

Примеры моделей
К этому можно прийти в результате следующего рассуждения: изменение численности населения за некоторый промежуток времени складывается из прироста, обусловленного рождаемостью, т.е. rN (r – коэффициент рождаемости), убыли, обусловленной смертностью, т.е. –mN (m – коэффициент смертности), а также дополнительной убыли, пропорциональной квадрату численности населения (–bN2).

Примеры моделей
Эта дополнительная убыль связана с повышением вероятности заболеваний и другими проявлениями "сопротивления среды".
В результате получается модель, которая была предложена П. Ферхюльстом:
Ni+1 = Ni +rNi – mNi – bNi2
Решение этого уравнения приводит к тому, что численность населения не растет неограниченно, а стремится к некоторой предельной величине.

Примеры моделей
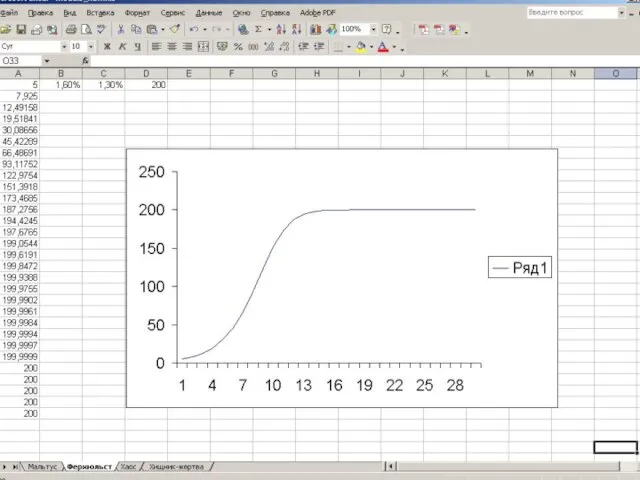
График этого уравнения называется логистической кривой
Вблизи начальной точки его вид напоминает кривую экспоненциального роста, затем, после точки перегиба, кривая все ближе подходит к прямой, соответствующей предельной численности населения.

Примеры моделей
Таким образом, система в данном случае имеет устойчивое (стационарное) состояние; этому состоянию соответствует прирост населения, равный нулю (рождаемость уравновешивается смертностью).

Примеры моделей
Если динамических переменных больше одной, тогда и уравнений (дифференциальных или разностных) должно быть несколько, т.е. это система уравнений.
В качестве примера системы двух уравнений укажем известную модель Лотки-Вольтерра (в биологии известна как модель "хищник-жертва", в политологии – как модель "народ-правительство", в истории – как модель "бароны и крестьяне").

Примеры моделей
Пусть сосуществуют два вида, две группы, две силы. Их численности или их влияния зависят друг от друга.
Так, если количество "жертв" меньше нормы, "хищники" начинают вымирать, причем тем быстрее, чем меньше "жертв". Если же количество "жертв" больше определенного порога, число "хищников" начинает возрастать, опять-таки тем быстрее, чем больше "жертв".

Примеры моделей
С другой стороны, если число "хищников" меньше определенной нормы, число "жертв" начинает расти и тем быстрее, чем меньше "хищников"; а если число "хищников" превышает норму, число "жертв" начинает уменьшаться, причем тем быстрее, чем больше "хищников".

Примеры моделей
Эти возможности оказались довольно перспективными для использования модели при изучении социальной динамики.
Большую известность приобрели работы немецкого ученого В. Вайдлиха. Он разработал систему моделей изучения динамики социально-экономических и политических факторов (производство и потребление товаров, инвестиции и т.п.)

Примеры моделей
Модель Лотки-Вольтерра была использована В.Вайдлихом для изучения отношений между "народом" и "правительством" (или, например, парламентом и правительством). Одной переменной в этой модели является степень силы правительства, а другой переменной – степень политического влияния народа (парламента).

Примеры моделей
Если использовать эту модель как модель отношений "хищник-жертва", когда правительство проводит репрессивную политику, которую поддерживает народ, то, как это и должно следовать из свойств модели, политическая ситуация испытывает циклические изменения – колебания около положения равновесия.

Примеры моделей
При наличии взаимного "сотрудничества" (кооперативного поведения) сильное правительство поддерживает демократические институты общества, слабое стремится ограничить их влияние. И наоборот: если влияние народа велико, он поддерживает деятельность правительства; если невелико – политика правительства встречает противодействие.

Примеры моделей
В этом случае система имеет два состояния равновесия: сильную демократию с сильным правительством и значительной ролью народа или противоборствующую демократию со слабым правительством и столь же слабым общественным влиянием.

Примеры моделей
Наконец, при наличии конкуренции (антагонистического поведения) правительства и народа сильное правительство стремится подавить демократические институты, а слабое правительство поддерживает их рост; с другой стороны, значительное влияние народа приводит к уменьшению роли правительства, а при слабом влиянии народа требуется сильное правительство.

Примеры моделей
Здесь тоже имеет два состояния равновесия: это либо диктатура с сильным правительством и слабым народом, либо анархия, при которой народ саботирует решения слабого правительства.

Примеры моделей
Таким образом, важнейшими характеристиками динамики системы являются положения равновесия и предельные циклы. Они называются аттракторами (притягивающими множествами).

Примеры моделей
Если менять параметры структурно-устойчивой системы, то ее поведение также будет меняться, но его качественные параметры будут достаточно устойчивы.
Однако при достижении критических величин параметров системы в ней происходит бифуркация – поведение системы качественно меняется, она переходит на новую траекторию.

Примеры моделей
Например, при прохождении точки бифуркации из состояния равновесия может возникнуть колебательный периодический режим.
Когда же система попадает в хаотический режим, ее поведение становится апериодическим и кажется случайным, подверженным непредсказуемым внешним воздействиям.

Примеры моделей
На самом деле это поведение не является случайным, оно определено законом функционирования системы, но прогнозировать поведение системы в хаотическом состоянии невозможно.
Изучением закономерностей поведения сложных систем занимается новое быстро развивающееся междисциплинарное направление – синергетика (или теория самоорганизации).

СИНЕРГЕТИКА
Синергетика возникла в 1970-х гг. Ее развитие связывают с именами таких известных ученых как И. Пригожин (лауреат Нобелевской премии), Г. Хакен, С.П. Курдюмов и др. Математический аппарат синергетики разработан в рамках теории нелинейных дифференциальных уравнений (в этой связи часто используют термины «теория катастроф», «теория хаоса»).
Синергетика изучает динамику развития неустойчивых ситуаций, в которых малые (нередко – случайные) воздействия могут вызвать большие последствия. Процесс в результате может выйти на новую траекторию, устремиться к новому аттрактору.