Начертательная геометрия (лекции)

Начертательная геометрия – это наука о способах
отображения пространственных форм
на плоскости.
Предметом начертательной геометрии являются пространственные формы и их соотношения.
Изображения объектов трехмерного пространства
на плоскости получают методом проецирования.
Поэтому проекционный метод построения изображений является основным методом НГ.
Проецирование – это получение изображения объекта с помощью проецирующих лучей на плоскость.

Виды проецирования и их свойства
Аппарат проецирования включает в себя проецирующие лучи (проецирующие прямые), проецируемый объект и плоскость, на которой получается изображение (плоскость проекций).
В зависимости от положения центра проецирования и
направления проецирующих прямых по отношению
к плоскости проекций, проецирование может быть:
центральным,
параллельным
прямоугольным (ортогональным).

Центральное проецирование
S – центр проецирования
П1 – плоскость проекций
l, l’,… - проецирующие прямые
А, В, С – точки пространства
l ⊃S
l ⊂ A,B,C
l ∩П1 = А1, В1, С1
l ⊃S
l ⊂ A,B,C
l ∩П1 = А1, В1, С1
Свойства центрального проецирования
Проекцией точки является точка
Проекцией прямой линии является прямая
Проекцией точки, лежащей на прямой является
точка, лежащая на проекции
данной прямой. Если С ⊂ АВ, то C1 ⊂ А1В1.
Точка пересечения линий проецируется в точку пересечения их проекций.
S – центр проецирования
П1 – плоскость проекций
А, В, C, E, D– точки пространства

Параллельное проецирование
i, j ‖ s
α°– угол между проецирующими прямыми и плоскостью проекций α°- не равно 90°
i, j ⊃ A, B. A1. B1 = I, j ∩ П1
А1, В1 - параллельные проекции точек

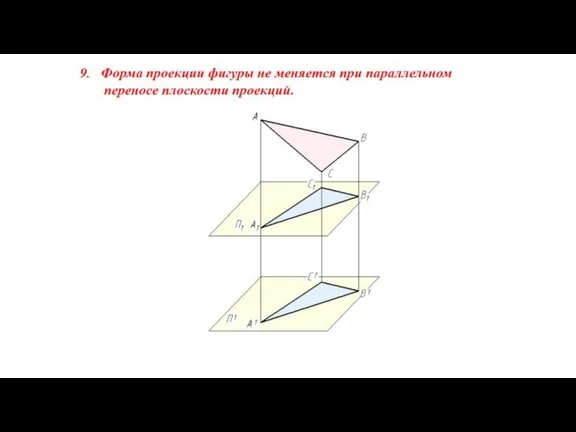
Свойства параллельного проецирования
1-3 справедливы и для
параллельного проецирования
4. Проекциями параллельных
прямых являются параллельные прямые.
Если MN ll DE, то М1 N1llD1E1
5. Отношение отрезков параллельных прямых равно отношению
проекций этих отрезков.
Если MN II DE, то MN/DE = M1N1/D1E1 (MD/DN=M1D1/D1N1)
6. Прямая параллельная плоскости проекций проецируется в
натуральную величину.
Если MN II П1, то MN= M1N1

Прямоугольное (ортогональное) проецирование
α° - равно 90° (Проецирующие прямые перпендикулярны
плоскости проекций)
Свойства прямоугольного проецирования
1 – 6 справедливы

Длина проекции отрезка прямой равна длине самого отрезка,
умноженной на косинус угла наклона прямой к плоскости проекций.
0 ˂ А1 В1 ˂ АВ
АВ = А1 В1 * cos α
МВ‖А1В1
МВ=А1В1
АМ⊥ВМ
AM=AA1-A1M
АВ – натуральная величина
отрезка

Теорема о проецировании прямого угла
Если хотя бы одна из сторон прямого угла параллельна одной из плоскостей проекций, а другая ей не перпендикулярна,
то прямой угол на эту плоскость проецируется без искажения.
a⊥b, a‖П1
Если a‖П1, то a1⊥b1

Прямая задача –
построение проекций по пространственной модели;
Обратная задача – по проекциям воссоздание
пространственной модели
Прямая и обратная задачи
К чертежу предъявляются следующие требования: обратимость, точность, простота, наглядность.

Комплексные чертежи «Точка, прямая, плоскость»
Комплексным называется чертеж, состоящий из совокупности взаимосвязанных ортогональных проекций.

П2 – фронтальная плоскость проекций
П1 – горизонтальная плоскость проекций
Х12 – ось проекций
П2⊥П1
АА2=А1А12 расстояние до фронтальной плоскости
АА1 = А2А12 расстояние до горизонтальной плоскости
А2А1 – линия связи
А2А1 ⊥ Х12
Две проекции точки определяют ее положение в пространстве
Комплексный чертеж точки

Комплексный чертеж прямой
Прямые, непараллельные и неперпендикулярные плоскости проекций называются прямыми общего положения.
Прямая на комплексном чертеже может быть задана:
двумя точками (А, В);
своими проекциями (m1, m2).

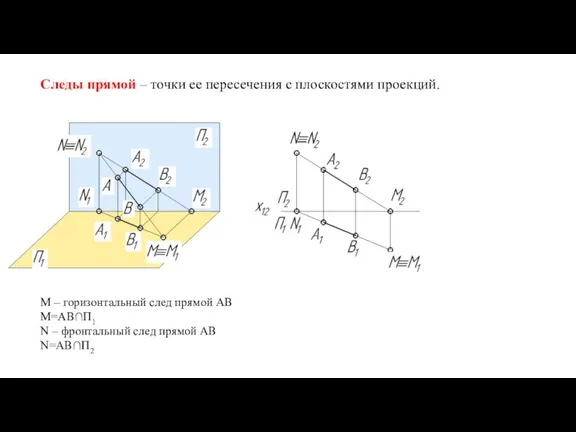
Следы прямой – точки ее пересечения с плоскостями проекций.
М – горизонтальный след прямой AB
М=AB∩П1
N – фронтальный след прямой AB
N=AB∩П2

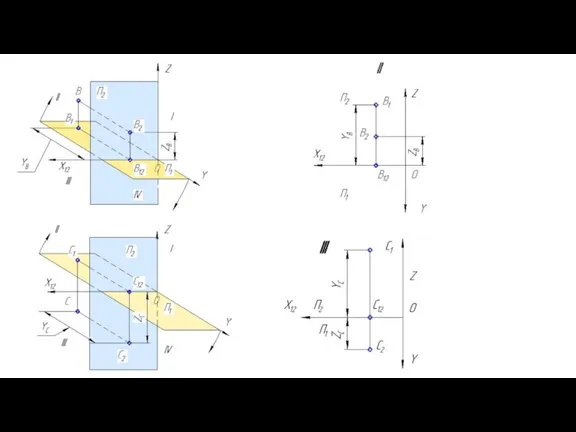
Прямые частного положения (прямые уровня и проецирующие)
Прямые частного положения – это прямые параллельные и перпендикулярные плоскостям проекций.
Прямые уровня
Прямые уровня – прямые параллельные плоскостям проекций.
Различают три линии уровня:
1) прямую, параллельную горизонтальной плоскости проекций; называют горизонтальной или горизонталью h;
2) прямую, параллельную фронтальной плоскости проекций; называют фронтальной или фронталью f;
3) прямую, параллельную профильной плоскости проекций; называют профильной р.
Каждая линия уровня будет проецироваться в натуральную величину
на ту плоскость проекций, которой она параллельна, углы наклона, которые эта прямая образует с двумя другими плоскостями проекций, также будут проецироваться на эту плоскость без искажения.

Горизонталь
h2 II X12 ; h1 – натуральная величина;
α °- угол наклона прямой к фронтальной плоскости проекций.

Фронталь
f1 II X12 ; f2 - натуральная величина;
β ° - угол наклона прямой к горизонтальной плоскости проекций.

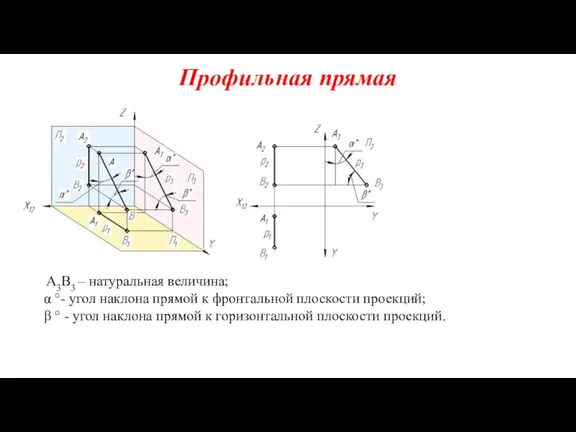
Профильная прямая
А3В3 – натуральная величина;
α °- угол наклона прямой к фронтальной плоскости проекций;
β ° - угол наклона прямой к горизонтальной плоскости проекций.

Проецирующие прямые

Взаимное расположение прямых