Теорема о сумме углов треугольника

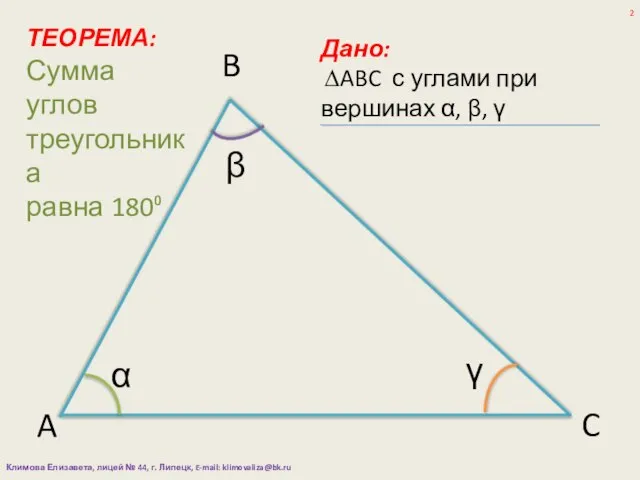
α
β
γ
A
B
C
Дано:
∆ABC с углами при вершинах α, β, γ
ТЕОРЕМА:
Сумма углов треугольника
равна 180⁰
Климова Елизавета, лицей № 44, г. Липецк, E-mail: [e-mail]

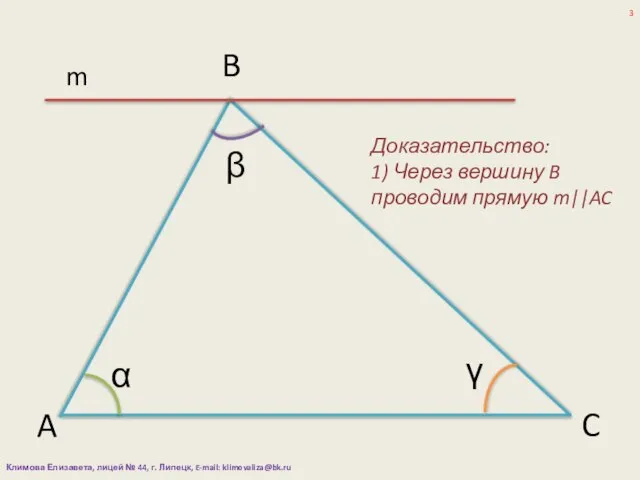
α
β
γ
A
B
C
Доказательство:
1) Через вершину B проводим прямую m||AC
m
Климова Елизавета, лицей № 44, г. Липецк, E-mail: [e-mail]

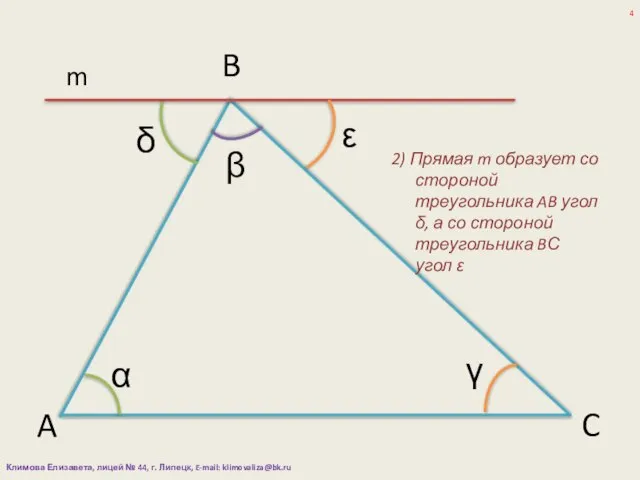
α
β
γ
A
B
C
m
2) Прямая m образует со стороной треугольника AB угол δ, а со стороной треугольника BС угол ε
δ
ε
Климова Елизавета, лицей № 44, г. Липецк, E-mail: [e-mail]

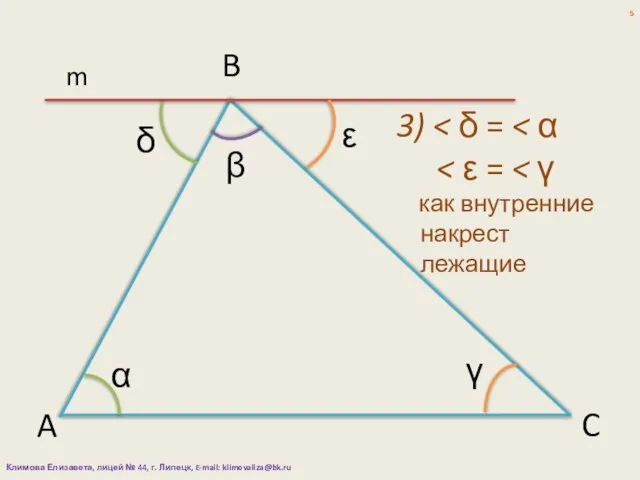
α
β
γ
A
B
C
m
3) < δ = < α
< ε = < γ
как внутренние накрест лежащие
δ
ε
Климова Елизавета, лицей № 44, г. Липецк, E-mail: [e-mail]

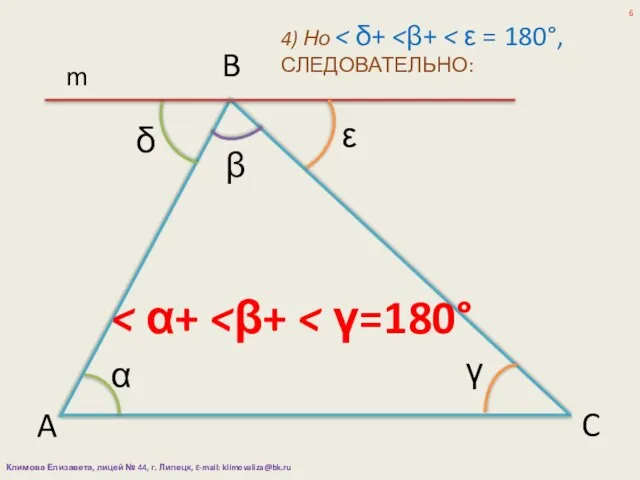
α
β
γ
A
B
C
m
δ
ε
4) Но < δ+ <β+ < ε = 180°, СЛЕДОВАТЕЛЬНО:
< α+ <β+ < γ=180°
Климова Елизавета, лицей № 44, г. Липецк, E-mail: [e-mail]