Оценка качества показывает

Линейный коэффициент корреляции
Линейный коэффициент корреляции указывает, есть ли между двумя рядами X и Y линейная зависимость и какой силы. Вычисляется по следующей формуле:
mx , my , mxy — математическое ожидание x, y, xy:
Линейный коэффициент корреляции может иметь знак плюс или минус. Положительная его величина свидетельствует о прямой связи между X и Y. Чем ближе KR к +1, тем связь более тесная. Отрицательная величина его свидетельствует об обратной связи; в этом случае границей является –1. Близость KR к нулю свидетельствует о слабой связи между X и Y

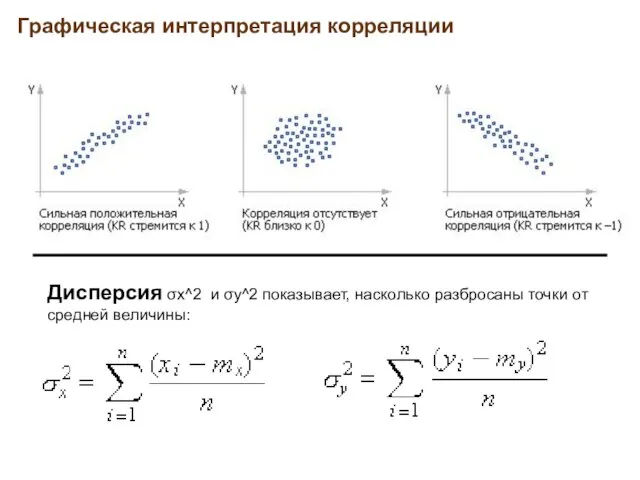
Графическая интерпретация корреляции
Дисперсия σx^2 и σy^2 показывает, насколько разбросаны точки от средней величины:

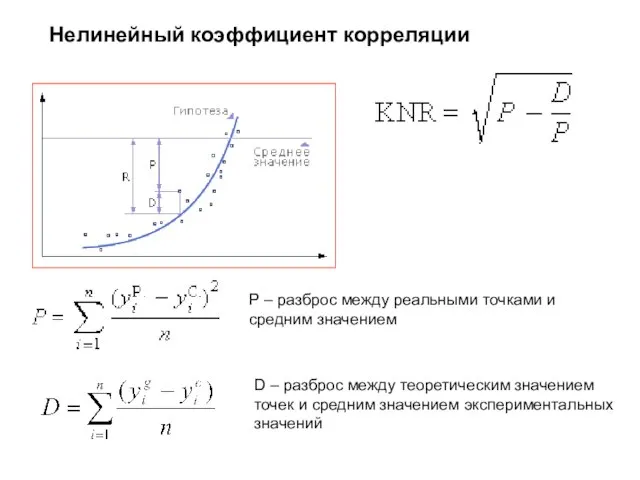
Нелинейный коэффициент корреляции
P – разброс между реальными точками и средним значением
D – разброс между теоретическим значением
точек и средним значением экспериментальных
значений

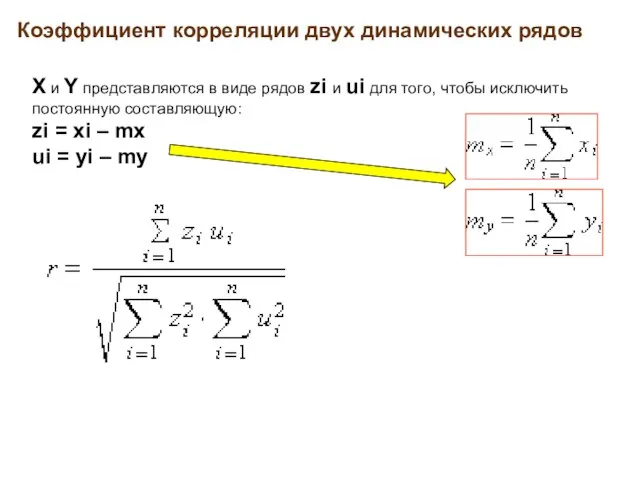
Коэффициент корреляции двух динамических рядов
X и Y представляются в виде рядов zi и ui для того, чтобы исключить постоянную составляющую:
zi = xi – mx
ui = yi – my

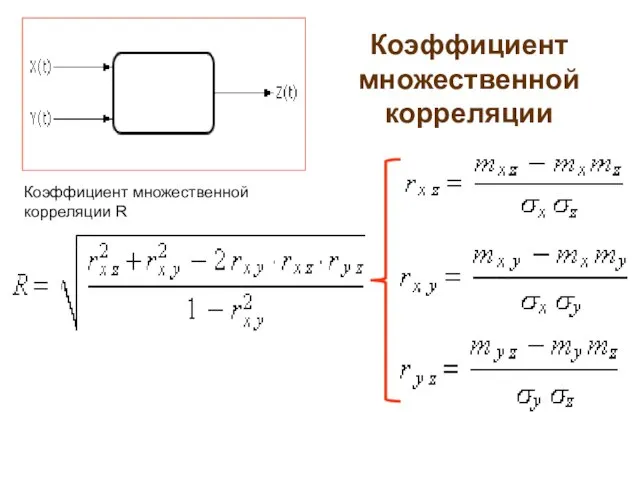
Коэффициент множественной корреляции
Коэффициент множественной корреляции R

Связь двух признаков
Коэффициент ассоциаций позволяет выяснить, имеется ли какая-либо связь между двумя признаками. Если данный коэффициент близок к единице, то в этом случае можно говорить о существовании такой связи.
Пример. Попытаемся с помощью данной формулы выяснить, есть ли связь между ростом и весом человека? Пусть в нашем распоряжении имеются данные о весе и росте 500 человек:
По формуле:
K = (304 · 67 – 17 · 112)/(304 · 67 + 17 · 112) = 0.83.
Так как величина 0.83 близка к 1, то можно говорить о существовании определенной связи между весом и ростом.